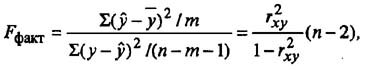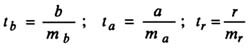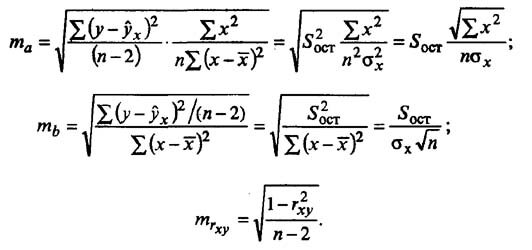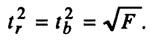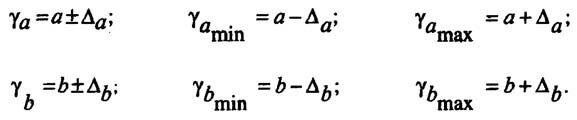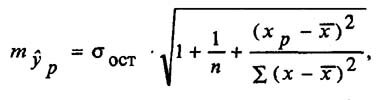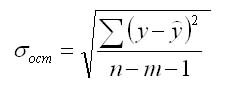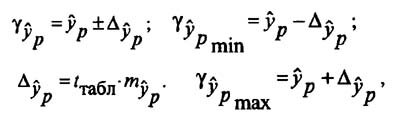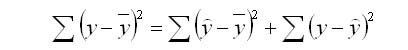Частный критерий фишера для уравнения множественной регрессии

Быстрая навигация по странице:

Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Понятие F-критерия Фишера

F-критерий Фишера – это один из важных статистических критериев, используемых при проверке значимости как уравнения регрессии в целом, так и отдельных его коэффициентов. Для оценки статистической значимости отдельных коэффициентов уравнения множественной регрессии используют так называемые частные F-критерий Фишера. Критическое значение данного критерия при проведении анализа определяется по специальным таблицам, а также может быть определено при помощи специальных функций в различных компьютерных программах. Например, в MS Excel для этого может быть использована функция FРАСПОБР.

Размещено на www.rnz.ru

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Формулы расчета F-критерия Фишера

В общем виде F-критерий Фишера рассчитывается по следующей формуле:

F = S 2 _факт / S 2 _ост;
где: S 2 _факт — факторная дисперсия;
S 2 _ост — остаточная дисперсия

Соответствующие виды дисперсий определяются по следующим формулам:

формула расчета факторной дисперсии

формула расчета остаточной дисперсии

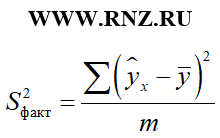
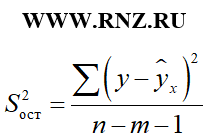
В приведенных формулах n – это число наблюдений, m – число параметров при переменной x (то есть количество факторов в модели регрессии).

При этом необходимо обратить внимание на то, что в зависимости от типа исследуемой модели регрессии применяемая формула определения F-критерия Фишера может изменяться. Например, для расчета F-критерия Фишера для парной линейной регрессии может использоваться следующая формула:

формула расчета F-критерия Фишера для парной линейной регрессии

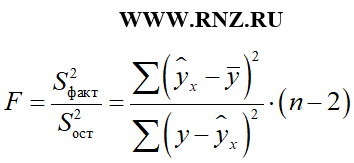
При использовании коэффициента детерминации расчет F-критерия Фишера для парной линейной регрессии может быть выполнен по такой формуле:

формула расчета F-критерия Фишера через коэффициент детерминации

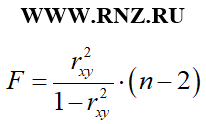
Для парной нелинейной модели регрессии расчет F-критерия Фишера может быть осуществлен через связь с индексом детерминации по следующей формуле:

формула расчета F-критерия Фишера для парной нелинейной модели регрессии через индекс детерминации

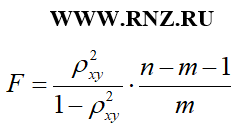
Описания параметров n и m приведено выше.

Для уравнения множественной регрессии F-критерий Фишера рассчитывается по следующей формуле:

формула расчета F-критерия Фишера для уравнения множественной регрессии

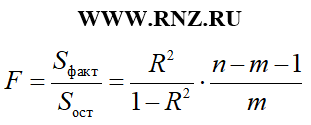
В процессе исследования уравнения множественной регрессии кроме общего F-критерий Фишера могут быть рассчитаны частные F-критерии. В случае анализа уравнения с двумя регрессорами (переменными) вычисление частных F-критериев может быть выполнено по следующим формулам:

формула расчета частных F-критериев Фишера для уравнения множественной регрессии

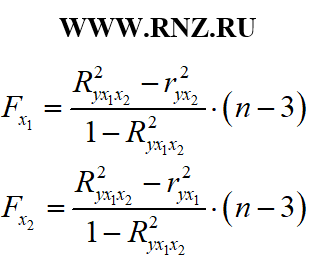
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Значимость F-критерия Фишера

Для определения статистической значимости рассчитанного значения F-критерия Фишера его сравнивают с критическим или табличным значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k₁; k₂), где k₁ = m – это количество факторов в построенной регрессионной модели, а k₂ = n – m – 1 (n – число наблюдений). Для частного F-критерия k₁ = 1, k₂ = n – m – 1 (n – число наблюдений).

Интерпретация F — критерия Фишера для уравнения регрессии в целом следующая: в том случае, когда фактическая величина F — критерия Фишера больше табличного показателя, то уравнение регрессии в целом является статистически значимым.

Интерпретация частного F — критерия Фишера следующая: в том случае, когда рассчитанная величина частного F_xi превышает критическое значение, то дополнительное включение фактора x_i в регрессионную модель статистически оправданно и коэффициент регрессии b_i при соответствующем факторе x_i статистически значим. Но если рассчитанная величина F_xi меньше табличного, то дополнительное включение в модель фактора x_i не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.

Видео:Проверка адекватности регрессии. Критерий ФишераСкачать

Пример расчета F-критерия Фишера

Приведем условные примеры расчета F-критерия Фишера

Пример №1. Предположим, что исследуется регрессия с одним фактором (парная), на основе 30-ти наблюдений, в которой коэффициент детерминации составил 0,77. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера составит: F = 0,77/(1-0,77)*(30-2) = 93,74. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 1; 30-1-1) = 4,2. Так как F > F_табл, то полученное уравнение регрессии является статистически значимым.

Пример №2. Предположим, что исследуется множественная регрессия с тремя факторами, на основе 40 наблюдений, в которой коэффициент множественной детерминации составил 0,89. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера для уравнения множественной регрессии составит: F = (0,89/(1-0,89))*((40-3-1)/3) = 97,09. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 3; 40-3-1) = 2,87. Так как F > F_табл, то полученное уравнение множественной регрессии является статистически значимым.

Видео:Расчет точного теста Фишера в excelСкачать

Онлайн-калькулятор F-критерия Фишера

Представляем онлайн калькулятор расчета F-критерия Фишера, используя который, Вы можете самостоятельно определить значения соответствующего показателя. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить и точно выполнить вычисления. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает и посмотреть, как правильно заполнять поля. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!

Калькулятор позволяет вычислить значение F-критерия Фишера на основе коэффициента детерминации (первый вариант) или на основе показателей сумм квадратов отклонений, т.е. используя элементы дисперсионного анализа. Выберите необходимый способ и выполните соответствующие вычисления. Для проверки статистической значимости используется уровень значимости α = 0.05.

Онлайн-калькулятор расчета значения F-критерия Фишера:

1-й вариант: на основе значения коэффициент (индекса) детерминации

2-й вариант: на основе сумм квадратов отклонений

Видео:Множественная регрессияСкачать

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;
m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Видео:Эконометрика. Линейная парная регрессияСкачать

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

1. Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
2. Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
3. На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Видео:Множественная регрессия в ExcelСкачать

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

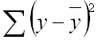
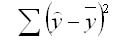
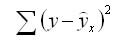
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

F-тест качества спецификации множественной регрессионной модели

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Рисунок 1 — простая линейная регрессия

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Рисунок 3

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

где n — число наблюдений, k — число независимых переменных.

Видео:A.4.14 Точный тест Фишера (введение в статистику)Скачать

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

где ,

,

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .

Масштабируем SSE и SSR с учетом их степеней свободы:

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе в случае линейной регрессионной модели вида (1).

Видео:Т-критерий Стьюдента за 12 минут. Биостатистика.Скачать

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Определим “полную” модель: (10)

Определим “укороченную” модель: (11)

Вычисляем сумму квадратов ошибок для каждой модели:

(12)

(13)

Определяем количество степеней свобод

(14)

Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

Из формулы (15) выразим SSE(F):

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

Видео:2.7. Распределение Хи квадрат, Стьюдента, Фишера .Скачать

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид . Следовательно. Используя формулу (14.в), получим

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501

📽️ Видео

12-05 Информация Фишера и свойства ММП оценокСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Множественная степенная регрессияСкачать

Математика #1 | Корреляция и регрессияСкачать