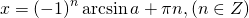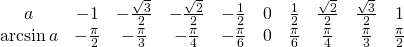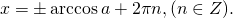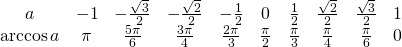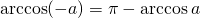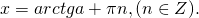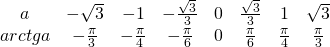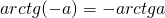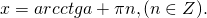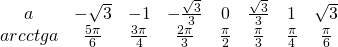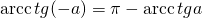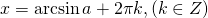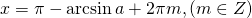Частные случаи тригонометрических уравнений арккосинус (5 видео)

Содержание

Узнать ещё
Формулы тригонометрических уравнений
21 комментарий на «Формулы тригонометрических уравнений»
Алгебра
Арккосинус
Решение уравнений tgx = a и ctgx = a
Тригонометрические уравнения — формулы, решения, примеры
Простейшие тригонометрические уравнения
Формулы корней тригонометрических уравнений в таблице
Методы решения тригонометрических уравнений
Алгебраический метод.
Разложение на множители.
Приведение к однородному уравнению
Переход к половинному углу
Введение вспомогательного угла
Дробно-рациональные тригонометрические уравнения
🎬 Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Формулы тригонометрических уравнений

Для удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице.

I. sin x =a

При │a│>1 это уравнение решений не имеет.

При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:

Таблица арксинусов

II. cos x=a

При │a│>1 это уравнение решений не имеет.

При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:

Таблица арккосинусов

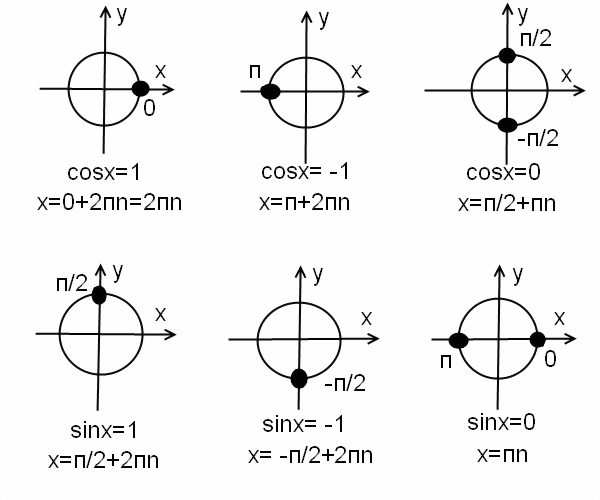
Частные случаи синуса и косинуса:

III. tg x=a

Уравнение имеет бесконечное множество решений при любых значениях a.

Таблица арктангенсов

IV. ctg x = a

Уравнение имеет бесконечное множество решений при любых значениях a.

Таблица арккотангенсов

21 комментарий на «Формулы тригонометрических уравнений»

Отличный сайт, спасибо, помог.

Спасибо за отличную оценку!
Я рада, что сайт Вам помог.

Пожалуйста!) Успехов Вам в учебе!

Сайт действительно хороший =)
Интересно, просто, ясно.
Спасибо Вам, Светлана Иванова!

Ариша, спасибо за теплый отзыв!

Опечатка в таблице арккотангенсов )
А так все отлично, хорошая статья

Опечатку исправила. Спасибо!

Не силен в этих науках и школу прогуливал всегда!Жалею теперь об этом!Но вот беда ума не могу приложить что может значить arccos0,932 что это?с чем его едят ?И как его посчитать!Смотрю на выше написанное и не пойму как мне это применить!Помгите убогому!

Антон, разобраться в математике можно в любом возрасте, было бы желание. Но придется потрудиться (а где без этого?).
arccos 0,932 — это такое число из промежутка [0;П], косинус которого равен 0,932.
Можно открыть таблицу Брадиса и найти угол, косинус которого равен этому числу: [0,932 approx cos ]Далее, если требуется ответ представить в радианах, градусы переводим в радианы. [pi = , Rightarrow = frac<>,][ = 21 cdot frac<> = frac<><>.]Отсюда [arccos 0,932 approx frac<><>.]
Если же arccos 0,932 появился в ходе решения тригонометрического уравнения — оставляйте его в таком виде.
Например:[cos x = 0,932][x = pm arccos 0,932 + 2pi n,n in Z.]Все, дальше ничего считать не надо (запись в таком виде — точное решение, а при нахождении арккосинуса ответ станет не точным, а приближенным. Поэтому его и не принято упрощать).

Светлана спасибо вам большое за помощь)Есть еще один вопросик я весь google перекопал. Какова единица измерения числа которое получается в результате вычисления cos или sin угла например sin47.376 градусов =0,735??какая единица измерения Arccos0,735=42.692. что это за величина и какая ее единица измерения?Голова дымит, а надо знать это,а то на работу не возьмут!

Косинус угла и синус угла — это просто число (в пределах от -1 до 1). Неважно, задан угол в градусах или в радианах.
Теперь — об арксинусах и арккосинусах. Если использовать таблицу Брадиса, arccos0,735 ищем как угол, косинус которого равен 0,735. [cos approx 0,735]То есть Ваши 42.692, насколько я понимаю, градусы. Но в градусах значения арккосинуса и арксинуса не оставляют. Нужно перевести в радианы. [ = 42 cdot frac<> = frac<><>.]7П/30 радиан, радианы не пишут. Радианная мера позволяет от градусной меры угла перейти к числам, чтобы потом графики тригонометрических функций в декартовой системе координат строить можно было, например.

Спасибо вы целиком и полностью удовлетворили мой интерес!

Спасибо за шпору =), пошел сдавать

Ещё о таблицах. Точнее их отсутствии…
на калькуляторе мы получаем cos, затем arccos. Верно ли я понимаю, что значения arccos вычисляются в радианной мере, и после этого следует обязательно перевести в градусную меру? (Таблицы Брадиса, также как и любые другие, идут уже (!) с перерасчетом радианов в градусы. ) …но таблиц нет, к примеру. Некоторые on-line–научные калькуляторы имеют опцию переключения с градусов в радианы и/или наоборот; при этом по умолчанию может стоять опция (галочка) как радианной меры, так и градусной.
Вопрос: в каких случаях надобно переходить с радианов в градусы?
(функции MS Office Excel, например, предусматривают именно трёхстадийный процесс вычисления: cos, arccos, затем перевод радианов в градусы).
И ещё вопросик: Таблицы содержат значения синусов/косинусов только для острых углов в ПРЯМОУГОЛЬНОМ треугольнике?
Пример, имеется равносторонний треугольник (все стороны и углы равны), нам надо найти угол (мы его не знаем). Сторона (все три стороны равны) = 60 см. Т.е. поделив все [равные] стороны получим
sin = cos = tg = ctg = sec = cosec = 1
но по этому значению угол [каковой реально 60°] найти в таблицах невозможно. Спасибо!

Nick, прошу прощения, что затянула с ответом. Меня мучает совесть(
С калькулятором я практически не работаю, предпочитаю считать либо устно, либо письменно. Если нужно, пользуюсь таблицами Брадиса. Над нюансами вычислений с калькулятором не задумывалась.
Значения синуса и косинуса зависят только от угла, но не от вида треугольника. Мы вводим определение синуса в прямоугольном треугольнике как отношение противолежащего катета к гипотенузе, потом расширяем определение, называя синусом угла альфа ординату точки единичной окружности, полученной из точки (1;0) поворотом на угол альфа.
Синус угла в произвольном треугольнике можно найти посредством через теорему синусов, через площадь треугольника (из формулы S=1/2 ab sin α), или провести высоту и рассмотреть прямоугольный треугольник.
В таблице Брадиса значения тригонометрических функций даны только для острых углов. Для тупых углов значения находят с помошью формул приведения.

Объясните мне, пожалуйста, если п принадлежит Z, где п — , Z — .я не могу понять когда п четное, п — нечетное и что такое Z?

Тамара, семейство решений для общего случая уравнений sinx=a

можно разбить на два семейства решений:
1) при n=2k (то есть для чётных)

2) при n=2m+1 (то есть для нечётных)

Z — множество целых чисел, то есть 0; ±1; ±2; ±3; …

Страница интересная,но я не нашла частные случаи для тангенса и котангенса.Помогите пожалуйста(очень нужно

Евгения, формул частных случаем для тангенса и котангенса нет. Иногда частными случаями называют уравнения вида tgx=1; tgx=-1; ctgx=1; ctgx=-1, но общая формула верна и для каждого из этих случаев.

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Алгебра

План урока:

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Арккосинус

Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:

Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.

Задание. Решите ур-ние

Задание. Запишите корни ур-ния

Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.

Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:

Ответ: 7π/3 и 8π/3.

Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние

Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:

Наконец, решениями ур-ния

Видео:Тригонометрические уравнения (Частные случаи)Скачать

Решение уравнений tgx = a и ctgx = a

Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):

Таким образом, у ур-ния tgx = a существует очевидное решение

Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:

Задание. Решите ур-ние

Задание. Запишите формулу корней ур-ния

Далее рассмотрим ур-ние вида

Задание. Решите ур-ние

Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии

Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Тригонометрические уравнения — формулы, решения, примеры

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Простейшие тригонометрические уравнения

Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.

1. Уравнение `sin x=a`.

При `|a|>1` не имеет решений.

При `|a| leq 1` имеет бесконечное число решений.

Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| leq 1` имеет бесконечное множество решений.

Формула корней: `x=pm arccos a + 2pi n, n in Z`

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + pi n, n in Z`

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + pi n, n in Z`

Видео:Тригонометрические уравнения. Частные случаи для синуса и косинуса.Скачать

Формулы корней тригонометрических уравнений в таблице

Для синуса:Для косинуса:Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

с помощью тригонометрических формул преобразовать его до простейшего;
решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.

Рассмотрим на примерах основные методы решения.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`

Решение. Используя формулы приведения, имеем:

`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,

делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,

находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:

1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.

2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.

Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.

Разложение на множители.

Пример. Решить уравнение: `sin x+cos x=1`.

Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

`sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
`cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.

Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.

Приведение к однородному уравнению

Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:

`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).

Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.

Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.

Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:

`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда: