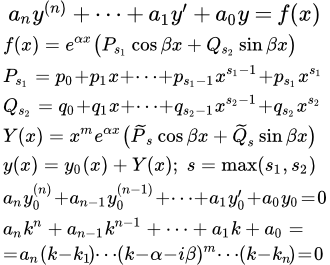Частное решение уравнения вида где правая часть многочлен первой степени следует искать в виде

Видео:Видеоурок "Нахождение частных решений по виду правой части"Скачать

Пример частного решения линейного дифференциального уравнения

Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C’₁·e -3x ·cos(2x)+C’₂·e -3x ·sin(2x)=0
C’₁(-2·e -3x ·sin(2x)-3·cos(2x)·e -3x ) + C’₂(-3·e -3x ·sin(2x)+2·cos(2x)·e -3x ) = 8*exp(-x)
Выразим C’₁ из первого уравнения:
C’₁ = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’₁ = -4·e 2x ·sin(2x)
C’₂ = 4·cos(2x)·e 2x
Интегрируем полученные функции C’_i:
C₁ = -e 2x ·sin(2x)+cos(2x)·e 2x + C * ₁
C₂ = e 2x ·sin(2x)+cos(2x)·e 2x + C * ₂
Записываем полученные выражения в виде:
C₁ = (-e 2x ·sin(2x)+cos(2x)·e 2x )·cos(2x)·e -3x + C * ₁e -3x ·cos(2x)
C₂ = (e 2x ·sin(2x)+cos(2x)·e 2x )·e -3x ·sin(2x) + C * ₂e -3x ·sin(2x)
или
C₁ = -cos(2x)·e -x ·sin(2x)+cos 2 (2x)·e -x + C * ₁e -3x ·cos(2x)
C₂ = cos(2x)·e -x ·sin(2x)+sin 2 (2x)·e -x + C * ₂e -3x ·sin(2x)
y = C₁ + C₂
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример . y″ + 5y’ + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r 2 +5 r + 6 = 0
Находим дискриминант: D = 5 2 — 4·1·6 = 1


Корни характеристического уравнения: r₁ = -2, r₂ = -3. Следовательно, фундаментальную систему решений составляют функции: y₁ = e -2x , y₂ = e -3x
Общее решение однородного уравнения имеет вид: y =C₁·e -2x +C₂·e -3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c₁+c2, то получаем первое уравнение:
c₁+c2 = 1
Находим первую производную: y’ = -3·c₂·e -3·x -2·c1·e -2·x
Поскольку y'(0) = -3·c₂-2·c₂, то получаем второе уравнение:
-3·c₂-2·c₂ = 3
В итоге получаем систему из двух уравнений:
c₁+c2 = 1
-3·c₂-2·c₂ = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c₁ = 6, c₂ = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y =6·e -2x -5·e -3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3 /₁₃;B = 15 /₁₃;
Частное решение имеет вид:
y * = 3 /₁₃cos(2x) + 15 /₁₃sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 2 . y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r 2 + 1 = 0
D = 0 2 — 4·1·1 = -4

Корни характеристического уравнения:
(комплексные корни):
r₁ = i, r₂ = -i
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 0 x cos(x) = cos(x)
y₂ = e 0 x sin(x) = sin(x)

Общее решение однородного уравнения имеет вид: y =C₁·cos(x)+C₂·sin(x)

Рассмотрим правую часть: f(x) = cos(x)

Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r₁).

Уравнение имеет частное решение вида:
y * = x (Acos(x) + Bsin(x))
Вычисляем производные:
y’ = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1 /₂;
Частное решение имеет вид: y * = x (0cos(x) + ½ sin(x)) = ½ x sin(x)

Таким образом, общее решение дифференциального уравнения имеет вид:

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Видео:Деление многочлена на многочленСкачать

Определение общего решения по известному частному решению

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Видео:Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Вначале ищем общее решение однородного уравнения:
(3) .

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Видео:Метод неопределенных коэффициентов для линейного ДУ со специальной правой частью (квазимногочленом)Скачать

Установление вида частного решения

Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .

Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .

Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .

Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).

Если среди корней характеристического уравнения (4) есть корень кратности p со значением

то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Частные случаи

Неоднородность в виде многочлена

Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.

Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020

Видео:Суперпозиция частных решений линейного неоднородного дифференциального уравненияСкачать

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.

Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y » + p · y ‘ + q · y = f ( x ) , где произвольными числами являются p и q , а имеющаяся функция f ( х ) непрерывная на интервале интегрирования x .

Перейдем к формулировке теоремы общего решения ЛНДУ.

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Теорема общего решения ЛДНУ

Общим решением, находящимся на интервале х , неоднородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = f ( x ) с непрерывными коэффициентами интегрирования на x интервале f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функцией f ( x ) равняется сумме общего решения y 0 , которое соответствует ЛОДУ и каким-нибудь частным решением y

, где исходным неоднородным уравнением является y = y 0 + y

Отсюда видно, что решение такого уравнения второго порядка имеет вид y = y 0 + y

. Алгоритм нахождения y 0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y

Выбор частного решения ЛНДУ зависит от вида имеющейся функции f ( x ) , располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.

Когда f ( x ) считается за многочлен n -ой степени f ( x ) = P n ( x ) , отсюда следует, что частное решение ЛНДУ находим по формуле вида y

= Q n ( x ) · x γ , где Q n ( x ) является многочленом степени n , r – это количество нулевых корней характеристического уравнения. Значение y

является частным решением y

= f ( x ) , тогда имеющиеся коэффициенты, которые определены многочленом
Q n ( x ) , отыскиваем при помощи метода неопределенных коэффициентов из равенства y

Вычислить по теореме Коши y » — 2 y ‘ = x 2 + 1 , y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .

Решение

Иначе говоря, необходимо перейти к частному решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y » — 2 y ‘ = x 2 + 1 , которое будет удовлетворять заданным условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .

Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y 0 или частному решению неоднородного уравнения y

, то есть y = y 0 + y

Для начала найдем общее решение для ЛНДУ, а после чего – частное.

Перейдем к нахождению y 0 . Запись характеристического уравнения поможет найти корни. Получаем, что

k 2 — 2 k = 0 k ( k — 2 ) = 0 k 1 = 0 , k 2 = 2

Получили, что корни различные и действительные. Поэтому запишем

y 0 = C 1 e 0 x + C 2 e 2 x = C 1 + C 2 e 2 x .

. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y

= Q 2 ( x ) · x γ = ( A x 2 + B x + C ) · x = A x 3 + B x 2 + C x , где значения А , В , С принимают неопределенные коэффициенты.

Найдем их из равенства вида y

Тогда получим, что:

‘ = x 2 + 1 ( A x 3 + B x 2 + C x ) » — 2 ( A x 3 + B x 2 + C x ) ‘ = x 2 + 1 3 A x 2 + 2 B x + C ‘ — 6 A x 2 — 4 B x — 2 C = x 2 + 1 6 A x + 2 B — 6 A x 2 — 4 B x — 2 C = x 2 + 1 — 6 A x 2 + x ( 6 A — 4 B ) + 2 B — 2 C = x 2 + 1

Приравняв коэффициенты с одинаковыми показателями степеней x , получим систему линейных выражений — 6 A = 1 6 A — 4 B = 0 2 B — 2 C = 1 . При решении любым из способов найдем коэффициенты и запишем: A = — 1 6 , B = — 1 4 , C = — 3 4 и y

= A x 3 + B x 2 + C x = — 1 6 x 3 — 1 4 x 2 — 3 4 x .

Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Для нахождения частного решения, которое удовлетворяет условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 , требуется определить значения C 1 и C 2 , исходя из равенства вида y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .

y ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x x = 0 = C 1 + C 2 y ‘ ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x ‘ x = 0 = = 2 C 2 e 2 x — 1 2 x 2 + 1 2 x + 3 4 x = 0 = 2 C 2 — 3 4

Работаем с полученной системой уравнений вида C 1 + C 2 = 2 2 C 2 — 3 4 = 1 4 , где C 1 = 3 2 , C 2 = 1 2 .

Применив теорему Коши, имеем, что

y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x = = 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x

Ответ: 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .

Когда функция f ( x ) представляется в виде произведения многочлена со степенью n и экспоненты f ( x ) = P n ( x ) · e a x , тогда отсюда получаем, что частным решением ЛНДУ второго порядка будет уравнение вида y

= e a x · Q n ( x ) · x γ , где Q n ( x ) является многочленом n -ой степени, а r – количеством корней характеристического уравнения, равняющиеся α .

Коэффициенты, принадлежащие Q n ( x ) находятся по равенству y

Найти общее решение дифференциального уравнения вида y » — 2 y ‘ = ( x 2 + 1 ) · e x .

Решение

Уравнение общего вида y = y 0 + y

. Указанное уравнение соответствует ЛОДУ y » — 2 y ‘ = 0 . По предыдущему примеру видно, что его корни равняются k 1 = 0 и k 2 = 2 и y 0 = C 1 + C 2 e 2 x по характеристическому уравнению.

Видно, что правой частью уравнения является x 2 + 1 · e x . Отсюда ЛНДУ находится через y

= e a x · Q n ( x ) · x γ , где Q n ( x ) , являющимся многочленом второй степени, где α = 1 и r = 0 , потому как у характеристического уравнения отсутствует корень, равный 1 . Отсюда получаем, что

= e a x · Q n ( x ) · x γ = e x · A x 2 + B x + C · x 0 = e x · A x 2 + B x + C .

А , В , С являются неизвестными коэффициентами, которые можно найти по равенству y

‘ = e x · A x 2 + B x + C ‘ = e x · A x 2 + B x + C + e x · 2 A x + B = = e x · A x 2 + x 2 A + B + B + C y

‘ ‘ = e x · A x 2 + x 2 A + B + B + C ‘ = = e x · A x 2 + x 2 A + B + B + C + e x · 2 A x + 2 A + B = = e x · A x 2 + x 4 A + B + 2 A + 2 B + C

‘ = ( x 2 + 1 ) · e x ⇔ e x · A x 2 + x 4 A + B + 2 A + 2 B + C — — 2 e x · A x 2 + x 2 A + B + B + C = x 2 + 1 · e x ⇔ e x · — A x 2 — B x + 2 A — C = ( x 2 + 1 ) · e x ⇔ — A x 2 — B x + 2 A — C = x 2 + 1 ⇔ — A x 2 — B x + 2 A — C = 1 · x 2 + 0 · x + 1

Показатели при одинаковых коэффициентах приравниваем и получаем систему линейных уравнений. Отсюда и находим А , В , С :

— A = 1 — B = 0 2 A — C = 1 ⇔ A = — 1 B = 0 C = — 3

Ответ: видно, что y

= e x · ( A x 2 + B x + C ) = e x · — x 2 + 0 · x — 3 = — e x · x 2 + 3 является частным решением ЛНДУ, а y = y 0 + y = C 1 e 2 x — e x · x 2 + 3 — общим решением для неоднородного дифуравнения второго порядка.

Когда функция записывается как f ( x ) = A 1 cos ( β x ) + B 1 sin β x , а А 1 и В 1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y

= A cos β x + B sin β x · x γ , где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ± i β . В этом случае поиск коэффициентов проводится по равенству y

Найти общее решение дифференциального уравнения вида y » + 4 y = cos ( 2 x ) + 3 sin ( 2 x ) .

Решение

Перед написанием характеристического уравнения находим y 0 . Тогда

k 2 + 4 = 0 k 2 = — 4 k 1 = 2 i , k 2 = — 2 i

Имеем пару комплексно сопряженных корней. Преобразуем и получим:

y 0 = e 0 · ( C 1 cos ( 2 x ) + C 2 sin ( 2 x ) ) = C 1 cos 2 x + C 2 sin ( 2 x )

Корни из характеристического уравнения считаются сопряженной парой ± 2 i , тогда f ( x ) = cos ( 2 x ) + 3 sin ( 2 x ) . Отсюда видно, что поиск y

будет производиться из y

= ( A cos ( β x ) + B sin ( β x ) · x γ = ( A cos ( 2 x ) + B sin ( 2 x ) ) · x . Неизвестные коэффициенты А и В будем искать из равенства вида y

= cos ( 2 x ) + 3 sin ( 2 x ) .

‘ = ( ( A cos ( 2 x ) + B sin ( 2 x ) · x ) ‘ = = ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) y

» = ( ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) ) ‘ = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) — — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x )

Тогда видно, что

= cos ( 2 x ) + 3 sin ( 2 x ) ⇔ ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) + + 4 ( A cos ( 2 x ) + B sin ( 2 x ) ) · x = cos ( 2 x ) + 3 sin ( 2 x ) ⇔ — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) = cos ( 2 x ) + 3 sin ( 2 x )

Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:

— 4 A = 3 4 B = 1 ⇔ A = — 3 4 B = 1 4

= ( A cos ( 2 x ) + B sin ( 2 x ) · x = — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x .

Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается

= = C 1 cos ( 2 x ) + C 2 sin ( 2 x ) + — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x

Когда f ( x ) = e a x · P n ( x ) sin ( β x ) + Q k ( x ) cos ( β x ) , тогда y

= e a x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ . Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α ± i β , где P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , т , m , где m = m a x ( n , k ) . Нахождение коэффициентов L m ( x ) и N m ( x ) производится, исходя из равенства y

Найти общее решение y » + 3 y ‘ + 2 y = — e 3 x · ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) .

Решение

По условию видно, что

α = 3 , β = 5 , P n ( x ) = — 38 x — 45 , Q k ( x ) = — 8 x + 5 , n = 1 , k = 1

Тогда m = m a x ( n , k ) = 1 . Производим нахождение y 0 , предварительно записав характеристическое уравнение вида:

k 2 — 3 k + 2 = 0 D = 3 2 — 4 · 1 · 2 = 1 k 1 = 3 — 1 2 = 1 , k 2 = 3 + 1 2 = 2

Получили, что корни являются действительными и различными. Отсюда y 0 = C 1 e x + C 2 e 2 x . Далее необходимо искать общее решение, исходя из неоднородного уравнения y

= e α x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) · x 0 = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) )

Известно, что А , В , С являются коэффициентами, r = 0 , потому как отсутствует пара сопряженных корней, относящихся к характеристическому уравнению с α ± i β = 3 ± 5 · i . Данные коэффициенты находим из полученного равенства:

= — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) ⇔ ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) » — — 3 ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) = — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) )

Нахождение производной и подобных слагаемых дает

— e 3 x · ( ( 15 A + 23 C ) · x · sin ( 5 x ) + + ( 10 A + 15 B — 3 C + 23 D ) · sin ( 5 x ) + + ( 23 A — 15 C ) · x · cos ( 5 x ) + ( — 3 A + 23 B — 10 C — 15 D ) · cos ( 5 x ) ) = = — e 3 x · ( 38 · x · sin ( 5 x ) + 45 · sin ( 5 x ) + + 8 · x · cos ( 5 x ) — 5 · cos ( 5 x ) )

После приравнивания коэффициентов получаем систему вида

15 A + 23 C = 38 10 A + 15 B — 3 C + 23 D = 45 23 A — 15 C = 8 — 3 A + 23 B — 10 C — 15 D = — 5 ⇔ A = 1 B = 1 C = 1 D = 1

Из всего следует, что

= e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) = = e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Ответ: теперь получено общее решение заданного линейного уравнения:

= = C 1 e x + C 2 e 2 x + e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Видео:Деление многочленов | Математика | TutorOnlineСкачать

Алгоритм решения ЛДНУ

Любой другой вид функции f ( x ) для решения предусматривает соблюдение алгоритма решения:

• нахождение общего решения соответствующего линейного однородного уравнения, где y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 являются линейно независимыми частными решениями ЛОДУ, С 1 и С 2 считаются произвольными постоянными;
• принятие в качестве общего решения ЛНДУ y = C 1 ( x ) ⋅ y 1 + C 2 ( x ) ⋅ y 2 ;
• определение производных функции через систему вида C 1 ‘ ( x ) + y 1 ( x ) + C 2 ‘ ( x ) · y 2 ( x ) = 0 C 1 ‘ ( x ) + y 1 ‘ ( x ) + C 2 ‘ ( x ) · y 2 ‘ ( x ) = f ( x ) , а нахождение функций C 1 ( x ) и C 2 ( x ) посредствам интегрирования.

Найти общее решение для y » + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x .

Решение

Переходим к написанию характеристического уравнения, предварительно записав y 0 , y » + 36 y = 0 . Запишем и решим:

k 2 + 36 = 0 k 1 = 6 i , k 2 = — 6 i ⇒ y 0 = C 1 cos ( 6 x ) + C 2 sin ( 6 x ) ⇒ y 1 ( x ) = cos ( 6 x ) , y 2 ( x ) = sin ( 6 x )

Имеем, что запись общего решения заданного уравнения получит вид y = C 1 ( x ) · cos ( 6 x ) + C 2 ( x ) · sin ( 6 x ) . Необходимо перейти к определению производных функций C 1 ( x ) и C 2 ( x ) по системе с уравнениями:

C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) · ( cos ( 6 x ) ) ‘ + C 2 ‘ ( x ) · ( sin ( 6 x ) ) ‘ = 0 ⇔ C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) ( — 6 sin ( 6 x ) + C 2 ‘ ( x ) ( 6 cos ( 6 x ) ) = = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Необходимо произвести решение относительно C 1 ‘ ( x ) и C 2 ‘ ( x ) при помощи любого способа. Тогда запишем:

C 1 ‘ ( x ) = — 4 sin 2 ( 6 x ) + 2 sin ( 6 x ) cos ( 6 x ) — 6 e 6 x sin ( 6 x ) C 2 ‘ ( x ) = 4 sin ( 6 x ) cos ( 6 x ) — 2 cos 2 ( 6 x ) + 6 e 6 x cos ( 6 x )

Каждое из уравнений следует проинтегрировать . Тогда запишем получившиеся уравнения:

C 1 ( x ) = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 C 2 ( x ) = — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4

Отсюда следует, что общее решение будет иметь вид:

y = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 · cos ( 6 x ) + + — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4 · sin ( 6 x ) = = — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )

Ответ: y = y 0 + y

= — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )

🎥 Видео

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Нахождение вида частных решений ЛНДУСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Как проверяют учеников перед ЕНТСкачать

Линейные неоднородные ДУ с правой частью специального вида | Лекция 11 | Математика: Диффуры | СтримСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Пример 1 решения ЛНДУСкачать

ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

2214 ЛНДУ. Правая часть - многочлен, среди корней характеристического уравнения нет нулей.Скачать

Решение матричных уравненийСкачать