| Название | V011. Кинематика поступательного движения м т |
| Дата | 18.06.2018 |
| Размер | 0.86 Mb. |
| Формат файла |  |
| Имя файла | Baza_NTK.docx |
| Тип | Документы #47211 |
| страница | 3 из 6 |
| Подборка по базе: І. Кинематика Механикалы_ _оз_алыс. Механиканы_ негізгі есебі. М, Волонтерские движения в спорте..pdf, 11111Викторины для школьников по правилам дорожного движения.doc, Роботтың динамикасы мен кинематикасы.docx, Порядок ограждения мест внезапно возникшего препятствия для движ, Алексеенко В.А., Копанев М.В., Целищев В.А._Синтез и анализ комб, Маршрут движения.docx, 6 Анализ движения денежных потоков.doc, ИДЗ Механика поступательного и вращательного движения.docx, 1.1 Кинематика точки.pdf Содержание
Видео:Урок 89. Движение по окружности (ч.1)Скачать  задачи1. Вектор, равный по модулю углу поворота твердого тела и направленный вдоль оси вращения, называется … перемещением тела. 2. Направление вектора углового перемещения тела связано с направлением вращения тела правилом … буравчика. 3. При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при любом характере вращения сонаправленными будут векторы 1) 2) 3) 4) все вектора направлены одинаково при любом движении 4. При вращательном движении тела вокруг оси, кинематическими характеристиками движения являются 1) 2) 3) 5.Вектор угловой скорости материальной точки определяется формулой 1) 6. Вектор углового ускорения материальной точки определяется формулой 1) 2) 3) 4) 7. Частица движется по окружности, ее угловая скорость меняется в соответствии с уравнением 8. Проекция угловой скорости тела на ось вращения зависит от времени согласно уравнению 9. Частица движется по окружности, в соответствии с уравнением 10. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Уравнение, верно отражающее зависимость угловой скорости от времени, имеет вид 1) 3) 11. На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, по окружности, от времени t. Уравнение, верно отражающее представленную зависимость, имеет вид 1) 4) 12. На графике представлена зависимость (парабола) угла поворота φ тела, вращающегося вокруг неподвижной оси, от времени t. Про характер движения рассматриваемого тела можно утверждать, что оно вращается 1) равноускоренно с начальной скоростью равной нулю 2) равноускоренно с отличной от нуля начальной скоростью 3) равнозамедленно с конечной скоростью равной нулю 13. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. До остановки тело повернется на угол, равный … рад. (с округлением до десятых долей). 14. На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Модуль углового ускорения равен … рад/с 2 (с округлением до десятых долей). 15. Модуль угловой скорости точки, движущейся по окружности, изменяется с течением времени так, как показано на графике. Угол между векторами полного ускорения 1) увеличивается 2) уменьшается 3) не изменяется V 021. Законы Ньютона 1. Скорость тела не изменяется, если векторная сумма действующих на него сил равна нулю. Этот закон справедлив … 1 ) всегда 2) только в инерциальных системах отсчёта 3) только в системах отсчёта, неподвижных относительно Земли 4) только в системах отсчёта, неподвижных относительно Солнца 2. Падение тела на Землю рассматривается относительно трёх систем отсчёта. Телами отсчёта в этих системах являются а) планета Земля; б) автомобиль, движущийся равномерно и прямолинейно; в) самолёт, стартующий с аэродрома. Ускорение падающего тела будет одинаково в системах отсчета 1) а, б, в 2) а, б 3) а, в 4) б, в :2 3. При движении тел всегда совпадают по направлению два вектора 1) 4. .При переходе от одной ИСО к другой не изменяется численное значение величины 1) скорость 2) путь 3) перемещение 4) ускорение :4 5. На материальную точку действуют силы. Эта точка может: 1) двигаться с постоянной скоростью, если сумма всех действующих на неё сил не равна нулю 2) изменять направление своего движения относительно выбранной инерциальной системы отсчёта 3) двигаться с ускорением 4) покоиться относительно выбранной инерциальной системы отсчёта 6. На тело действуют две силы, обозначенные на рисунке векторами 1 и 3. Вектор ускорения тела совпадает с направлением вектора, обозначенного цифрой … 7. На покоящуюся точку начинают действовать четыре силы 1) в направлении силы 2) в направлении силы 3) в направлении силы 4) в направлении силы 5) остается в покое 8. На тело массы m действует сила 1) увеличится в 2 раза 2) увеличится в 4 раза 3) уменьшится в 2 раза 4) не изменится 9. На рис.1 показано направление вектора скорости v и ускорения a движущегося тела. Направление равнодействующей всех сил, действующих на тело, на рис.2 совпадает с направлением … :3 10. Величина равнодействующей двух равных по модулю сил F1 = F2 = 5,0 Н, направленных под углом 60 о друг к другу, равна … Н. 1) 5,0 2) 5 √3 3) 10 4) 7,0 :2 11. Тело, подвешенное на нити, совершает свободные колебания в вертикальной плоскости. Тангенциальное ускорение тела равно нулю, когда тело находится в положении … 12. . На рисунке изображен график зависимости проекции скорости Vх от времени для движущегося тела. Суммарная сила, действующая на это тело со стороны других тел, имеет максимальное значение на интервале времени 13. На рис.1 показаны вектора суммарной силы, действующей на тело, и скорости тела в некоторый момент времени. Направление ускорения этого тела совпадает с направлением вектора с номером … на рис 2. :1 14. Верное утверждение о направлениях скорости тела, его ускорения и суммарной силы, действующей на него, – 1) ускорение и сила всегда совпадают по направлению, а скорость может не совпадать 2) скорость, ускорение и сила всегда совпадают по направлению. 3) ускорение и сила всегда совпадают по направлению, а скорость направлена противоположно им 4) скорость и сила всегда совпадают по направлению, а ускорение направлено противоположно им 15. Тело массой m движется прямолинейно вдоль оси Ох. Движению тела под действием постоянной силы соответствует график номер … 16. Для сил, с которыми действуют друг на друга два взаимодействующих тела, справедливо утверждение 1) они равны по модулю и одинаково направлены 2) они равны по модулю и противоположно направлены 3) они различны по модулю и одинаково направлены 4) они различны по модулю и противоположны по направлению 17. На рисунке представлен график зависимости проекции ускорения аX от времени t для материальной точки, движущейся вдоль оси OX. На точку действовала постоянная сила, имеющая положительную проекцию на ось ОХ, на участке под номером 1) 1 2) 2 3) 3 4) 4 5) 5 18. Тело покоится на горизонтальной опоре. На рисунке показаны силы, действующие на тело и на опору. Третьим законом Ньютона связана пара сил 1) 19. Тело движется по гладкой горизонтальной поверхности. Пара сил, входящих в третий закон Ньютона, 1) 20. Тело находится в равновесии на наклонной плоскости. На рисунке показаны силы, действующие на тело и на опору. Третьим законом Ньютона связана пара сил 1) 4) ни одна из приведенных пар :2 21. Тело скользит с ускорением а вниз по наклонной плоскости с углом наклона к горизонту. Коэффициенту трения скольжения соответствует выражение 1) 22. Теннисный мяч летел с импульсом 1) вниз 2) вверх 3) вправо 4) влево :2 23. Два шара имеющие массы m1 и m2 действуют друг на друга с силами :2 2.На рисунке изображены графики зависимости силы F, действующей на материальную точку, от пройденного пути S. Сила F совершает одинаковую работу в случаях, приведенных под номерами 1) 1 и 2 3. На рисунке изображен график зависимости от времени работы, которую совершила над материальной точкой действующая на нее сила. Мощность этой силы обращалась в нуль в момент(ы) времени 1) 4. На рисунке изображен график зависимости от времени работы, которую совершила над материальной точкой действующая на нее сила. Кривая представляет собой параболу. Про модуль и знак мощности можно утверждать следующее: от 0 до 1) от 0 до 2) от 0 до 3) от 0 до 4) от 0 до 5) от 5. На рисунке указаны направления результирующей силы 6. На рисунке указаны направления результирующей силы 7. На рисунке изображены графики зависимости проекций сил на направление движения от пройденного пути. Максимальные значения 1) 1 и 3 2) 2 и 4 3) 2 и 3 4) 1 и 4 :2 8. На рисунке представлен график зависимости модуля силы 9. Материальная точка движется вдоль оси ОХ согласно уравнению 17. На рисунке изображен график зависимости от времениt. работы, которую совершила над материальной точкой действующая на нее сила. Верными являются утверждения: 1) мощность этой силы изменялась по модулю 2) мощность этой силы не изменялась по знаку 3) мощность этой силы обращалась в нуль на указанном интервале времени 4) траектория точки могла быть замкнутой за изображенный на рисунке промежуток времени 18. Тело движется по оси ОХ под действием силы, зависимость проекции которой от координаты х представлена на рисунке. Работа силы на пути 1) 19. Тело движется по оси ОХ под действием силы, зависимость проекции которой на ось ОХ от времениt представлена на рисунке. Мощность силы будет положительной и максимальной по модулю на интервале времени … 20. Две материальные точки aиb движутся вдоль оси Ох. На рисунке изображены графики зависимостей их координат от времени. Кинетическая энергия этих точек …… 1) для точки а — увеличивается 2) для точки а — не изменяется, 3) для точки а — уменьшается 4) для точки b – уменьшается 5) для точки b – увеличивается 6) для точки b — не изменяется 1.Для кинетической энергии НЕСПРАВЕДЛИВЫМ является утверждение 1) изменение кинетической энергии обусловлено работой консервативных и неконсервативных сил 2) кинетическая энергия зависит от скорости, с которой движется тело 3) кинетическая энергия является функцией координат 4) кинетическая энергия всегда положительна или равна нулю :3 2. Для кинетической энергии справедливыми являются утверждения: кинетическая энергия 1) является функцией механического состояния тела, т.е. ее приращение не зависит от пути (способа) перехода тела из одного состояния в другое, а определяется только механическими параметрами этих состояний 2) является величиной аддитивной, т.е. кинетическая энергия системы частиц равна сумме кинетических энергий этих частиц 3) является величиной инвариантной, т.е. сохраняется неизменным ее числовое значение при переходе от одной системы отсчета к другой 4) точки увеличивается, если над материальной точкой совершается положительная по знаку работа :1,2,4 3. Для потенциальной энергии справедливыми являются утверждения: 1) потенциальная энергия является функцией координат взаимодействующих тел (расстояния между ними) 2) модуль и знак потенциальной энергии зависят от выбора нулевого уровня потенциальной энергии, т.е. такого относительного расположения тел, при котором их потенциальную энергию полагают равной нулю 3) потенциальная энергия зависит (в классической механике) от выбора системы отсчета 4) убыль потенциальной энергии равна работе только консервативных сил, которые обусловливают эту энергию :1,2,4 4. Для потенциальной энергии НЕСПРАВЕДЛИВЫМ является утверждение 1) потенциальная энергия является функцией расстояния между взаимодействующими телами 2) потенциальная энергия не может быть отрицательной 3) убыль потенциальной энергии равна работе, совершаемой консервативными силами 4) численное значение потенциальной энергии не зависит от выбора системы отсчета. :2 5. Механическая система замкнута и неконсервативна. Верными являются утверждения: 1) векторная сумма всех внутренних сил, действующих в этой системе равна нулю 2) механическая энергия такой системы может возрастать 3) механическая энергия такой системы может убывать 4) механическая энергия такой системы может оставаться неизменной 5) векторная сумма всех внешних сил, действующих на эту систему равна нулю 6. Механическая система замкнута и консервативна. Верными являются утверждения: 1) векторная сумма всех внутренних сил, действующих в этой системе равна нулю 2) механическая энергия такой системы может возрастать 3) механическая энергия такой системы может убывать 4) механическая энергия такой системы остается неизменной 5) векторная сумма всех внешних сил, действующих на эту систему равна нулю 7. Тело массой m = 10 кг свободно падает с высоты Н =20 м с начальной скоростью V=0. Соотношение между кинетической Wкин и потенциальной энергией Wпот в точке на высоте h = 10 м от поверхности Земли 1) Wпот > Wкин 2) Wпот 20.На рисунке приведен график зависимости потенциальной энергии W n пружины от величины деформации х . Величина коэффициента упругости К пружины равна … 1) 210 5 Н/м 2) 410 5 Н/м 3) 1 10 5 Н/м 4) на основании рисунка коэффициент упругости пружины определить нельзя Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать  Движение по окружности с постоянной по модулю скоростьютеория по физике 🧲 кинематикаКриволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной. Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным. Особенности движения по окружности с постоянной по модулю скоростью:
Видео:Физика - движение по окружностиСкачать  Период, частота и количество оборотовПусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом. Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с). t — время, в течение которого тело совершило N оборотов За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости. Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц. N — количество оборотов, совершенных телом за время t. Период и частота — это обратные величины, определяемые формулами: Количество оборотов выражается следующей формулой: Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика. Видео:Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать  Линейная и угловая скоростиЛинейная скоростьЛинейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с. l — длина траектории, вдоль которой двигалось тело за время t Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна: R — радиус окружности, по которой движется тело Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство. Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим: Угловая скоростьУгловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с). ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан. За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период: Выражая угловую скорость через частоту, получим: Выразив частоту через количество оборотов, формула угловой скорости примет вид: Сравним две формулы: Преобразуем формулу линейной скорости и получим: Отсюда получаем взаимосвязь между линейной и угловой скоростями: Полезные факты
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых. В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах. За каждую секунду Земля проходит расстояние, равное примерно 30 км. Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать  Центростремительное ускорениеЦентростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время: Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли. Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд. Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу: Алгоритм решения
Решение Записываем исходные данные:
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела: Подставляем известные данные в формулу и вычисляем: pазбирался: Алиса Никитина | обсудить разбор | оценить Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним? а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза Алгоритм решения
Решение Запишем исходные данные: Центростремительное ускорение определяется формулой: Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно: Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений: Произведем сокращения и получим: Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б». pазбирался: Алиса Никитина | обсудить разбор | оценить Видео:Урок 90. Движение по окружности (ч.2)Скачать  Частица движется по окружности в соответствии с уравнением проекция угловой скорости через 2 сФ1.1.11-5
Ф1.1.11-6
Ф1.1.11-7
Ф1.1.11-8
Ф1.1.11-9
Ф1.1.12-1
Ф1.1.12-2
Ф1.1.12-3
Ф1.1.12-4
Ф1.1.12-5
Ф1.1.13-1
| ||||||||||||||||||||||||||||||||||||||||
 ,
, 

 ,
,  2)
2)  3)
3)  4)
4) 
 . Время движения до остановки равно … сек.
. Время движения до остановки равно … сек. . Проекция углового ускорения при этом движении равна
. Проекция углового ускорения при этом движении равна , где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна
, где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна
 2)
2) 
 4)
4) 



 и мгновенной скорости
и мгновенной скорости  с течением времени
с течением времени
 2)
2)  3)
3)  4)
4)  :1
:1
 , которые изображены на рисунке. Под действием этих сил точка начинает двигаться …
, которые изображены на рисунке. Под действием этих сил точка начинает двигаться …




 . При увеличении модуля силы и массы тела в два раза ускорение точки
. При увеличении модуля силы и массы тела в два раза ускорение точки





 2)
2)  3)
3)  4) ни одна из приведенных пар :2
4) ни одна из приведенных пар :2 2)
2)  , 4)
, 4) 
 2)
2)  3)
3)  4) определенного ответа дать нельзя :3
4) определенного ответа дать нельзя :3 ( масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар с средней силой
( масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар с средней силой  . Изменившийся импульс мяча стал равным
. Изменившийся импульс мяча стал равным . Импульс силы, действующий на мяч, направлен…
. Импульс силы, действующий на мяч, направлен…
 и
и  . Правильно показаны эти силы на рисунке номер …
. Правильно показаны эти силы на рисунке номер …


 2)
2)  3)
3)  4) ни в один из перечисленных моментов :2
4) ни в один из перечисленных моментов :2 . Модуль силы
. Модуль силы  одинаков во всех случаях. Работа силы будет минимальной и положительной в случае … :4
одинаков во всех случаях. Работа силы будет минимальной и положительной в случае … :4

 на всех графиках одинаковы, пройденные пути – так же. Одна и та же работа соответствует графикам
на всех графиках одинаковы, пройденные пути – так же. Одна и та же работа соответствует графикам 
 от расстояния, пройденного телом при равномерном прямолинейном движении. Сила изменяется по закону
от расстояния, пройденного телом при равномерном прямолинейном движении. Сила изменяется по закону  , где a=const . Работа силы
, где a=const . Работа силы 
 , где С – положительная константа. Знак мощности Р силы, действующей на точку, определяется неравенством …
, где С – положительная константа. Знак мощности Р силы, действующей на точку, определяется неравенством …

 .
. представлена выражением
представлена выражением 
 2)
2)  3)
3)  4)
4)  :2
:2
































 . Укажите направление вектора линейной скорости
. Укажите направление вектора линейной скорости  .
.
 ри равноускоренном движении направление угловой скорости
ри равноускоренном движении направление угловой скорости  совпадает с направлением углового ускорения
совпадает с направлением углового ускорения  или направление 2 в данном случае. Ответ: 1
или направление 2 в данном случае. Ответ: 1 
 , где φ – в радианах, t – в секундах. Число оборотов, совершенных частицей до остановки, равно…
, где φ – в радианах, t – в секундах. Число оборотов, совершенных частицей до остановки, равно… или
или  . Отсюда t1 = 3 c. Число оборотов, совершённых частицей за время t1, определяется соотношением
. Отсюда t1 = 3 c. Число оборотов, совершённых частицей за время t1, определяется соотношением  . Ответ: 3
. Ответ: 3  (R – радиус окружности, по которой движется частица). Величина
(R – радиус окружности, по которой движется частица). Величина  . После подстановки имеем
. После подстановки имеем  . Ответ: 1
. Ответ: 1  . Отсюда следует, что модуль тангенциального ускорения
. Отсюда следует, что модуль тангенциального ускорения  , где R – радиус окружности, по которой движется частица. Величина модуля углового ускорения
, где R – радиус окружности, по которой движется частица. Величина модуля углового ускорения  . Отсюда следует, что модуль углового ускорения есть величина постоянная и в момент времени t1 модуль тангенциального ускорения
. Отсюда следует, что модуль углового ускорения есть величина постоянная и в момент времени t1 модуль тангенциального ускорения  . Ответ: 1
. Ответ: 1  . Ответ: 1
. Ответ: 1  . Его угловое ускорение через 1 с от начала движения равно…
. Его угловое ускорение через 1 с от начала движения равно…

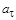 и нормальную
и нормальную 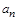 составляющие, причем
составляющие, причем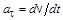 ,
, 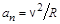 , (1.8)
, (1.8)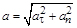 . (1.9)
. (1.9)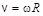 ;
; 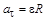 ;
; 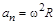 (1.10)
(1.10)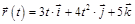 . Найдите тангенс угла между вектором скорости
. Найдите тангенс угла между вектором скорости 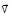 и осью х в момент времени
и осью х в момент времени 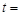 2 с.
2 с.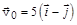 м/с, и с ускорением, которое зависит от времени по закону
м/с, и с ускорением, которое зависит от времени по закону 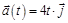 м/с 2 . Каков модуль скорости частицы в момент времени
м/с 2 . Каков модуль скорости частицы в момент времени 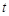 = 3 с.
= 3 с.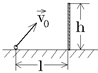 1.3. Маленькая лягушка находится на расстоянии l = 1 м от стенки и прыгает с начальной скоростью v 0 = 4 м/с. Стенку какой наибольшей высоты может перепрыгнуть лягушка? Принять g = 10 м/с 2 .
1.3. Маленькая лягушка находится на расстоянии l = 1 м от стенки и прыгает с начальной скоростью v 0 = 4 м/с. Стенку какой наибольшей высоты может перепрыгнуть лягушка? Принять g = 10 м/с 2 .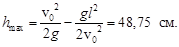
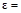 4 рад / c 2 . Через какой промежуток времени угол между вектором скорости и вектором ускорения точки на ободе колеса станет равным
4 рад / c 2 . Через какой промежуток времени угол между вектором скорости и вектором ускорения точки на ободе колеса станет равным 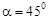 ?
?  Ответ:
Ответ: 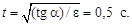
 к горизонту. Определить радиус кривизны его траектории сразу после прыжка, если в верхней точке траектория имеет радиус кривизны R = 40 см. Ответ:
к горизонту. Определить радиус кривизны его траектории сразу после прыжка, если в верхней точке траектория имеет радиус кривизны R = 40 см. Ответ: 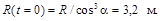
 1.6к. Радиус-вектор частицы изменяется во времени по закону
1.6к. Радиус-вектор частицы изменяется во времени по закону 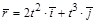 .
.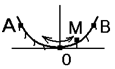 1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:
1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М: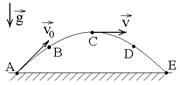 1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения
1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения 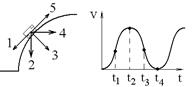 1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?
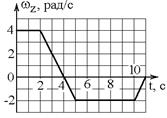
1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?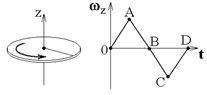 1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости
1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости 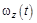 вектор угловой скорости
вектор угловой скорости 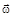 и вектор углового ускорения
и вектор углового ускорения 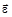 направлены в одну сторону? 1) 0 — А и А-В 2) 0 -А и В — С 3) В — С и С — D
направлены в одну сторону? 1) 0 — А и А-В 2) 0 -А и В — С 3) В — С и С — D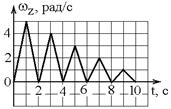 1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?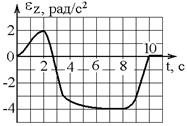 1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 = 7 с?
1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 = 7 с?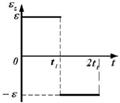 1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения
1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения 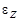 от времени представлена на графике. Соответствующая зависимость угловой скорости
от времени представлена на графике. Соответствующая зависимость угловой скорости 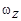 от времени представлена графиком .
от времени представлена графиком .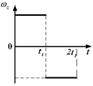 б)
б) 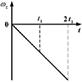 в)
в) 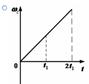 г)
г) 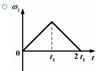
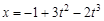 (в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна .
(в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна .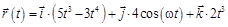 . Через сколько секунд перпендикулярной оси х окажется а) скорость частицы; б) ускорение частицы
. Через сколько секунд перпендикулярной оси х окажется а) скорость частицы; б) ускорение частицы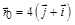 (м), со скоростью, которая зависит от времени по закону
(м), со скоростью, которая зависит от времени по закону 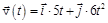 (м/с). На какое расстояние от начала координат удалится частица в момент времени
(м/с). На какое расстояние от начала координат удалится частица в момент времени 
 1.3с. Равнозамедленно вращающийся шкив повернулся на угол
1.3с. Равнозамедленно вращающийся шкив повернулся на угол 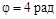 к тому моменту, когда его угловая скорость уменьшилась в три раза. Найти величину углового ускорения шкива. Его начальная скорость
к тому моменту, когда его угловая скорость уменьшилась в три раза. Найти величину углового ускорения шкива. Его начальная скорость 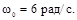
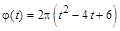 , где
, где 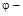 угол в радианах,
угол в радианах, 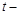 время в секундах. Величина нормального ускорения частицы равна нулю в момент времени (в секундах), равный: а) 1, б) 2, в) 3, г) 4
время в секундах. Величина нормального ускорения частицы равна нулю в момент времени (в секундах), равный: а) 1, б) 2, в) 3, г) 4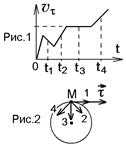 1.6с. Материальная точка M движется по окружности со скоростью
1.6с. Материальная точка M движется по окружности со скоростью 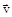 . На рис.1 показан график зависимости проекции скорости
. На рис.1 показан график зависимости проекции скорости 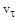 на орт
на орт 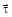 , направленный вдоль скорости
, направленный вдоль скорости