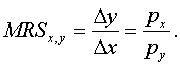Бюджетное ограничение и уравнение бюджетной линии оптимум равновесие потребителя (3 видео)

Бюджетное ограничение и оптимум потребителя

Содержание

Бюджетное ограничение и бюджетная линия
Бюджетная линия и оптимум потребителя
Равновесие потребителя
Оптимум потребителя
Бюджетное ограничение
📺 Видео

Видео:Оптимум для бюджетной прямойСкачать

Бюджетное ограничение и бюджетная линия

Потребитель располагает некоторым доходом (/), который он может истратить на два блага, цены которых даны. Тогда бюджетное ограничение потребителя:

где Хи Y— количества покупаемых благ, а — соответственно их цены.

Бюджетная линия отражает все комбинации двух благ, доступных потребителю при данном доходе и ценах (рис. 6.10).

Рис. 6.10. Бюджетная линия

В точке пересечения бюджетной линии с осью Y потребитель расходует весь свой доход на благо Y. При этом покупается единиц этого блага. В точке пересечения с осью X — все наоборот. Возможна и любая промежуточная комбинация.

Уравнение бюджетной линии выводится из бюджетного ограничения потребителя:

1. При росте (снижении) дохода потребителя бюджетная линия смещается вправо (влево) параллельно предыдущей (рис 6.11).

Рис. 6.11. Смещение бюджетной линии при изменении дохода

2. Наклон бюджетной линии равен соотношению цен В связи с этим, если товар Xдешевеет или товар Удорожает, наклон уменьшается. Если товар Xдорожает или товар Едешевеет, наклон увеличивается. Например, товар Xподешевел. Тогда наклон бюджетной линии уменьшается (рис. 6.12).

Рис. 6.12. Смещение бюджетной линии при падении цены блага X

Если по оси Y мы откладываем расходы на все остальные блага (М), то уравнение бюджетной линии принимает вид: М= I— Р_ххХ. Наклон бюджетной линии становится равен, следовательно, цене товара X.

В ряде случаев бюджетная линия может быть не стандартной. Например, фирма, производящая товар X, предлагает покупателю скидку на каждый следующий товар, покупаемый сверх определенного количества (А 1 *). В результате бюджетная линия становится ломаной (рис. 6.13).

Рис. 6.13. Ломаная бюджетная линия Оптимум потребителя

Соединим бюджетную линию и кривые безразличия на одном рисунке (рис. 6.14).

Рис. 6.14. Оптимум потребителя

Предположим, потребитель первоначально выбрал набор, соответствующий точке А. Такой набор не будет для него оптимальным, поскольку в данной точке наклон кривой безразличия превышает наклон бюджетной линии. Последнее означает, что предельная норма замены благом X блага Yздесь выше отношения их

цен: Таким образом, при увеличении потребления

блага X на 1 ед. потребителю придется уменьшить покупки блага Yна величину, равную отношению Но чтобы остаться на прежней кривой безразличия, потребитель мог бы отказаться от большего количества Y. В связи с этим, перераспределяя свои расходы в пользу блага X, потребитель реально переходит на более высокую кривую безразличия, т.е. увеличивает свое благосостояние.

Таким образом, максимум благосостояния потребителя будет достигнут в точке касания бюджетной линии и кривой безразличия (точка Е). Эта точка называется точкой потребительского оптимума, или точкой равновесия потребителя. Мы видим, что набор благ, соответствующий точке Е <X*,У*), относится к самой высокой из доступных потребителю кривых безразличия; все выше расположенные кривые просто не доступны при данном доходе и ценах.

Поскольку в точке потребительского оптимума наклон кривой безразличия равен наклону бюджетной линии, здесь соблюдается равенство

Если по оси Yоткладывать расходы на все прочие блага (М), то в точке оптимума предельная норма замены денег благом X равна цене данного блага

Видео:Бюджетное ограничениеСкачать

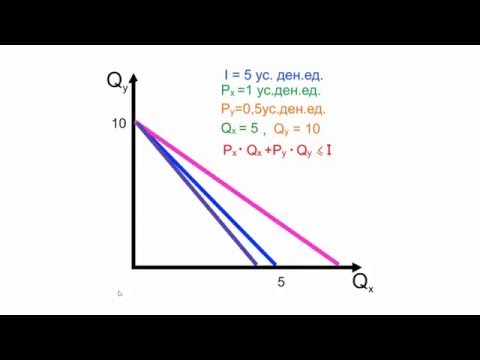
Бюджетная линия и оптимум потребителя

Карта безразличия представляет собой графическое отображение системы предпочтений потребителя. Естественно, потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Но он ограничен в своих средствах. Далеко не всякий товарный набор ему доступен. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия.

Обозначим месячный доход потребителя через I. Для упрощения предположим, что потребитель не делает никаких сбережений и весь свой доход расходует на приобретение только двух товаров X и Y. Бюджетное ограничение потребителя можно записать в форме следующего равенства:

Бюджетное ограничение имеет очевидный смысл: доход потребителя равен сумме его расходов на покупку товаров X и У. Преобразуем равенство (3.10) к следующему виду:

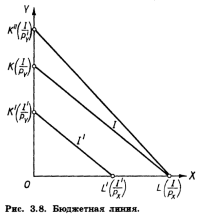
Мы получили уравнение бюджетной линии, или, как ее еще называют, линии цен. На рис. эта линия первоначально занимает положение KL.

Точки пересечения бюджетной линии с осями координат можно получить следующим образом. Если потребитель весь свой доход / израсходует только на покупку товара X, то он сможет приобрести I/PX единиц этого товара. Поэтому длина отрезка OL равна I/PX.

Аналогично можно показать, что длина отрезка ОК равна 1/РY. Наклон бюджетной линии равен -РX/РY — коэффициенту при X в уравнении (3.11).

Все товарные наборы, соответствующие точкам на бюджетной линии, стоят ровно / ман. и являются потому доступными для нашего потребителя. Все товарные наборы, расположенные выше и правее бюджетной линии, стоят более I ман. и недоступны для потребителя. Таким образом, бюджетная линия ограничивает сверху множество доступных для потребителя товарных наборов. Как изменится положение бюджетной линии при изменении дохода потребителя и цен на товары? Допустим сначала, что доход потребителя уменьшается до I

Наклон бюджетной линии не изменится, поскольку он определяется только соотношением цен. Следовательно, произойдет параллельный сдвиг бюджетной линии вниз. Она займет положение К’L’. При увеличении дохода и неизменных ценах будет наблюдаться параллельный сдвиг бюджетной линии вверх. Предположим теперь, что доход и цена товара X неизменны, цена же товара Y понизилась до РY

Оно показывает, что соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен на такую замену без изменения уровня полезности.

Изменение цены какого-либо товара влияет на объем спроса через эффект дохода и эффект замены. Это связано с тем, что в случае изменения цены происходят два процесса: во-первых, изменяется реальный доход индивида (при снижении цены товара доход относительно увеличивается); во-вторых, осуществляется относительная замена более дорогого товара более дешевым.

Можно определить, в какой мере изменение цены дает эффект дохода, а в какой – эффект замены. Это имеет существенное значение для фирм, продающих товары x и y, поскольку влияет на изменение кривых спроса на эти товары. Важно это и для правительства, осуществляющего компенсированное изменение дохода потребителя (индексацию) в соответствии с изменениями цен.

Видео:Как мыслит потребитель? Кривые безразличияСкачать

Равновесие потребителя

Принцип убывания предельной полезности лежит в основе анализа соотношения количества и качества благ, на которые потребитель предъявляет спрос, т.е. осуществляет свой потребительский выбор. Потребляя одновременно много благ, каждый индивид приобретает для себя такой их набор, в котором предельные полезности каждого блага равны или приносят ему одинаковое удовлетворение.

Цель потребителя – получение максимальной полезности от приобретенного им на рынке набора благ. Максимизация полезности достигается тогда, когда отношение предельной полезности блага к его цене станет одинаковым у всех благ из набора, который приобретается покупателем:

где MU1, MU2 и MUi – предельная полезность 1-го, 2-го и i-го блага; Р1, Р2 и Pi – цена 1-го, 2-го и i-го блага.

Это равенство принято называть равновесием потребителя (2-й закон Госсена).

Равновесие потребителя – это равенство отношений предельных полезностей различных благ к их ценам.

Видео:ИнЭИ Экономика Лекция №1.1 «Теория потребительского поведения»Скачать

Оптимум потребителя

Ситуация с пресной водой, рассмотренная ранее, не является типичным примером потребительского выбора, поскольку в ней не хватает таких элементов, как альтернативы (выбор из двух или большего количества благ) и ограничения (ограниченный бюджет).

Вернемся к примеру с водой. Только теперь добавим альтернативу воде (пусть это будут пирожки) и введем ограничения (бюджет 100 руб.). Цена 1 пирожка составляет 20 руб., а стакана воды – 10 руб. Как в такой ситуации будет вести себя потребитель? Как уже было отмечено, рациональный потребитель всегда стремится к максимизации полезности. Следовательно, он может весь бюджет потратить только на пирожки, и тогда он купит 5 пирожков. Возможна ситуация, что весь бюджет потребитель потратит на воду – 10 стаканов. Как бы сильно ни нравились данному индивиду пирожки, он не получит от пятого пирожка того же удовлетворения, что от первого. Гораздо вероятнее, что он откажется от пятого пирожка и вместо него купит два стакана воды. В этом случае индивид увеличит полученную общую полезность, так как первые стаканы воды принесут большое удовлетворение, в то время как пятый пирожок – очень незначительное. По мере того как будет сокращаться потребление пирожков, а потребление воды увеличиваться, предельная полезность пирожков будет возрастать, а воды – уменьшаться.

В некоторый момент времени индивид окажется в ситуации, когда он не сможет дальше увеличивать общую полезность, расходуя большую сумму на одно благо и меньшую на другое в рамках ограниченного бюджета – он достигнет точки потребительского оптимума.

Оптимум потребителя – это максимизация полезности от потребления набора блат в рамках офаниченного бюджета.

Проиллюстрируем это на примере. Нам понадобятся кривая безразличия (изокванта) и бюджетная линия (изокоста).

Кривая безразличия. Предельная норма замещения

Кривая безразличия – это кривая, показывающая все возможные комбинации наборов благ, обладающих равной полезностью.

Первым понятие «кривая безразличия» ввел в научный оборот Ф. Эджуорт. Эта кривая наглядно отражает все возможные наборы альтернативных благ X и Y, одновременное потребление которых приносит потребителю одинаковое удовлетворение (рис. 3.2, а).

Исследуя потребительские предпочтения более полно, можно построить карту безразличия (рис. 3.2, б), т.е. множество кривых безразличия, которые характеризуются равными полезностями на одной линии и разными – на разных линиях U1, U2, U3. Кривые безразличия, отстоящие дальше от начала координат, характеризуют наборы с бо́льшей полезностью. Карта безразличия дает полную информацию о системе предпочтений потребителя, не требуя абсолютного количественного измерения полезности.

Рис. 3.2. Кривая (а) и карта (б) безразличия

Свойства кривых безразличия:

• абсолютная величина наклона кривой безразличия в любой точке называется предельной нормой замещения MRS (Marginal rate of substitution) блага X благом У. Она может быть вычислена по формуле

В нашем примере

Предельная норма замещения – это отношение предельной полезности по товару X к предельной полезности по товару Y.

• кривые безразличия являются вогнутыми (т.е. выпуклыми к началу координат). Это обусловлено принципом убывающей предельной полезности, согласно которому чем большим количеством одного блага располагает потребитель, тем все меньшим количеством другого блага он готов жертвовать при обмене;
• кривые безразличия не могут пересекаться. В случае, если имеет место пересечение, нарушаются все три аксиомы: полной упорядоченности, транзитивности и ненасыщенности;
• наклон кривых безразличия может меняться в зависимости от индивидуальных предпочтений потребителя.

Рис. 3.3. Карта безразличия фотомодели (а) и рабочего (б)

На рис. 3.3, а представлена карта безразличия для потребителя, который большее удовлетворение получает от потребления воды (фотомодель), а на рис. 3.3, б – карта потребителя, который большее удовлетворение получает от потребления пирожков (рабочий).

Видео:Курсы по экономике ВШЭ Микроэкономика 3.1 Поведение потребителяСкачать

Бюджетное ограничение

На индивидуальный выбор влияет покупательная способность потребителя, которая определяется, с одной стороны, бюджетом потребителя, с другой – уровнем цен на приобретаемые им товары.

I – располагаемый доход покупателя – 100 руб.;

X – количество пирожков, которое можно приобрести;

Y – количество воды, которое можно приобрести;

РХ – цена пирожка;

РY – цена стакана воды.

ΡX • X – сумма денежных средств, затраченная на пирожки;

ΡY • Y – сумма денежных средств, затраченная на воду.

Бюджетное ограничение – это верхняя граница множества рыночных возможностей потребителя или бюджетная линия.

В этом случае покупательная способность может быть выражена уравнением

I = (РХ • X) + (РY • Y).

Это уравнение принято называть уравнением бюджетной линии. Из него следует: Ι/ΡX, Ι/ΡY – максимальное количество собственно пирожков и воды, которое может приобрести покупатель.

Величину Υ можно найти, используя уравнение бюджетной линии

где РX/РY – угловой коэффициент бюджетной линии.

Продолжим рассмотрение нашего примера и составим таблицу, в которой представим все возможные комбинации распределения бюджета потребителя (100 руб.) на приобретение пирожков и воды (табл. 3.2).

Таблица 3.2

Распределение бюджета потребителя