Блок схема решения системы линейных уравнений методом зейделя (3 видео)

Интерполяционный метод Гаусса-Зейделя

Этот метод исключительно удобен для использования на ЭВМ.

Рассмотрим систему из трех уравнений с тремя неизвестными:

Предположим, что а_иФ 0; а_и Ф 0; а₃₃ Ф 0, и перепишем систему в следующем виде:

Теперь возьмем некоторое первое приближение к решению этой системы, обозначив его через х, (0) , х₂ х* 01 . Подставим это решение в (3.18) и вычислим новое значение х, (1) :

Используя только что вычисленное значение х<'* и начальное значение * 0) = 0, х ( 2 >] = 0, х = 0, как это обычно делается для начального приближения. Тогда, согласно формулам:

Получаем следующее приближение:

Последовательные приближения, вычисленные каждый раз с точностью до четырех значащих цифр, приведены в табл. 3.1.

Для системы из п уравнений с п неизвестными (диагональные элементы отличны от нуля) к-е приближение к решению будет задаваться функцией

Интерполяционный процесс продолжается до тех пор, пока все х- к) не станут достаточно близки к х^

г> . Критерий близости можно задавать в следующем виде:

где определяется максимальное значение разности для всех /, a s — некоторое положительное число.

Достаточным условием сходимости метода Гаусса-Зейделя является то, что диагональные члены должны преобладать в уравнении, т. е. они должны быть по абсолютной величине не меньше, а по крайней мере в одном случае больше недиагональных элементов для всех или для одного /:

Блок-схема алгоритма решения системы линейных уравнений итерационным методом Гаусса-Зейделя представлена на рис. 3.2, программа расчета на языке Паскаль приведена в приложении.

В качестве практического примера использования методов решения систем линейных уравнений приведем поиск коэффициентов параболической аппроксимации по набору экспериментальных точек (см. пример 5.8 раздела 5.3.3). Решение этого примера надежнее проводить с помощью прямого метода Гаусса, т. к. условие сходимости итерационного метода Гаусса-Зейделя может не выполниться. Блок-схема алгоритма расчета представлена на рис. 3.3. Программа расчета на языке Паскаль приведена в приложении. Матрица коэффициентов системы линейных уравнений обозначена двумерным массивом аа, искомые коэффициенты параболической аппроксимации — массивом а.

Содержание

Вопросы для самоконтроля
1.2.3. Метод Зейделя (метод Гаусса-Зейделя, метод последовательных замещений)
Итерационные методы решения системы линейных алгебраических уравнений
Общие сведения об итерационных методах или методе простой итерации
Метод Якоби
Метод Зейделя
Метод простой итерации
💥 Видео

Видео:Метод Зейделя Пример РешенияСкачать

Вопросы для самоконтроля

1. В чем состоит постановка задачи при решении систем линейных уравнений?
2. Какие знаете методы решения линейных уравнений?
3. На чем основано решение систем линейных уравнений методом Гаусса?
4. Сущность метода Гаусса-Зейделя?

Рис. 3.2. Блок-схема решения системы линейных уравнений методом Гаусса-Зейделя

Рис. 3.3. Блок-схема расчета коэффициентов квадратичной аппроксимации зависимости теплоемкости циклопропана от температуры с использованием метода Гаусса

Видео:6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

1.2.3. Метод Зейделя (метод Гаусса-Зейделя, метод последовательных замещений)

Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения неизвестных x1, х2, .

В этом методе, как и в методе простой итерации, необходимо привести систему к виду (3), чтобы диагональные коэффициенты были максимальными по модулю, и проверить условия сходимости. Если условия сходимости не выполняются, то нужно произвести элементарные преобразования (см. п. 4). Пусть дана система из трех линейных уравнений. Приведем ее к виду (3). Выберем произвольно начальные приближения корней: х1(0), х2(0), х3(0), стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным. За нулевое приближение можно принять столбец свободных членов, т. е. х(0) = b

(т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3). Найдем Первое приближение х(1) по формулам:

Следует обратить внимание на особенность метода Зейделя, которая состоит в том, что полученное в первом уравнении значение х1(l) сразу же используется во втором уравнении, а значения х1(1), х2(1) – в третьем уравнении и т. д. То есть все найденные значения х1(1) подставляются в уравнения для нахождения хi+1(1) [6, 8].

Рабочие формулы для метода Зейделя для системы трех уравнений имеют следующий вид:

Запишем в общем виде для системы n-уравнений рабочие формулы:

Заметим, что теорема сходимости для метода простой итерации справедлива и для метода Зейделя.

Зададим определенную точность решения e, по достижении которой итерационный процесс завершается, т. е. решение продолжается до тех пор, пока не будет выполнено условие для всех уравнений: где i=1,2,3,…,n.

Пример №2. Методом Зейделя решить систему с точностью e = 10-3:

1. Приведем систему к виду:

2. В качестве начального вектора х(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:

3. Проведем итерации методом Зейделя. При k = 1

При вычислении х2(1) используем уже полученное значение х1(1) =

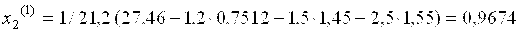
При вычислении х3(1) используем значения х1(1) и х2(1):

Наконец, используя значения х1(1), х2(1), х3(1), получаем:

Аналогичным образом ведем вычисления при k=2 и k=3. При k= 2:

Найдем модули разностей значений при k = 2:

Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,80006, x2 = 1,00002, x3 = 1,19999, x4 = 1,40000.

Видео:Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Видео:9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Видео:Метод простой итерации Пример РешенияСкачать

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .