Блок схема по системе уравнений

В этой статье будут рассмотрены примеры блок-схем, которые могут встретиться вам в учебниках по информатике и другой литературе. Блок-схема представляет собой алгоритм, по которому решается какая-либо задача, поставленная перед разработчиком. Сначала нужно ответить на вопрос, что такое алгоритм, как он представляется графически, а самое главное – как его решить, зная определенные параметры. Нужно сразу отметить, что алгоритмы бывают нескольких видов.

Видео:3 Метод простой итерации Блок-схема Решение системы линейных уравнений СЛАУСкачать

Что такое алгоритм?

Это слово ввел в обиход математик Мухаммед аль-Хорезми, который жил в период 763-850 года. Именно он является человеком, который создал правила выполнения арифметических действий (а их всего четыре). А вот ГОСТ от 1974 года, который гласит, что:

Алгоритм – это точное предписание, которое определяет вычислительный процесс. Причем имеется несколько переменных с заданными значениями, которые приводят расчеты к искомому результату.

Алгоритм позволяет четко указать исполнителю выполнять строгую последовательность действий, чтобы решить поставленную задачу и получить результат. Разработка алгоритма – это разбивание одной большой задачи на некую последовательность шагов. Причем разработчик алгоритма обязан знать все особенности и правила его составления.

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Особенности алгоритма

Всего можно выделить восемь особенностей алгоритма (независимо от его вида):

1. Присутствует функция ввода изначальных данных.
2. Есть вывод некоего результата после завершения алгоритма. Нужно помнить, что алгоритм нужен для того, чтобы достичь определенной цели, а именно – получить результат, который имеет прямое отношение к исходным данным.
3. У алгоритма должна быть структура дискретного типа. Он должен представляться последовательными шагами. Причем каждый следующий шаг может начаться только после завершения предыдущего.
4. Алгоритм должен быть однозначным. Каждый шаг четко определяется и не допускает произвольной трактовки.
5. Алгоритм должен быть конечным – необходимо, чтобы он выполнялся за строго определенное количество шагов.
6. Алгоритм должен быть корректным – задавать исключительно верное решение поставленной задачи.
7. Общность (или массовость) – он должен работать с различными исходными данными.
8. Время, которое дается на решение алгоритма, должно быть минимальным. Это определяет эффективность решения поставленной задачи.

А теперь, зная, какие существуют блок-схемы алгоритмов, можно приступить к рассмотрению способов их записи. А их не очень много.

Видео:0.Блок схема. 8 классСкачать

Словесная запись

Такая форма, как правило, применяется при описании порядка действий для человека: «Пойди туда, не знаю куда. Принеси то, не знаю что».

Конечно, это шуточная форма, но суть понятна. В качестве примера можно привести еще, например, привычную запись на стеклах автобусов: «При аварии выдернуть шнур, выдавить стекло».

Здесь четко ставится условие, при котором нужно выполнить два действия в строгой последовательности. Но это самые простые алгоритмы, существуют и более сложные. Иногда используются формулы, спецобозначения, но при обязательном условии – исполнитель должен все понимать.

Допускается изменять порядок действий, если необходимо вернуться, например, к предыдущей операции либо обойти какую-то команду при определенном условии. При этом команды желательно нумеровать и обязательно указывается команда, к которой происходит переход: «Закончив все манипуляции, повторяете пункты с 3 по 5».

Видео:Решение системы уравнений методом ГауссаСкачать

Запись в графической форме

В этой записи участвуют элементы блок-схем. Все элементы стандартизированы, у каждой команды имеется определенная графическая запись. А конкретная команда должна записываться внутри каждого из блоков обычным языком или математическими формулами. Все блоки должны соединяться линиями – они показывают, какой именно порядок у выполняемых команд. Собственно, этот тип алгоритма более подходит для использования в программном коде, нежели словесный.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Запись на языках программирования

В том случае, если алгоритм необходим для того, чтобы задачу решала программа, установленная на ПК, то нужно его записывать специальным кодом. Для этого существует множество языков программирования. И алгоритм в этом случае называется программой.

Видео:Блок схема.Работа в ворде. WordСкачать

Блок-схемы

Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости).

Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.

Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Основные правила составления блок-схемы

Можно выделить такие особенности, которые должны быть у любой блок-схемы:

1. Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
2. От начального блока до конечного должны быть проведены линии связи.
3. Из всех блоков, кроме конечного, должны выходить линии потока.
4. Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо. Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
5. Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия. Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
6. Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
7. От начального блока в схеме линия потока только выходит, так как он является самым первым.
8. А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
9. Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
10. Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
11. Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.

Графические элементы блок-схем для решения алгоритмов представлены в таблице:

Видео:Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

Линейный тип алгоритмов

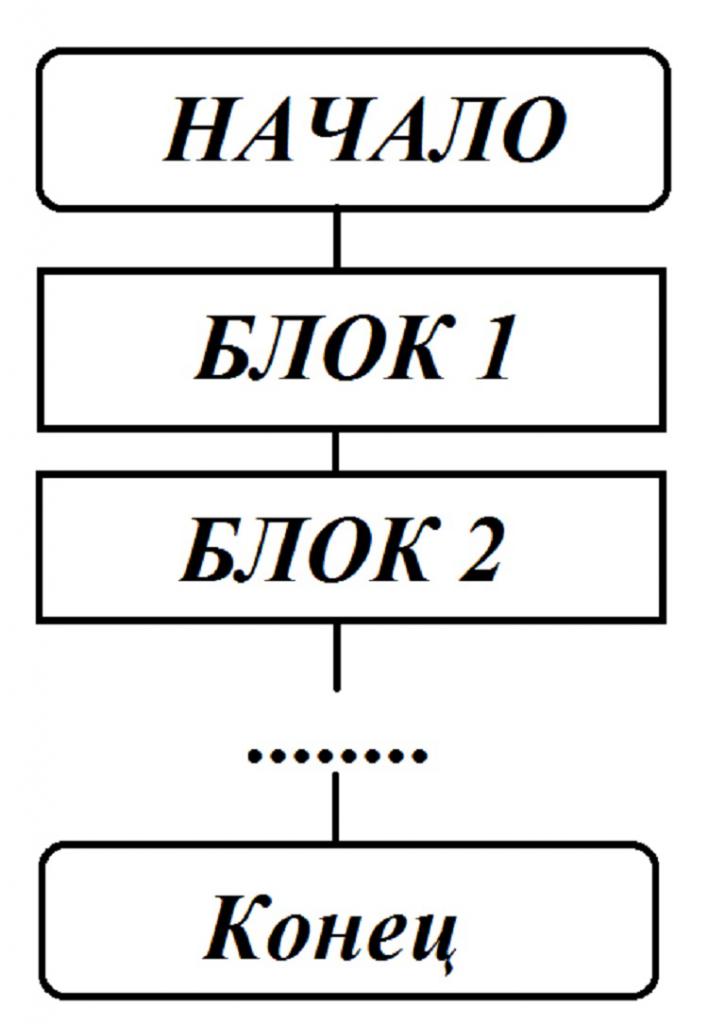
Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:

Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.

Видео:Решаем задачи в виде блок-схемы (7 класс)Скачать

Разветвляющиеся алгоритмы

Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.

На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы:

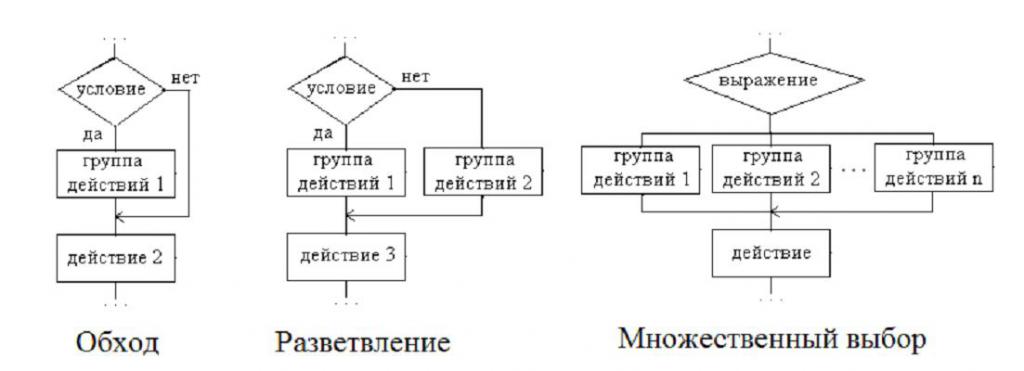
1. «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки.
2. «Разветвление» – каждая ветка имеет определенный набор выполняемых действий.
3. «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм.

Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.

Видео:Как быстро нарисовать блок-схемы бизнес-процессов для технического задания CRMСкачать

Циклический алгоритм

Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов:

1. У которых известно число повторений действий (их еще называют циклами со счетчиком).
2. У которых число повторений неизвестно – с постусловием и предусловием.

Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.

Видео:Решение систем уравнений методом подстановкиСкачать

Циклы со счетчиками

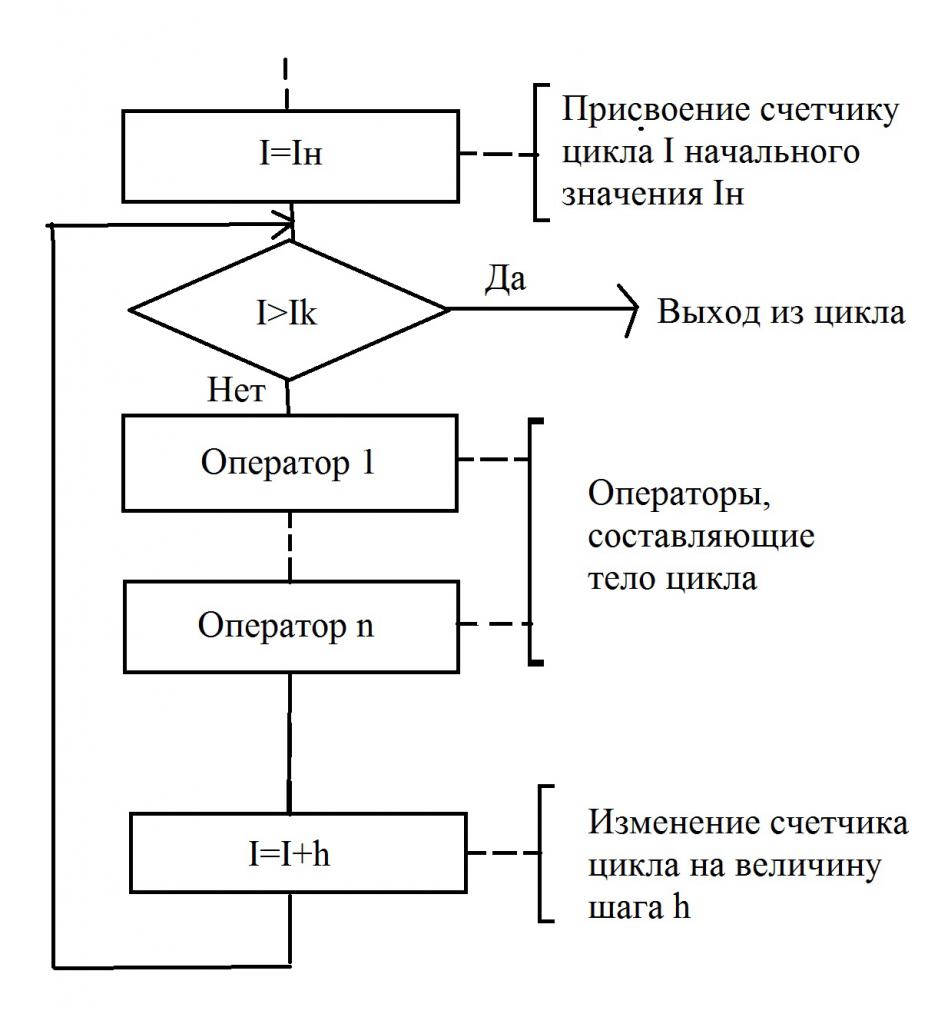
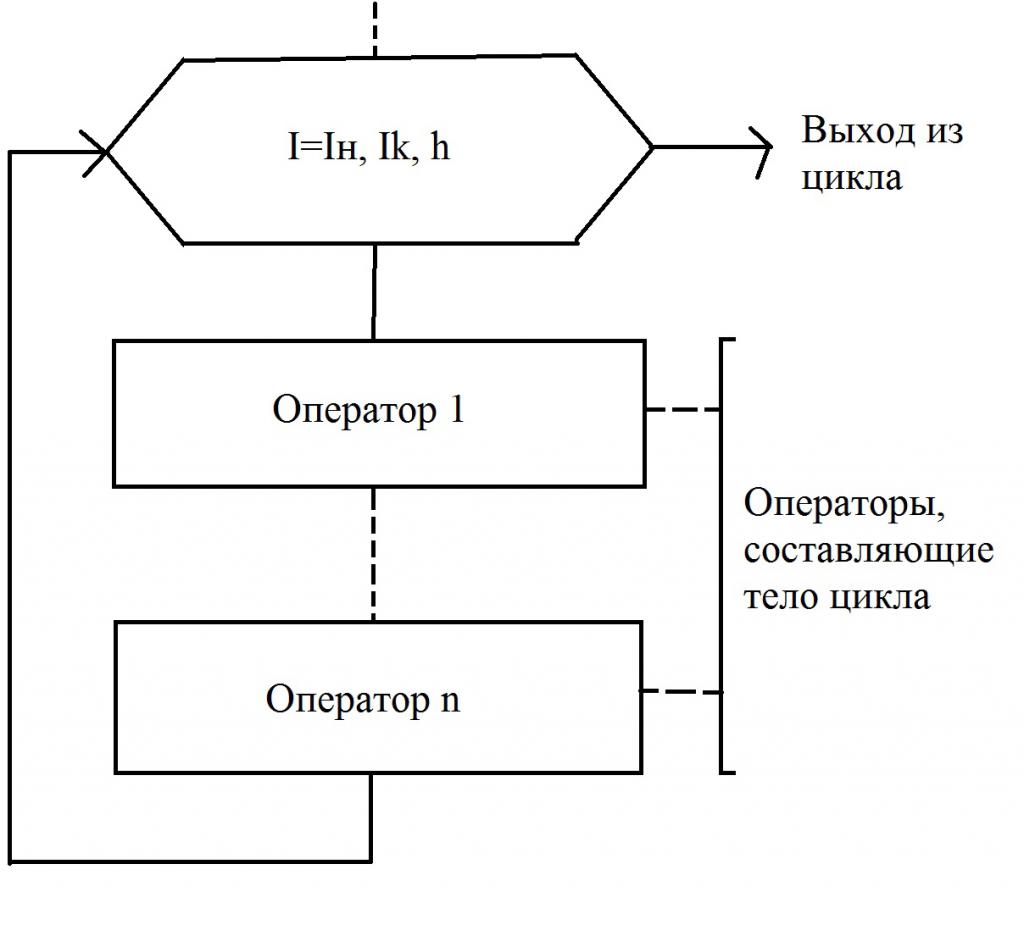
На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.

Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла.

После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.

Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору.

Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия:

1. В теле не разрешается изменять (принудительно) значение счетчика.
2. Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.

Видео:Математика это не ИсламСкачать

Циклы с предусловием

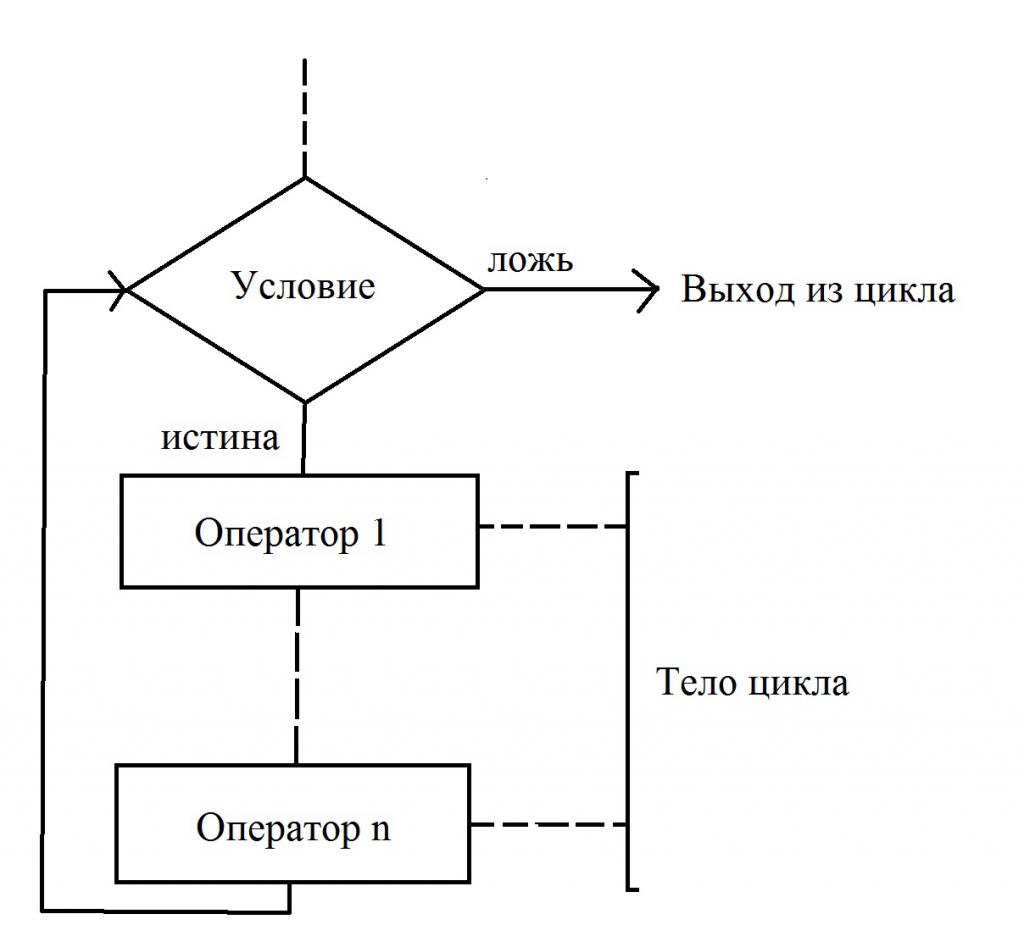
Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы.

В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход.

В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма).

Ниже приведена блок-схема, которая описывает все эти действия:

Видео:Построение блок-схемы расчета значения арифметического выраженияСкачать

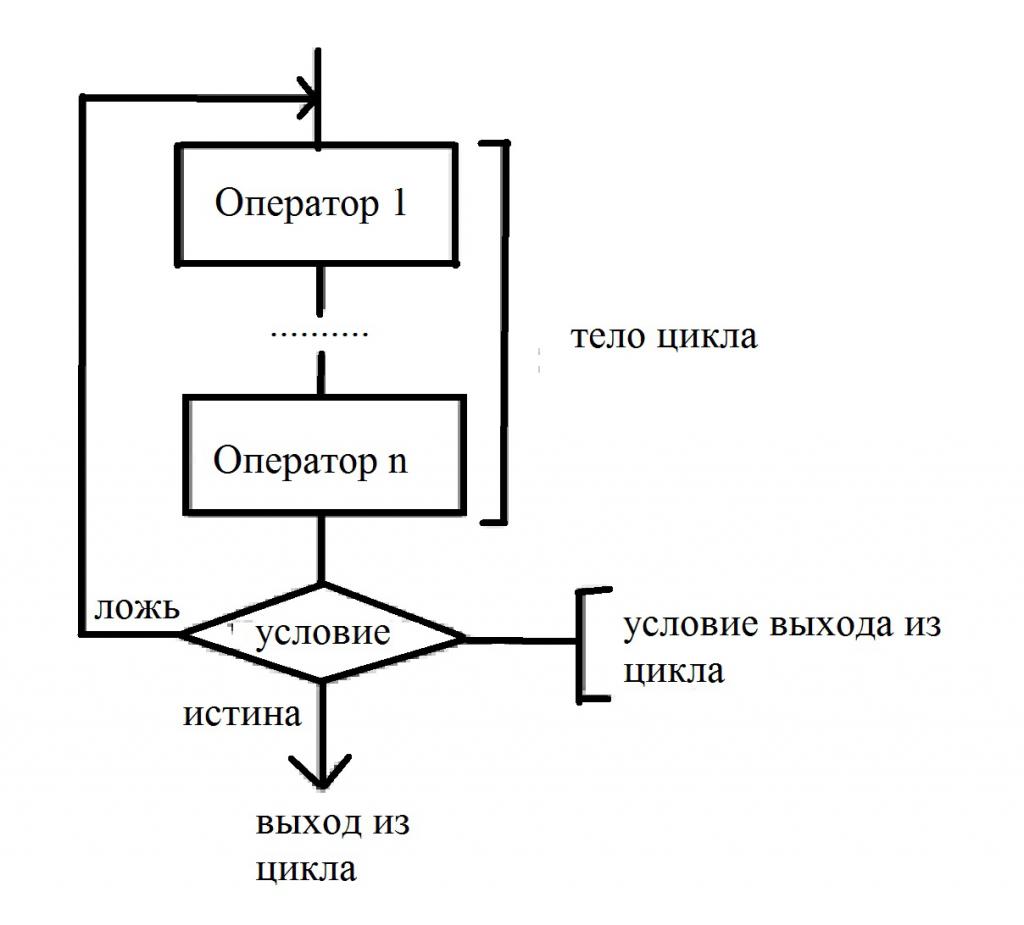
Что такое цикл с постусловием?

Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:

Ничего сложного в построении алгоритмов с циклами нет, достаточно в них только один раз разобраться. А теперь перейдем к более сложным конструкциям.

Видео:Основы программирования / Урок #6 – Блок схемы и алгоритмы действийСкачать

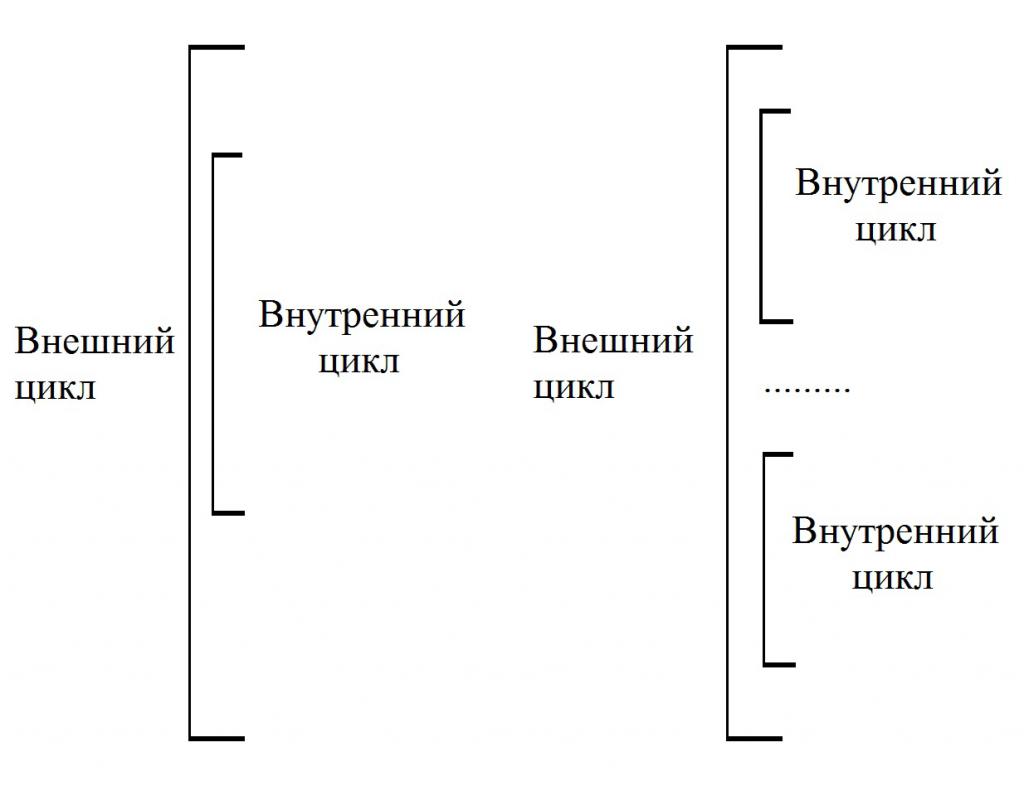
Сложные циклы

Сложные – это такие конструкции, внутри которых есть один или больше простых циклов. Иногда их называют вложенными. При этом те конструкции, которые охватывают иные циклы, называют «внешними». А те, которые входят в конструкцию внешних – внутренними. При выполнении каждого шага внешнего цикла происходит полная прокрутка внутреннего, как представлено на рисунке:

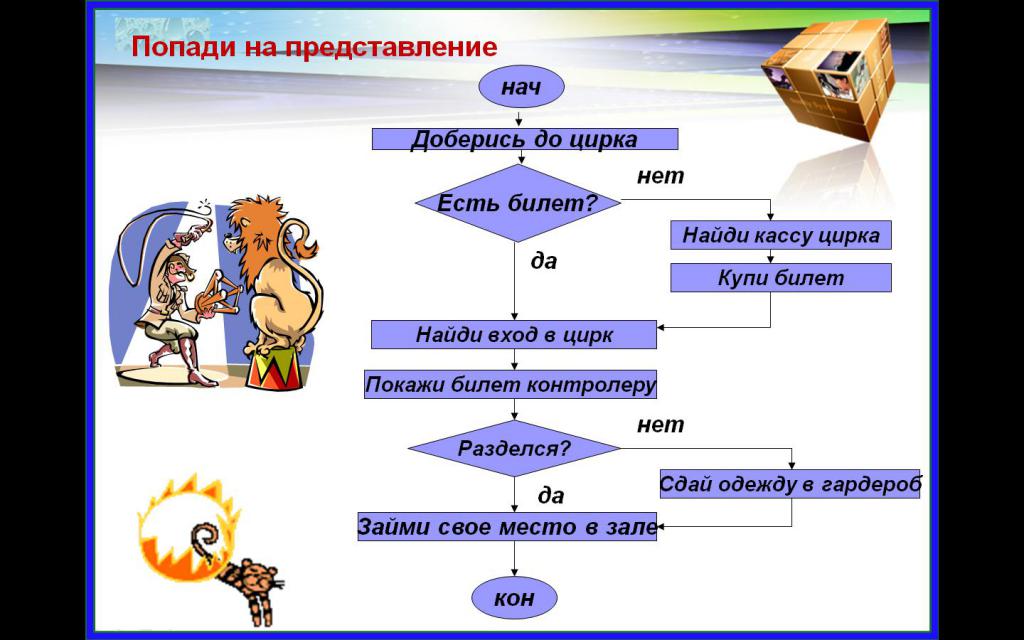
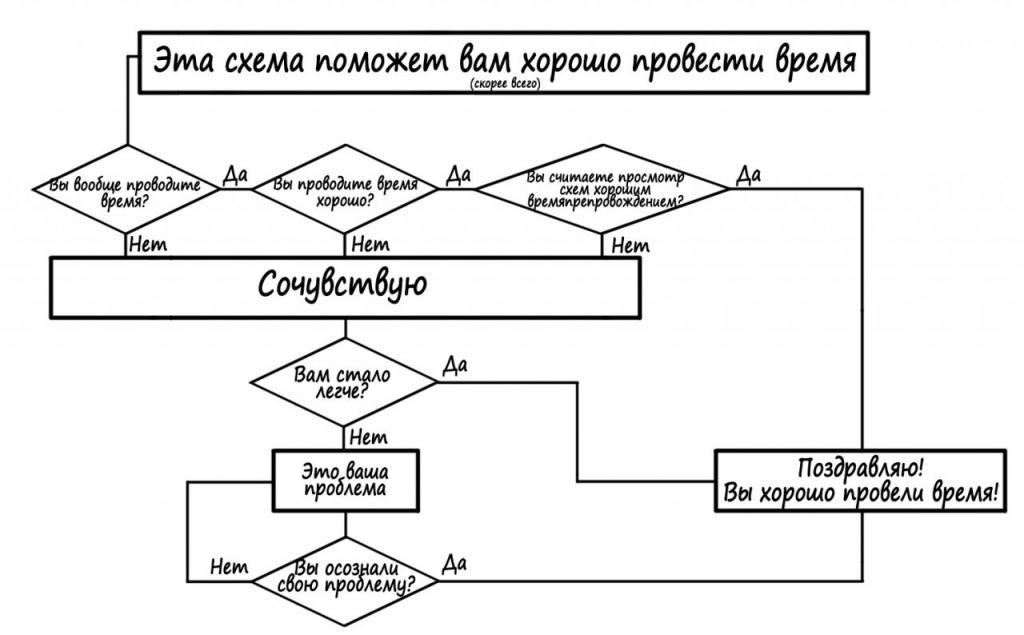
Вот и все, вы рассмотрели основные особенности построения блок-схем для решения алгоритмов, знаете принципы и правила. Теперь можно рассмотреть конкретные примеры блок-схем из жизни. Например, в психологии такие конструкции используются для того, чтобы человек решил какой-то вопрос:

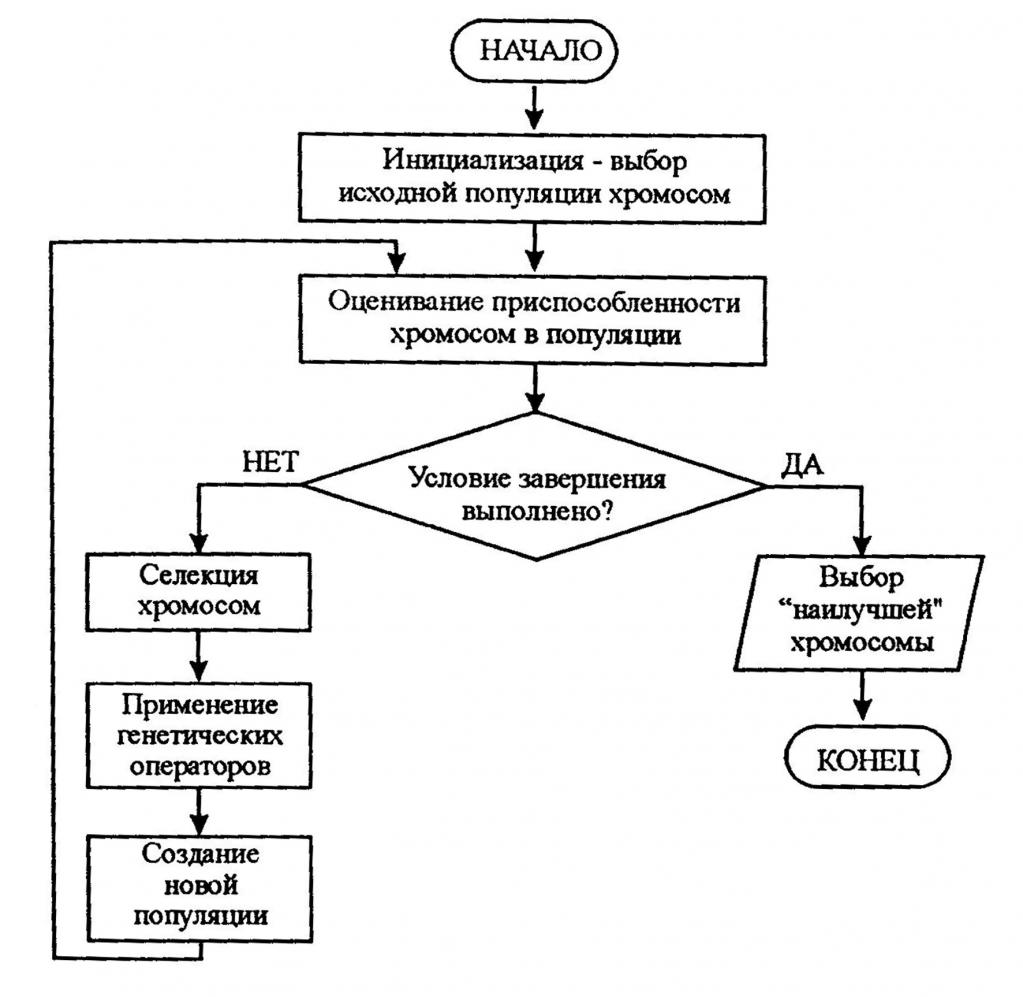
Или пример из биологии для решения поставленной задачи:

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Решение задач с блок-схемами

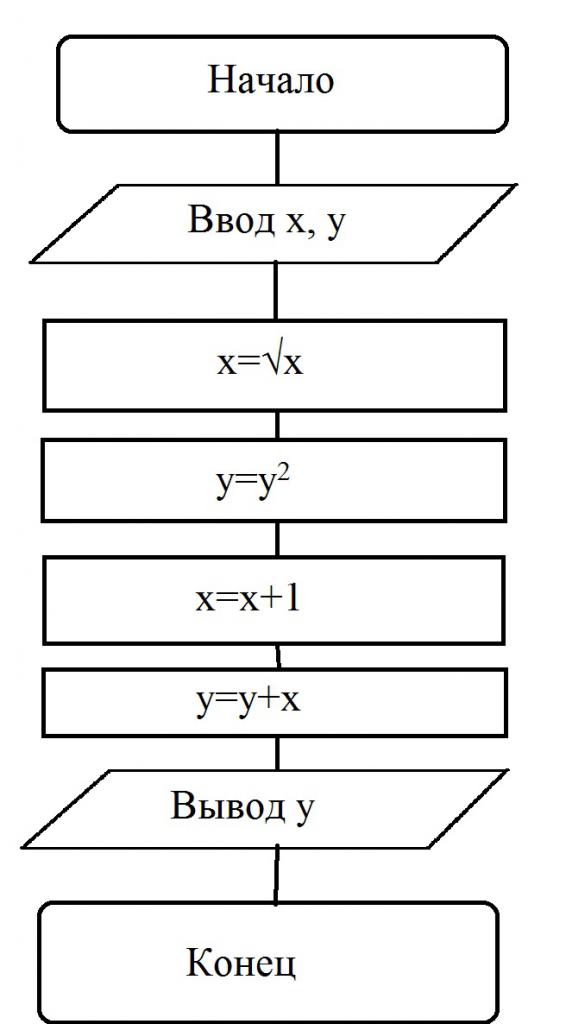
А теперь рассмотрим примеры задач с блок-схемами, которые могут попасться в учебниках информатики. Например, задана блок-схема, по которой решается какой-то алгоритм:

При этом пользователь самостоятельно вводит значения переменных. Допустим, х=16, а у=2. Процесс выполнения такой:

1. Производится ввод значений х и у.
2. Выполняется операция преобразования: х=√16=4.
3. Выполняется условие: у=у 2 =4.
4. Производится вычисление: х=(х+1)=(4+1)=5.
5. Дальше вычисляется следующая переменная: у=(у+х)=(5+4)=9.
6. Выводится решение: у=9.

На этом примере блок-схемы по информатике хорошо видно, как происходит решение алгоритма. Нужно обратить внимание на то, что значения х и у задаются на начальном этапе и они могут быть любыми.

Видео:6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

Программирование системы уравнений

1 Постановка задачи

2 Решение системы уравнения методом Гаусса

3 Решение уравнения методами Ньютона, Хорд

4 Разработка блок схемы решения системы уравнения методом Гаусса

5 Разработка блок схемы решения уравнения методом Ньютона

6 Разработка блок схемы решения уравнения методом Хорд

7 Язык программирования Turbo Pascal

8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal

9 Разработка программы решения уравнения методом Ньютона при помощи Turbo Pascal

10 Разработка программы решения уравнения методом Хорд при помощи Turbo Pascal

Список используемых источников

В основе того или иного языка программирования лежит некоторая руководящая идея, оказывающая существенное влияние на стиль соответствующих программ.

Исторически первой была идея структурирования программ, в соответствии с которой программист должен был решить, какие именно процедуры он будет использовать в своей программе, а затем выбрать наилучшие алгоритмы для реализации этих процедур. Появление этой идеи было следствием недостаточной изученности алгоритмической стороны вычислительных процессов, столь характерной для ранних программных разработок (сороковые — пятидесятые годы). Типичным примером процедурно-ориентированного языка является Фортран – первый и всё ещё один из наиболее популярных языков программирования. Последовательное использование идеи процедурного структурирования программ привело к созданию обширных библиотек программирования, содержащих множество сравнительно небольших процедур, из которых, как из кирпичиков, можно строить «здание» программы.

По мере прогресса в области вычислительной математики акцент в программировании стал смещаться с процедур в сторону организации данных. Оказалось, что эффективная разработка сложных программ нуждается в действенных способах контроля правильности использования данных. Контроль должен осуществляться как на стадии компиляции, так и при прогоне программ, в противном случае, как показала практика, резко возрастают трудности создания крупных программных проектов. Отчётливое осознание этой проблемы привело к созданию Ангола-60, а позже Паскаля, Модулы-2, Си и множества других языков программирования, имеющих более или менее развитые структуры типов данных. Логическим следствием развития этого направления стал модульный подход к разработке программ, характеризующийся стремлением «спрятать» данные и процедуры внутри модуля.

Начиная с языка Симула-67, в программировании наметился новый подход, который получил название объектно-ориентированного программирования (в дальнейшем ООП). Его руководящая идея заключается в стремлении связать данные с обрабатывающими эти данные процедурами в единое целое – объект. Характерной чертой объектов является инкапсуляция (объединение) данных и алгоритмов их обработки, в результате чего и данные, и процедуры во многом теряют самостоятельное значение.

1 Постановка задачи

Цель решения задачи курсовой работы – автоматизация решения системы уравнения методом Гаусса, а так же решения уравнения методами Хорд и Ньютона.

Выходная информация задачи выводиться на экран монитора.

Входная информация задачи поступает путем ввода пользователем данных для решения поставленной задачи

Прекращение решения задачи выполняется при выходе нового программного обеспечения, связанного с решением данной задачи или появление новой версии данного продукта.

2 Решение системы уравнения методом Гаусса

Метод Гаусса— классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных.

Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах», составленном между I в. до н.э. и II в. н. э.

Видео:Решение систем уравнений методом сложенияСкачать

Описание метода

Пусть исходная система выглядит следующим образом

Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к ступенчатому виду:

Переменные называются главными переменными. Все остальные называются свободными.

Если , то рассматриваемая система несовместна.

Предположим, что .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ( , где — номер строки):

,

где

Если свободным переменным системы (2) придавать все возможные значения и вычислить через них главные переменные, то мы получим все решения. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях полученное нами решение является решением системы (1).

1: Если в совместной системе все переменные главные, то такая система является определённой.

2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.

Условие совместности.

Упомянутое выше условие может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

1) На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получавшуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

2) На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

В простейшем случае алгоритм выглядит так:

3) Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:

1) нахождения матрицы, обратной к данной (к матрице справа приписывается единичная такого же размера, что и исходная: , после чего приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица: );

2) определения ранга матрицы (согласно следствию из теоремы Кронекера—Капелли ранг матрицы равен числу её главных переменных);

3) численного решения СЛАУ в вычислительной технике (ввиду погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Система т линейных уравнений с п неизвестными имеет вид:

b_i — свободные члены (или правые части)

Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.

Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными , если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1) перемена местами двух любых уравнений;

2) умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

( 1 )

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁ . Получим уравнение:

( 2 )

где

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а ₂₁ и а ₃₁ ).

Система примет вид:

( 3 )

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂ из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

( 4 )

где

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

В результате преобразований система приняла вид:

(5)

Система вида (5) называется треугольной.

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х₃ подставляют во второе уравнение системы (5) и находят х₂ . Затем х₂ и х₃ подставляют в первое уравнение и находят х₁ .

В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.

Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b¹ 0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.

Ступенчатая система имеет вид:

Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х_{k +1} , … , x_k переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х₁ , … , x_k , которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.

Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.

3 Решение уравнения методами Ньютона, Хорд

Метод хорд (способ пропорциональных частей) — численный метод уточнения корня трансцендентного уравнения.

Точный корень уравнения находится на отрезке . Производная на этом промежутке непрерывна и сохраняет постоянный знак. Приближенный корень , при котором , можно найти используя метод хорд. Для этого нужно взять начальное приближение корня и применить к нему итерационную формулу:

линейный уравнение хорда гаусс ньютон

, , если

, , если

, ,

В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала (рисунок 1).

Здесь вычисляются значения функции на концах отрезка и строится “хорда”, соединяющая точки (a, f(a)) и (b, f(b)). Точка пересечения ее с осью абсцисс

принимается за очередное приближение к корню. Анализируя знак f(z) в сопоставлении со знаком f(x) на концах отрезка, сужаем интервал до [a,z] или [z,b] и продолжаем процесс построения хорд до тех пор, пока разница между очередными приближениями не окажется достаточно малой (в пределах допустимой погрешности) |Z_n -Z_n-1 | * — корень уравнения, Z_n и Z_n+1 — очередные приближения, m и M – наименьшее.

Пусть корень уравнения отделен на отрезке [a, b], причем и непрерывны и сохраняют определенные знаки при . Если на некотором произвольном шаге n найдено приближенное значение корня , то можно уточнить это значение по методу Ньютона. Положим

(1)

где считаем малой величиной. Применяя формулу Тейлора, получим:

Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня

Геометрически метод Ньютона эквивалентен замене дуги кривой касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что при и (см. рис.).

Выберем, например, , для которого . Проведем касательную к кривой в точке B₀ с координатами .

В качестве первого приближения корня возьмем абсциссу точки пересечения касательной с осью Ox. Через точку снова проведем касательную, абсцисса точки пересечения которой даст второе приближение корня и т.д.

Формулу для уточнения корня можно получить из прямоугольного треугольника , образованного касательной, проведенной в точке , осью абсцисс и перпендикуляром, восстановленным из точки .

Имеем

Так как угол образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е.

Тогда

или для любого шага n

.

В качестве начальной точки можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие

т.е. функция и ее вторая производная в точке должны быть одного знака.

В качестве простейших условий окончания процедуры уточнения корня рекомендуется выполнение условия

Как следует из последнего неравенства, требуется при расчете запоминать три значения аргумента . В практических инженерных расчетах часто применяют сравнение аргументов на текущей и предыдущей итерациях:

При составлении программы решения уравнения методом Ньютона следует организовать многократный расчет приближений для корня. Если удается получить аналитическое выражение для производной, то ее вычисление, а также вычисление можно оформить в виде функций.

4 Разработка блок схемы решения системы уравнения методом Гаусса

5 Разработка блок схемы решения уравнения методом Ньютона

6 Разработка блок схемы решения уравнения методом Хорд

7 Язык программирования Turbo Pascal

Turbo Pascal является реализацией Pascal’я. Самая первая версия Pascal быля разработана на кафедре информатики Стэндфордского университета швейцарским ученым Николаусом Виртом в 1968 году.

С момента появления Pascal на рынке продуктов прошло много времени прежде чем он получил всеобщее признание. В середине 80-х годов американской фирмой Borland International, Inc была создана реализация языка Pascal, известная и по сей день под именем Turbo Pascal. Эта фирма объединила очень быстрый компилятор с редактором текста и добавила к стандартному Паскалю мощное расширение, что способствовало успеху первой версии этого языка.

В 1985 году на рынке ПЭВМ появился язык программирования Турбо Паскаль (версия 3.0) с компилятором стандартного Паскаля. С тех пор Паскаль стал применяться в общеобразовательных, профессионально-технических школах и в сфере высшего образования в качестве «первого» языка программирования. Благодаря простоте использования язык Турбо Паскаль получил широкое распространение и в любительских кругах. Повышению популярности Турбо Паскаля способствовал набор небольших сопутствующих программ (Toos), позволяющих получать чрезвычайно компактную, быструю и легко читаемую программу. Эти качества Турбо Паскаля были высоко оценены и в среде профессиональных программистов. Встроенный редактор текста использует достаточно широко распространенную систему команд, берущую начало от пакета WordStar и хорошо знакомую каждому, кто интенсивно использует ПЭВМ.

В появившемся со временем пакете Турбо Паскаль 4.0 было устранено большинство подвергавшихся критике ограничений компилятора и была повышена производительность системы. Кроме того, новый компилятор версии 4.0 имел существенные отличия от предыдущей версии. Наиболее важным нововведением была ИNIТ-концепция, заимствованная из языка Модула-2. Это дало возможность реализовать в рамках ТП разработку крупных программных продуктов.

С выходом в свет версии 5.0 ТП получил еще большие шансы на благосклонную реакцию со стороны профессиональных пользователей благодаря встроенному в среду программирования интегрированному отладчику, который позволил повысить производительность труда.

Существенно улучшила технические характеристики ТП реализация аппарата перекрытий (overlays), позволяющего строить мощные программные комплексы, рассчитанные на эксплуатацию в малых по объему областях памяти. Суть механизма перекрытий сводится к делению программы на части, поочередно загружаемые по мере необходимости с дискеты или жесткого диска в одну и ту же область памяти, заменяя при этом находившуюся там часть программы.

Кроме того, в ТП 5.0 были расширены возможности отладки программ и обеспечена возможность поддержки расширенной памяти в стандарте Lotus-Intel-Microsoft (SLIMS/EMS 4.0). Сокращение EMS обозначает Expanded Memory Specification (спецификация расширенной памяти). Нельзя путать этот вид дополнительной памяти с другим — Extended Memory. EMS имеется на обычных ПЭВМ класса XT, в то время как Extended Memory — только на машинах АТ-класса (с процессором 286, 386 и выше) при объеме памяти свыше 1 Мбайта.

В этой версии были также исправлены и улучшены библиотеки графических процедур, поставляемые вместе с пакетом ТП и обеспечивающие полную совместимость с графическими адаптерами класса VGA (Video Graphics Array).

В рамках версии ТП 5.5 были осуществлены дальнейшие преобразования в направлении улучшения технических характеристик пакета. Наряду с внутренними улучшениями и новыми возможностями встроенной справочной системы Help, а также большим набором учебных примеров, важным нововведением явилась реализация в языке концепции объектно-ориентированного программирования (ООП).

Через некоторое время на рынке появился ТП 6.0, в котором теоретическая концепция объектно-ориентированного программирования была реализована практически с полным набором объектов, которые могли использоваться для решения прикладных задач. Кроме того, реализация системы меню приведена в соответствие со стандартом SAA (Turbo Vision). В качестве практического примера использования новых возможностей был реализован текстовый редактор, встроенный в IDE

Integrated Development Environment — интегрированную инструментальную оболочку. При этом сторонники программирования на ТП 6.0 получили возможность не только работать со встроенным многооконным текстовым редактором, но и использовать мышь, которая значительно облегчает работу пользователя.

В 1992 году фирма Borland International представила пользователям очередную версию языка Паскаль — Турбо Паскаль 7.0. Наряду со всеми преимуществами, которые унаследованы от предыдущей версии (многооконный режим работы, возможность использования мыши, возможность использования языка программирования низкого уровня Ассемблер, возможность создавать объектно-ориентированные программы), в ТП 7.0 были произведены изменения и улучшения. Во-первых: появилась возможность выделять определенным цветом различные элементы исходного текста (зарезервированные слова, идентификаторы, числа и т. д.), позволяющая даже неопытным пользователям устранять ошибки на этапе ввода исходного текста. Во-вторых: язык программирования ТП 7.0 был расширен (появилась возможность использовать типизированный адресный оператор, открытые массивы и строки и т. д.), что предоставило пользователю дополнительные возможности при решении повседневных задач. В-третьих: был улучшен компилятор, вследствие чего «коды программ» стали более эффективными. В-четвертых: был улучшен интерфейс пользователя. Кроме того, в ТП 7.0 расширены возможности объектно-ориентированного программирования (в частности, расширены и улучшены возможности Turbo Vision).

8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal

A:array[1..N,1..N] of real = ((9.1, 5.6, 7.8),

Видео:5 Метод половинного деления Блок-схема Численные методы решения нелинейного уравненияСкачать

Основные блок-схемы решения линейных и квадратичных задач с параметрами

Разделы: Математика

Задачи с параметрами (ЗсП) традиционно являются наиболее сложными для учащихся, поскольку требуют от них умения логически рассуждать и проводить анализ решения. Подобные задачи являются первыми исследовательскими задачами, с которыми встречаются школьники. Для их решения не требуются знания, выходящие за пределы школьной программы, но недостаточно применения лишь стандартных приемов, а необходимо глубокое понимание всех разделов элементарной математики.

В данной статье предпринята попытка систематизации и формализации (в форме блок-схем) наиболее часто встречающихся и наиболее типичных ЗсП. При этом выделены классы задач, решаемых по единой методике.

Рассматриваются аналитические методы решения ЗсП, сводящиеся к исследованию линейных или квадратных уравнений (неравенств), а также квадратного трехчлена. Такой выбор обусловлен тем, что курс школьной математики ограничен «вглубь», по существу, «теорией квадратичного».

Линейные уравнения

Определение. Уравнение вида ax=b, где a, b принадлежат множеству всех действительных чисел, будем называть стандартным видом линейного уравнения. Всевозможные варианты, возникающие при решении линейных уравнений, отразим в блок–схеме I.

Количество корней линейного уравнения отразим в блок-схеме II:

Пример 1. Для всех действительных значений параметра m решите уравнение m 2 x–2=4x+m.

Решение. Приведем заданное линейное уравнение к стандартному виду:

m 2 x–2=4x+m, m 2 x–4x=m+2, (m 2 –4)x=m+2.(1)

Следуя схеме I, рассмотрим два случая для коэффициента при x:

1)если m 2 – 4 не равно 0, m не равно ±2, то x=(m+2)/(m 2 -4), x=1/(m–2);

а) при m = –2 уравнение (1) примет вид 0х=0, отсюда х – любое действительное число;

б) при m = 2 уравнение (1) примет вид 0х= 4, отсюда следует, что корней нет.

Ответ. Если m 2 то x=1/(m–2); если m= – 2, то x – любое действительное число; если m=2, то корней нет.

Пример 2. При каких значениях параметра k уравнение 2(k–2x)=kx+3 не имеет корней?

Решение. 2(k–2x)=kx+3, (k+4)x=2k–3. В силу схемы II уравнение не имеет корней, если k+4=0 и 2k–3 не равно 0 => k= –4 и k не равно 1,5 => k = –4.

Ответ. k=–4.

Системы линейных уравнений

Определение 1. Система называется совместной, если она имеет хотя бы одно решение.

Определение 2. Система называется несовместной, если она не имеет ни одного решения.

Количество решений системы линейных уравнений отразим в блок-схеме III.

Замечание. Так как уравнение прямой y=kx+b в общем виде записывается следующим образом ax+by+c=0, то взаимное расположение двух прямых отразим в блок-схеме IV.

Пример. При каких значениях параметра c система из двух уравнений c 2 x+(2–c)y–4=c3 и (2c–1)y+cx+2=c 5 совместна?

Решение. Запишем систему в стандартном виде: c 2 x+(2–c)y=c 3 +4 и cx+(2c–1)y=c 5 –2. Сначала найдем значения c, при которых эта система не имеет решений. В силу схемы III имеем условие,

c 2 /с=(2-с)/(2с–1), с не равно (c 3 +4)/(c 5 –2),

которое равносильно системе из уравнения и неравенства

с=(2–с)/(2с–1) и с не равно (c 3 +4)/(c 5 –2).

Решением системы является с=1. Итак, система имеет решения при всех действительных значениях с, кроме с=1.

Ответ. с — любое действительное число, с не равно 1.

Линейные неравенства

Определение. Неравенство вида ax>b, ax b, ax b, отразим в блок-схеме V.

Пример. Для всех значений параметра m решите неравенство 5x–m>mx–3.

Решение. 5x–m>mx–3, (5–m)x>m–3.

Следуя схеме V, рассмотрим три случая для коэффициента при х:

2)если 5–m 5, то x 2. Откуда следует, что решений нет.

Ответ. Если m (m–3)/(5–m); если m=5, то решений нет; если m>5, то х 2 +bx+c=0, где a, b, c — любые действительные числа, a>0, называется квадратным уравнением относительно действительного переменного x.

Ситуации, возникающие при решении квадратных уравнений, отразим в блок–схеме VI.

Пример. При каких значениях параметра c уравнение (c–2)x 2 +2(с–2)x+2=0 не имеет корней?

Решение. Рассмотрим два случая:

1) если с–2 не равно 0, c не равно 2, то D 2 –2(c–2) 2 +(c+4)x+c+7=0 имеет только отрицательные корни?

Решение. В силу условия задачи необходимо рассмотреть два случая (линейный и квадратичный):

1) если c–1=0, c=1, то уравнение примет вид 5x+8=0, x= –5/8 – отрицательный корень;

2) если c–1 не равно 0, c не равно 1, то, следуя схеме VII, получим систему

Решением ее являются промежутки –22/3 2 +bx+c, где a не равно 0, называется квадратичной. График квадратичной функции называется параболой.

Абсциссы точек пересечения параболы y=ax 2 +bx+c с осью (Ox) являются корнями уравнения ax 2 +bx+c=0.

Учитывая это, отразим взаимное расположение параболы и оси (Ox) в следующей схеме:

Замечание. Если уравнение параболы имеет вид y=a(x–p) 2 +q, то (p; q) – координаты вершины параболы.

Пример 1. При каких значениях параметра a вершина параболы y=(x–7a) 2 +a 2 –10+3a лежит в III координатной четверти?

Решение. Пусть (x₀, y₀) – координаты вершины параболы. В силу замечания имеем x₀=7a, y₀=a 2 –10+3a. Так как вершина параболы лежит в третьей четверти, то

Ответ. –5

Пример 2. При каких значениях параметра b график функции y=(4–b 2 )x 2 +2(b+2)x–1 лежит ниже оси (Ox)?

Решение. Рассмотрим два случая.

1. Пусть 4–b 2 =0, b= + 2;

1) если b=2, то прямая y=8x–1 не лежит ниже оси (Ox);

2) если b= –2, то прямая y= –1 лежит ниже оси (Ox).

2. Пусть 4–b 2 не равно 0. Тогда в соответствии со схемой VIII получим

Объединяя ответы, получим b 2 +bx+c=0. Введем функцию y(x)= ax 2 +bx+c. Тогда расположение корней этого уравнения на числовой оси отразим в блок–схеме IX.

Следствие. С учетом схемы IX схема VII для знаков корней квадратного уравнения примет следующий вид:

Пример. При каких значениях параметра a корни уравнения x 2 –2(a+3)x+a 2 +6,25a+8=0 больше 2?

Решение. Введем функцию y(x)=x 2 –2(a+3)x+a 2 +6,25a+8; x₀ – абсцисса вершины этой параболы. Так как корни уравнения находятся справа от числа 2, то в соответствии со схемой IX имеем:

Решение. Данная задача равносильна следующей: при каких значениях параметра b система

имеет одно решение?

Решим неравенство (2): 2x 2 –2x–1>0, x_1,2=0,5(1±(3) 1/2 ), x 1/2 ) или x>0,5(1+(3) 1/2 ).

Найдем корни уравнения (1): D=(2b–7) 2 , x₁=2, x₂=2b–5. Поскольку корень x₁=2 удовлетворяет неравенству (2), то система имеет одно решение в следующих случаях:

1) если x₂=2b–5 не удовлетворяет неравенству (2), то 0,5(1–(3) 1/2 ) 1/2 ) или 0,25(11–O3) 1/2 );

Ответ. 0,25(11–(3) 1/2 ) 1/2 ), b=3,5.

Пример 2. При каких значениях параметра p уравнение 5–4sin 2 x–8cos 2 (x/2)=3p имеет корни?

Решение. Преобразуем заданное уравнение:

5– 4sin 2 x–8cos 2 (x/2)=3p => 5–4(1–cos2x)–4(1+cosx)=3p => 4cos 2 x–4cosx–3p–3=0.

Сделаем замену cosx=t. Тогда заданная задача равносильна следующей: при каких значениях p система

4t2–4t–3p–3=0, (1)
-1 2 –4t–3p–3; t₀–вершина этой параболы. В силу схемы IX случаи 1, 2 и 3 описываются следующей совокупностью:

📸 Видео

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать