Блок схема алгоритма решения дифференциальных уравнений методом эйлера (6 видео)

дифференциальных уравнений

Ряд задач, возникающих перед инженерами-механиками при проектировании или исследованиях металлургических машин, сводится к решению обыкновенных дифференциальных уравнений. С помощью таких уравнений описываются модели динамики объектов, как правило, они отражают изменение параметров объектов во времени.

В общем случае обыкновенное дифференциальное уравнение имеет вид:

или y¢ = f(x,y) . (65)

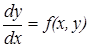
Решением дифференциального уравнения является функция y= y(x), отыскание которой выполняется интегрированием дифференциального уравнения. При использовании численных методов решение уравнения (65) представляется в табличном виде, т.е. получается совокупность значений y_i и x_i.

Одним из основных типов задач для обыкновенных дифференциальных уравнений является задача Коши, которая для дифференциального уравнения первого порядка заключается в нахождении решения уравнения:

удовлетворяющего при x=x₀ начальному условию

Интегрируя (66) в пределах от x до x+h (где h – шаг), получим:

. (68)

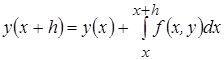
В зависимости от вида функции, аппроксимирующей подынтегральную функцию (константа; прямая, проходящая через концы отрезка; парабола и т.д.) получают различные формулы численного интегрирования дифференциального уравнения.

Решение дифференциального уравнения численными методами носит шаговый характер, т.е. по одной или по нескольким начальным точкам (x, y) за один шаг находят следующую точку, затем следующую и т.д. Разница между двумя соседними значениями аргумента x называется шагом: h = x_i+1 — x_i.

Выделяют два класса методов решения: одношаговые и многошаговые. Первый класс методов требует для нахождения следующего значения функции y= y(x) только одной текущей точки, а второй – нескольких. Поэтому методами второго класса нельзя начать решение задачи Коши, это всегда делается одношаговыми методами.

Основная идея получения простейших вычислительных алгоритмов в одношаговых методах сводится к следующему. Зная значение y в точке разложения y_i и производную f(x_i , y_i), находят значение функции y(х) через шаг h:

Основными одношаговыми методами решения дифференциальных уравнений являются методы Эйлера и Рунге-Кутта [6, 7]. Рассмотрим их вычислительные алгоритмы.

Использование любого из методов начинается с выбора фиксированного шага h по переменной х:

, (70)

где x_к – конечная точка интервала интегрирования;

n — количество шагов интегрирования.

Далее используется одна из приближенных формул вычисления функции y=y(x) в точке x₀+h. Принимая эту точку в качестве начальной, определяют y(x₀+2h). Этот прием повторяют необходимое количество раз и вычисляют значения y(x) в конечной точке. При необходимости сохраняют массив значений y(x₀+ih), что дает возможность построить график y=y(x).

Наиболее простым методом решения дифференциальных уравнений первого порядка (66) является метод Эйлера.

Для определения значений функции y=y(x) используется выражение:

Для начала вычислений используются начальные условия (67).

На рисунке 35 приведена графическая интерпретация метода Эйлера. В точке (x_i , y_i) функция y=y(x) аппроксимируется отрезком, проходящим через нее под углом a_i. Угол a_i определяется значением производной в точке (x_i , y_i), т.е. tg a_i = f(x_i , y_i).

Блок схема алгоритма решения дифференциальных уравнений методом эйлера

Рисунок 35 – Графическая интерпретация метода Эйлера

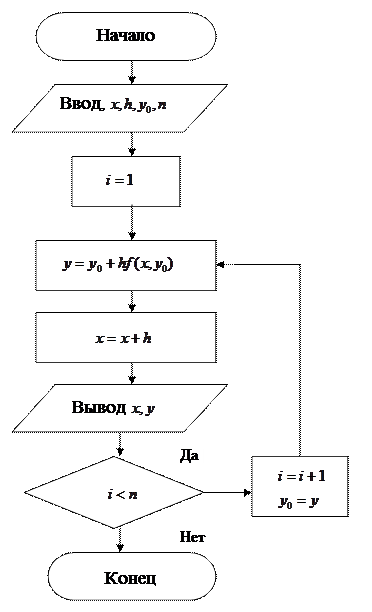
Блок-схема алгоритма решения представлена на рисунке 36.

Рисунок 36 – Блок-схема алгоритма решения дифференциального уравнения методом Эйлера

Метод Эйлера обладает большой погрешностью и имеет систематическое накопление ошибок (см. рисунок 35). Погрешность метода пропорциональна h 2 .

Для повышения точности на практике используют модифицированный метод Эйлера. Он имеет следующий вычислительный алгоритм:

На рисунке 37 изображено графическое пояснение формулы (72). Здесь через точку (x_i , y_i) проводится прямая L₁ под углом a_i ( tg a_i = f(x_i , y_i) ) и определяется точка А с координатами (x_i+0.5h, y_i+0.5h f(x_i, y_i)). В точке А вычисляется производная, которая определяет угол наклона прямой L₂ , т.е. tg b_i = f(x_i+0.5h, y_i + 0.5h f(x_i, y_i)). Через точку (x_i , y_i) параллельно L₂ проводится прямая L до пересечения с вертикальной прямой, исходящей из точки на оси х с абсциссой x_i+1 . Отсекаемый при этом отрезок на вертикальной прямой и определяет значение функции y=y(x) равное y_i+1 при x=x_i+1, соответствующее вычисленному по (72).

Рисунок 37 – Графическое пояснение вычислений по модифицированному методу Эйлера

Блок-схема алгоритма решения дифференциального уравнения модифицированным методом Эйлера приведена на рисунке 38. Этот метод дает погрешность пропорциональную h 3 .

Наиболее распространенным методом решения задачи Коши (66)-(67) является метод Рунге-Кутта четвертого порядка. Этот метод более точен по сравнению с методами Эйлера. Для расчета одного значения функции необходимо четыре раза вычислить правую часть дифференциального уравнения (66), а не два, как в модифицированном методе Эйлера.

Рисунок 38 – Блок-схема алгоритма решения дифференциального уравнения модифицированным методом Эйлера

Вычислительный алгоритм метода основывается на следующих выражениях:

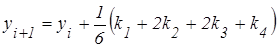
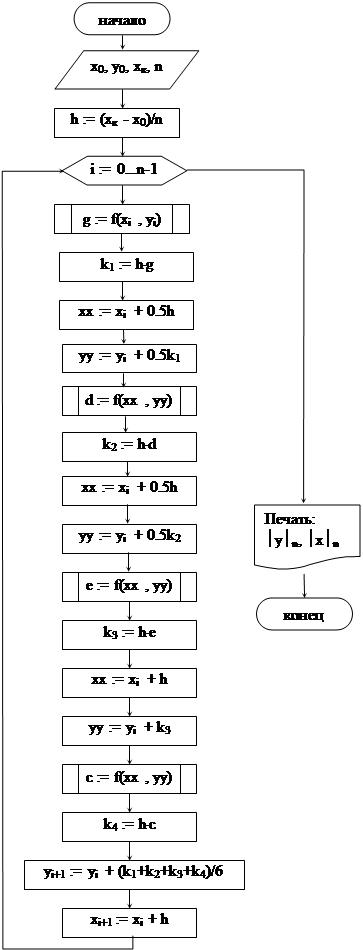
Блок-схема алгоритма решения дифференциального уравнения методом Рунге-Кутта четвертого порядка приведена на рисунке 39.

Погрешность метода Рунге-Кутта пропорциональна h 5 .

Рисунок 39 – Блок-схема алгоритма решения дифференциального уравнения методом Рунге-Кутта четвертого порядка

СПИСОК ЛИТЕРАТУРЫ

1. Тимошенко Г.М., Зима П.Ф. Теория инженерного эксперимента. – К.: УМК ВО, 1991. – 124 с.

2. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высш. шк., 1990. – 544 с.

3. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. – М.: Наука, 1987. – 240 с.

4. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: Раско, 1991. – 272 с.

5. TURBO PASCAL: Алгорітми і програми: Чисельні методи в фізиці та математиці. – К.: Вища шк., 1992. – 247 с.

6. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика, 1999. – 256 с.

7. Гловацкая А.П. Методы и алгоритмы вычислительной математики. – М.: Радио и связь, 1999. – 408 с.

8. Пироженко Н.Г. Расчет параметров привода металлургических машин. – Донецк: ДонГТУ: кафедра МОЗЧМ. – 1999. – 84 с.

9. Левин М.З., Седуш В.Я. Механическое оборудование доменных цехов. – Киев-Донецк: Вища школа, 1978. – 1978. – 176 с.

10. Механическое оборудование сталеплавильных цехов / Левин М.З., Седуш В.Я., Мачикин В.И. и др. – Киев-Донецк: Вища школа, 1985. – 165 с.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Блок-схема метода Эйлера.

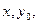
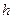
Задаются начальные значения величина шага и количество

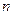
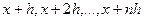
расчетных точек , как показано на рисунке 17.1. Решение получается в узлах . Вывод результатов предусмотрен на каждом шаге.

Рисунок 17.1 Блок-схема метода Эйлера.

Понятие решения краевой задачи.

Если при решении обыкновенных дифференциальных уравнений

задаются условия для двух значений независимой переменной (на концах рассматриваемого отрезка), то такие задачи называются краевыми.

Рассмотрим линейное дифференциальное уравнение второго порядка:

. (17.1)

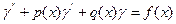
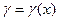
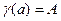
Краевая задача состоит в отыскании решения уравнения (17.1) на отрезке [а,b], удовлетворяющего на концах отрезка условиям

; . (17.2)

Граничные условия могут быть заданы не только в частном виде (17.2), но и в общем:

. (17.3)

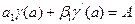
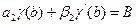
Методы решения краевых задач могут быть:

точные аналитические, приближенные и численные.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Понятие дифференциального уравнения. Метод Эйлера

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Тема занятия: «Понятие о дифференциальном уравнении. Метод Эйлера»

повторение основных понятий изученных по дисциплине «Высшая математика» по теме «Дифференциальные исчисления»: дифференциальное уравнение, порядок дифференциального уравнения, обыкновенное дифференциальное уравнение, решение дифференциального уравнения, формулировка задачи Коши;

изучение метода Эйлера для решения дифференциальных уравнений;

показать использование информационных технологий при решении дифференциальных уравнений;

показать практические применение полученных знаний в различных дисциплинах специальности: основы алгоритмизации и программирования, информационные технологии;

осуществить контроль за качеством усвоения полученных знаний по изученному материалу;

— сформировать умение осуществлять перенос знаний в измененную ситуацию.

сформировать целостную естественно научную картину специальности через предметные связи математики, информационных технологии и основ алгоритмизации и программирования;

сформировать умение видеть применение абстрактных математических понятий, в частности, математических уравнений, в других предметных областях;

развитие умения анализировать, обобщать и систематизировать материал, выделять главное из изучаемого материала;

развитие познавательного интереса и творческих способностей студентов при создании новых программных продуктов.

— воспитать уверенность в своих силах, самостоятельность при выполнении вычислений.

показать возможности использования информационных технологий; .

— показать особенности реализации межпредметного обобщения материала.

Методическое и техническое оснащение

Тип занятия: изучение нового материала.

Численные методы. Учебник для техникумов. — М .: Высшая школа, 1976.

Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике.- М.: Высшая школа, 1990.

Численные методы. Калиткин Н. Н. Главная редакция физико- математической литературы. — Наука М., 1978.

Организационный момент – 2-3 мин.

Актуализация опорных знаний.

2.1 Фронтальная беседа: (5-6 мин)

На уроках по дисциплине «Высшая математика» вами был изучен раздел «Дифференциальные исчисления». Сегодня мы вспомним этот материал и рассмотрим методы решения дифференциальных уравнений с точки зрения применения этих методов в программировании.

-Какое уравнение называется дифференциальным?

Уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называются дифференциальным уравнением.

— Что такое порядок дифференциального уравнения?

Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящей в уравнение.

— Какое дифференциальное уравнение называется обыкновенным?

Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменой, то дифференциальное уравнение называется обыкновенным.

— Какие параметры содержит в общем случае обыкновенное дифференциальное уравнение n -го порядка

Обыкновенное дифференциальное уравнение n -го порядка в самом общем случае содержит независимую переменную x , неизвестную функцию y и ее производные или дифференциалы до n -го порядка включительно и имеет вид

— Что называется решением дифференциального уравнения?

Решением (или интегралом) уравнения называется всякая дифференцируемая функция удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение оно обращается в тождество.

-Сформулируйте задачу Коши.

Задача с начальными условиями ставится так: найти решение уравнения удовлетворяющее дополнительным условиям, состоящим в том, что решение должно принимать вместе со своими производными до ( n -1)-го порядка заданные числовые значения при заданном числовом значении независимой переменной x : при

Эти условия называются начальными условиями; числа ─ начальными данными решения, а задача отыскания решения дифференциального уравнения, удовлетворяющего начальным условиям, ─ задачей с начальным условиями, или задачей Коши.

Геометрически задача Коши (для уравнения первого порядка) состоит в том, из всего множества интегральных кривых, представляющих собой общее решение, нужно найти ту интегральную кривую, которая проходит через точку с координатами

Изучение материала (60 мин)

3.1 Решение дифференциальных уравнений численными методами ( 5 мин )

Методы точного интегрирования дифференциальных уравнений, изученных вами на дисциплине «Высшая математика» пригодны лишь для сравнительно небольшой части уравнений, встречающихся на практике. Поэтому большое значение приобретают методы приближенного решения дифференциальных уравнений, которые в зависимости от формы представления решения можно разделить на две группы:

аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения;

численные методы, дающие приближенное решение в виде таблицы.

Решить обыкновенное дифференциальное уравнение численным методом – это значит для заданной последовательности аргументов и числа , не определяя функцию , найти такие значения , что и .

Таким образом, численные методы позволяет вместо нахождения функции получить таблицу значений этой функции для заданной последовательности аргументов.

Существует множество методов численного решения дифференциальных уравнений: Метод Эйлера, различные модификации метода Эйлера, метод Рунге-Кутта, метод Адамса.

Рассмотрим метод Эйлера.

3.2 Метод Эйлера (30мин)

Метод Эйлера — наиболее простой численный метод решения обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление».

Л.Эйлер (1707-1783)- математик, механик, физик и астроном, ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, теории чисел, небесной механике, математической физике, оптике, балластике, кораблестроению, теории музыки и др.

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Постановка задачи: Пусть дано обыкновенное дифференциальное уравнение первого порядка с начальным условием Требуется найти решение уравнения на отрезке [ a , b ].

Разобьем отрезок [ a , b ] на n равных частей и получим последовательностьгде, а — шаг интегрирования.

Выберем й участок [ ] и проинтегрируем уравнение :

т.е. (1)

Если в последнем интеграле подынтегральную функцию на участке принять постоянной и равной начальному значению в точке , то получим

Тогда формула (1) имеет вид

. (2)

Продолжая этот процесс и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном отрезке [ a , b ].

Все вычисления по методу Эйлера удобно располагать в таблице (см. таблицу 1). (Таблица проецируется на экран при помощи проектора с компьютера)

Таблица 1- Общая схема вычисления по методу Эйлера