Разделы: Математика
Изучение многих физических и геометрических закономерностей часто приводит к решению задач с параметрами. Очевидно, что задачи с параметрами являются задачами исследовательского характера, поэтому решение таких задач на уроках алгебры и начал анализа направлены на приобщение учащихся к активным формам получения знаний, самообучение и саморазвитие.
Как известно, в отношении уравнений с параметрами встречаются две постановки задачи.
- Решить уравнение (для каждого значения параметра найти решения уравнения).
- Найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.
При изучении курса алгебры и начал анализа, в частности в учебнике, стали появляться уравнения с параметром, а их решение сводилось к исследованию квадратного уравнения, например, уравнению вида 
- В конкретном (найденном) классе (дидактическая единица) определить возможные формулировки задач относительно количества корней рассматриваемого уравнения.
- Осуществить полный параметрический анализ в конкретном классе задач (в зависимости от параметра определить не только количество корней или наличие решения, но и записать сами корни уравнения).
В данной работе представлены четыре класса параметрических задач и возможные варианты исследования этих задач с учащимися.
- Первый класс параметрических задач “Биквадратные уравнения”
- Квадратные уравнения с параметром
- Исследование квадратного многочлена
- Уравнения с параметром — алгоритмы и примеры решения
- Общие сведения
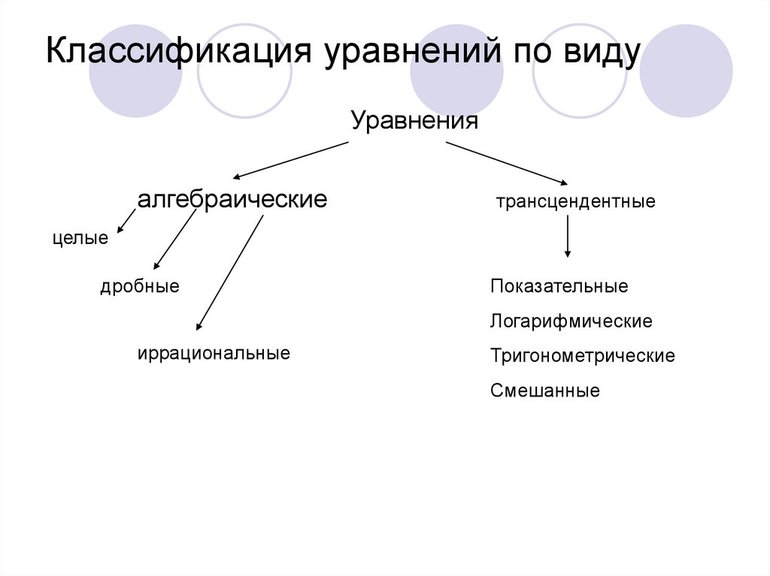
- Классификация уравнений
- Алгебраический вид
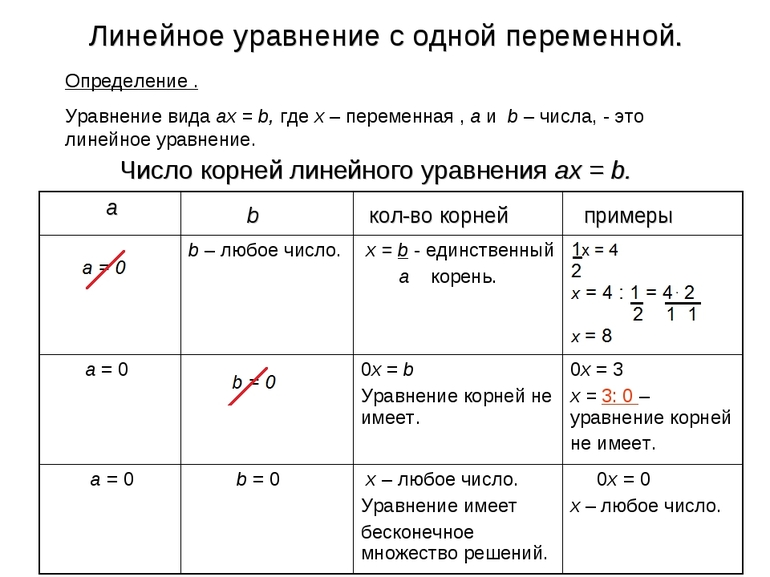
- Линейные и квадратичные
- Кубичеcкие и биквадрaтные
- Пример решения
- 📺 Видео
Первый класс параметрических задач “Биквадратные уравнения”
Рассмотрим биквадратное уравнение 
1. При каких значениях параметра a биквадратное уравнение 
Решение
Пусть 

t 2 -2at+a 2 -1=0. Корни квадратного уравнения (квадратного трехчлена) являются нулями соответствующей квадратичной функции у(t)= t 2 -2at+ a 2 -1
Геометрическая модель, отвечающая всем требованиям задачи (биквадратное уравнение имеет четыре корня), выглядит так:
То есть, для того, чтобы биквадратное уравнение имело 4 различных корня, необходимо, чтобы выполнялось следующее условие:
И мы изобразили геометрическую модель полученного условия. Теперь осталось “зафиксировать” параболу в нужном положении. Для этого перейдем от геометрической модели задачи к аналитической. Получаем систему неравенств.



Ответ: при a 
2. При каких значениях параметра а биквадратное уравнение 
Решение
Пусть 

В данном случае геометрическая модель задачи будет выглядеть следующим образом.
То есть, для того, чтобы биквадратное уравнение имело три различных корня, необходимо, чтобы выполнялось следующее условие
Составим систему алгебраических условий.

Ответ: при a=1 биквадратное уравнение имеет три различных корня.
3. При каких значениях параметра а биквадратное уравнение 
Решение.
Пусть 

То есть, для того, чтобы биквадратное уравнение имело два различных корня, необходимо чтобы выполнялось следующее условие:

Изобразим геометрическую модель полученного условия y
Составим систему алгебраических условий.




Объединяя решения двух случаев, получаем окончательный ответ.
Ответ: a
4. При каких значениях параметра а биквадратное уравнение 
Решение.
Пусть 

Для того, чтобы биквадратное уравнение имело 1 корень, необходимо, чтобы выполнялось следующее условие: t=0 (корень квадратного уравнения равен нулю).
Изобразим геометрическую модель полученного условия
Составим систему алгебраических условий.

Ответ: таких значений параметра а нет.
5. При каких значениях параметра а биквадратное уравнение 
Решение.
Пусть 

Для того, чтобы биквадратное уравнение не имело корней, необходимо, чтобы выполнялось следующее условие
Не было нулей функции или
Изобразим геометрическую модель полученного условия
Составим систему алгебраических условий.
Д
4 
Ответ: при 
Выводы по первому классу параметрических задач “Биквадратные уравнения”.
Полученная схема позволяет исследовать любое биквадратное уравнение с параметром относительно задачи, в которой необходимо найти такие значения параметра а, при каждом из которых корни уравнения удовлетворяют заданным условиям (наличие корней, количество корней и др.)
Второй класс параметрических задач “Показательные уравнения”.
Рассмотрим показательное уравнение вида 
Исследование данного уравнения сводится к квадратному уравнению относительно t, где t = 2 х .
В отличие от биквадратных уравнений, при исследовании данного класса уравнений можно выделить только три вида задач.
Рассмотрим их решение на примере рассматриваемого уравнения.
1. При каких значениях параметра а показательное уравнение 
Решение.
Пусть 


Корнями полученного квадратного уравнения являются нули функции у(t)= t 2 —
То есть, для того, чтобы показательное уравнение имело 2 корня, необходимо, чтобы нули квадратичной функции удовлетворяли условию:
Изобразим геометрическую модель поставленной задачи.
Составим систему алгебраических условий.

a
Ответ: при a 
2. При каких значениях параметра а показательное уравнение 
Решение.
Пусть 
примет вид: t 2 —
Аналогичные рассуждения приводят нас к условиям, которым должны удовлетворять корни квадратного уравнения t 2 —
1) случай: 
2) 
Каждому условию соответствует геометрическая модель (расположение параболы в системе координат).
Составим систему алгебраических условий.


То есть, для того, чтобы показательное уравнение не имело корней, необходимо чтобы выполнялось одно из следующих условий
1) квадратное уравнение t 2 —

2)
Изобразим геометрическую модель полученных условий
Решая соответствующие системы алгебраических неравенств, получим окончательный ответ.





Ответ: при a 
Выводы по второму классу параметрических задач
Во втором классе параметрических задач кроме ответа на поставленный вопрос задачи были найдены непосредственно и корни показательного уравнения. Таким образом, исследование показательного уравнения вышло за рамки поставленной проблемы (найти значения параметра а, при которых корни уравнения удовлетворяют определенным условиям).
Третий класс параметрических задач “тригонометрические уравнения”.
Как известно из курса алгебры и начал анализа, тригонометрическое уравнение, если имеет корни, то их бесчисленное множество. Поэтому, относительно корней тригонометрического уравнения, формулировки задач меняются существенным образом. А именно: при каких значениях параметра а, тригонометрическое уравнение имеет корни или не имеет корней (речь не идет о количестве корней).
Рассмотрим на конкретном примере исследование тригонометрического уравнения.
1. При каких значениях параметра а, тригонометрическое уравнение 
Пусть 



1) 
Изобразим геометрическую модель полученного условия
Составим и решим систему алгебраических неравенств.


2) 
Изобразим геометрическую модель полученного условия

3) Рассмотрим еще две геометрические модели, которые соответствуют условию существования корней тригонометрического уравнения.
А) 

Б) 

Решение.
А)
Б) 
Объединяя все три случая 1),2),3) получаем окончательный ответ.
Ответ: при а 
2. При каких значениях параметра а тригонометрическое уравнение 
Пусть 



1) 
Аналогичные рассуждения приводят к геометрической модели и соответствующей системе алгебраических неравенств.
2) Расположение корней квадратного трехчлена на координатной плоскости дает еще два случая, при которых тригонометрическое уравнение не имеет корней, а именно:


3) Тригонометрическое уравнение не имеет решений и в случае, когда квадратное уравнение не имеет действительных корней. А это возможно лишь при условии отрицательности дискриминанта. Имеем, Д = (а-2)(а -10)
(а-2)(а -10) 
Объединяя все три случая 1),2),3) получаем окончательный ответ.
Ответ: при а 
Выводы по третьему классу параметрических задач.
Из таблицы мы видим, что параметр а принимает все действительные значения, и при каждом значении тригонометрическое уравнение либо имеет решения, либо нет.
Четвертый класс параметрических задач “ Уравнения, содержащие обратные тригонометрические функции”.
При исследовании каждого класса параметрических задач, возникает вопрос: сколько и какие задачи можно решить, используя данный алгоритм. В ходе изучения курса алгебры и начал анализа особое внимание обращаю именно на те уравнения, которые встречаются в тестах ЕГЭ, в контрольных работах, которые предлагаются на вступительных экзаменах различных ВУЗов. Рассмотрим на конкретном примере еще один класс параметрических задач, а именно, уравнение вот такого вида: arccos 2 x-2aarccosx+a 2 -1=0.
Пусть arccosx = t, но из курса алгебры и начал анализа известно, что Е(t) =

1. При каких значениях параметра а уравнение arccos 2 x-2aarccosx+a 2 -1=0 имеет два корня?
Пусть arccosx = t, где t 
t 2 -2at+a 2 -1 =0. И если квадратное уравнение имеет два действительных корня, принадлежащих отрезку 

“Зафиксируем” параболу в нужном положении системой алгебраических условий (ветви параболы направлены вверх, так как первый коэффициент квадратного трехчлена положительный).
Ответ: при 
2. При каких значениях параметра а уравнение arccos 2 x-2aarccosx+a 2 -1=0 имеет один корень?
Решение.
Для данной постановки задачи приведем геометрическую модель (уравнение имеет один корень при условии принадлежности отрезку 


Объединяя случаи А), Б), В), Г) получаем окончательный ответ.
Ответ: при 
3. При каких значениях параметра а уравнение arccos 2 x-2aarccosx+a 2 -1=0 не имеет корней?
Решение.
- Если дискриминант квадратного уравнения отрицательный, то уравнение arccos 2 x-2aarccosx+a 2 -1=0 не имеет корней, но дискриминант положительный при всех значениях параметра а.
- Следовательно, геометрическая модель задачи, при которой данное уравнение не имеет корней, может иметь вид, представленный в таблице.
Объединяя три случая, представленные в таблице, получаем окончательный ответ.
Ответ: при а 
Выводы по четвертому классу параметрических задач.
Итак, в данном классе параметрических задач параметр а “пробегает” все действительные значения и, в зависимости от значений параметра, уравнение может иметь два, один, или не иметь корней. Эти выводы можно показать и в иной форме. Например, так.
В результате таких исследований учащимся удается найти и понять принципы составления класса параметрических задач. Например, можно заметить, что имеет место исследование таких уравнений, которые содержат ограниченные функции. В своих работах учащиеся рассматривали уравнения, содержащие такие функции как у= х 2 , у = 2 х , у = sinx, у= arccosx. Класс параметрических задач можно расширять, и эта проблема учащимися уже решена. Так, например, изучая и исследуя функцию с помощью производной, можно определять ограниченные функции и составлять новый класс параметрических задач. Так было с функцией 


Видео:Решение биквадратных уравнений. 8 класс.Скачать

Квадратные уравнения с параметром
Уравнение называется квадратным, если имеет вид (ax^2+bx+c=0,) где (a,b,c) — любые числа ((a≠0)). При этом надо быть внимательным, если (a=0), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при (x^2) и рассматривать 2 случая: (a=0) (линейное уравнение); (a≠0) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.
Видео:Биквадратное уравнение с параметром ( от израильского абитуриента )Скачать

Исследование квадратного многочлена
Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:
- Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2 0)); ветки параболы направлены вниз ((a 0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
- (a 0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).
В итоге получаем:
если (a*f(γ) 0), то (γ∉(x_1,x_2)).
Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0 0, \x_0
При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?
1 случай: Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.
При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.
2 случай: Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac.$$ С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac;0)∪(0;+∞)). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):
Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку ([-2;2]).
1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).
2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:
Подставляем полученные выражения в систему:
Видео:Несложное биквадратное уравнение с параметром | Параметр 132 | mathus.ru #егэ2024Скачать

Уравнения с параметром — алгоритмы и примеры решения
Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Общие сведения
Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.
Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.
Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.
Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.
Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Классификация уравнений
Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».
Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.
К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.
Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
Видео:#83 Урок 8. Рациональные уравнения с параметрами. Алгебра 8 класс.Скачать

Алгебраический вид
Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.
На основании последней характеристики они делятся на 5 типов:
- Линейные.
- Квадратные (квадратичные).
- Кубические.
- Биквадратные.
- Высших порядков.
Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.
Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Линейные и квадратичные
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:
- Записывается искомое выражение.
- При необходимости раскрываются скобки и приводятся подобные элементы.
- Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
- Правая часть сокращается на коэффициент при неизвестной.
- Записывается результат.
- Выполняется проверка посредством подстановки корня в исходное выражение.
Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.
Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:
- Записать выражение.
- Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
- Вычислить значение D (D 0 — два решения).
- При D=0 формула корня имеет такой вид: t=-В/(2А).
- Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
- Записать результат.
- Выполнить проверку по отсеиванию ложных корней.
Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.
Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.
Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.
Кубичеcкие и биквадрaтные
Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.
Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:
- Приводятся подобные элементы: 3v=0.
- Находится корень: v=0.
- Приравнивается к выражению, которое заменяли: t 3 −2=0.
- Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
- Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).
Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:
- Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
- Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
- Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
- Результат: m1=-3 и m2=3.
- Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).
Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Пример решения
На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:
- Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
- Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
- Ввести замену v 4 −16=m: m+4p+4=0.
- Вывести формулу нахождения параметра: р=-(m/4)-1.
- Подставить величину m: р=-1-(v 4 +16)/4.
- C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
- Корни: v1=[12]^(¼) и v2=-[12]^(¼).
- Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
- Результат: v1=[12]^(¼).
- Проверка: ^4−16+4=16−16=0 (истина).
Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.
Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.
📺 Видео
9 класс, 7 урок, Задачи с параметрамиСкачать

Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Биквадратное уравнение с параметромСкачать

ОГЭ 2019 ЗАДАНИЕ 21. Биквадратное уравнение.Скачать

#4 ЕГЭ. ПАРАМЕТРЫ С НУЛЯ. Дробно-рациональные уравнения с параметром, сводящиеся к линейнымСкачать

Биквадратное уравнение с параметром | Параметр №6 | ЕГЭ по математикеСкачать

Уравнения с параметром. Алгебра, 8 классСкачать

Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Биквадратное уравнениеСкачать

#141 Урок 66. Дробно-рациональные уравнения с параметрами. Алгебра 8 класс. Математика.Скачать