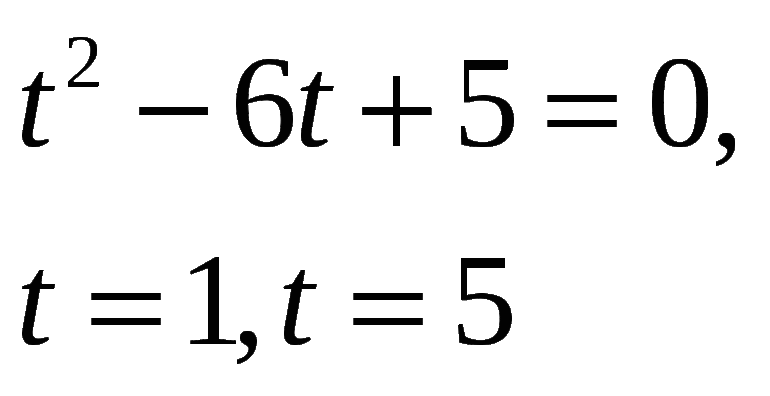Биквадратные уравнения как решать подробно

Содержание:

В самом начале напомним, что в математике принято называть уравнением. Уравнение представляет собой равенство, содержащее одну или более неизвестных величин. Решить уравнение означает найти значение неизвестной величины (или нескольких неизвестных) таким образом, чтобы их подстановка в исходное выражение давала истинное математическое равенство.

Далее подробно расскажем о биквадратных уравнениях и способах их решения. Небольшой урок по этой теме – основа, которая может оказаться неплохим подспорьем, в тот момент, когда настанет время сдавать тест по алгебре. Таким образом не приходя в школьный класс, вы сможете вполне уверенно находить решение любого биквадратного уравнения.

Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Формула биквадратного уравнения

ax 4 +bx 2 +c = 0, где

a и b – числовые коэффициенты,

с – свободный член.

При этом коэффициент «a» не должен равняться нулю.

Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Решение биквадратных уравнений

Для полной ясности рассмотрим, как решается биквадратное уравнение на примерах.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Биквадратные уравнения: примеры для решения

Сначала выполним замену переменной x2 = t и запишем новое квадратное уравнение:

Находим дискриминант для квадратного уравнения по известной формуле:

D = b 2 – 4ac = (-5) 2 – 4 ∙ 1 ∙ 4 = 9.

Напомним о том, что в случае, когда дискриминант оказывается меньше нуля, то уравнение не будет иметь корней, а когда он равен нулю, то корень будет один.

Так как полученный дискриминант D>0, то уравнение будет иметь два корня, которые найдем по формулам: t₁ = -b+D2a и -b-D2a.

Теперь задача состоит в подстановке найденных корней в формулу, по которой мы ранее изменили переменную:

x 2 = 1 и x 2 = 4.

Корни этих уравнений очевидны, но все-таки найдем их традиционным для математики способом. Для этого занесем обе части полученных равенств под знак квадратного корня:

x 2 = 1, тогда x₁ = 1 и x₂ = –1.

x 2 = 4, тогда x₃ = 2 и x₄ = –2.

Ответ. Таким образом мы получили четыре искомых корня биквадратного уравнения

Теперь рассмотрим другой пример, в котором корни биквадратного уравнения будем находить без вычисления дискриминанта. Задание будет состоять в решении уравнения:

В этом случае будет вполне логично вынести переменную x 2 за скобки, тогда получим выражение: x 2 (–9x 2 +81) = 0.

Теперь можно приравнять к нулю каждый из сомножителей уравнения.

x 2 = 0, соответственно один из корней нашего уравнения x₁ = 0.

Второе равенство решаем следующим путем:

Заносим под знак радикала обе части полученного равенства

x 2 = 9, тогда x₂ = 3 и x₃ = –3.

Ответ. Получено три корня заданного биквадратного уравнения: x₁ = 0, x₂ = 3 и x₃ = –3.

Таким образом на примерах из школьной программы мы продемонстрировали как решать биквадратные уравнения различными способами. Надеемся, что приведенная информация будет полезной при сдаче теста.

Видео:Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Видео:Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Видео:БИКВАДРАТНОЕ УРАВНЕНИЕ В ЕГЭ #shorts #математика #егэ2022 #огэ2021 #уравнениеСкачать

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю

Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.

(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)

Пример №4:
Решите биквадратное уравнение.
(x^-16=0)

Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)

Ответ: решения нет.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Биквадратное уравнениеСкачать

Биквадратные уравнения — примеры с решениями

Видео:Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Появление методики

Уравнения начали составлять ещё в Древнем Вавилоне. Это было вызвано потребностью находить площади земельных участков, выполнять инженерные работы. Составляли равенства и астрономы, высчитывая расстояния до обнаруживаемых космических тел. Квадратные равенства встречаются в клинописных текстах греков и вавилонян. При этом в этих записях попадаются уравнения, содержащие кубическую или биквадратную степень.

Несмотря на довольно хорошее развитие алгебры в стародавнее время, находимые упоминания о равенствах содержат только ответы, без указаний способов решений. Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.

В XVI веках в Китае был разработан способ нахождения корней равенств высшей степени методом Цинь Цзю-шао, после успешно применявшимся в работах Руффини и Горнера.

Этот метод использовал способ подбора, но применим был только для случаев, когда в ответе присутствовали только целые числа.

Все способы решения биквадратных уравнений сводились к приведению их к простому квадратному равенству. Была найдена формула, позволяющая решать уравнения с помощью радикалов (корней). Впервые этот метод предложил Виета, но он был рассчитан только на положительные ответы. Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.

Биквадратные выражения стали разделять на полные и неполные. В алгоритмическом языке корнями уравнения начали называть такие значения неизвестной составляющей, при которой решаемое выражение обращается в правильное числовое равенство. То есть чтобы решить задачу, нужно найти всевозможные его корни или доказать, что решения быть не может.

Видео:Урок 1. №20 ОГЭ. Биквадратные уравнения. Как делать замену, чтобы не запутаться?Скачать

Основные понятия

Биквадратным уравнением будет называться равенство вида: a*p 4 + b*p 2 + c = 0. Переменные a, b, c могут быть различными числами, при этом A не должно равняться нулю. Символ C называют свободным членом. За P принимают неизвестную переменную, требующую вычисления. Решение уравнений сводится к поиску чисел, которые при подстановке вместо P сделают равенство верным.

Согласно теореме Безу, число корней многочлена, не равного нулю, не может превосходить величину его степени. При этом любой многочлен с коэффициентами ненулевой степени должен иметь хотя бы одно решение. Тут следует отметить, что корень уравнения может быть комплексным. То есть таким выражением, степень которого равна w x = z, где x — степень, а w — комплексное число. Понятие комплексного числа уже относится к высшей математике. Обозначают его символом (z) 1/x .

Для того чтобы доказать справедливость утверждения Безу, нужно за корень многочлена f принять c1 и составить равенство f = (p — c1) f 1 . Тогда (f 1 Є K [p]), где К — является элементом поля многочлена, но лишь при условии, что f можно разделить на (p — c). Если принять за c2 корень f1, то f1 = (p — c 2)* f 2 (f 2 Є K [ p ]), а это значит что будет верным выражение: f = (p — c 1) * (p — c 2) * f2. Для длинного многочлена вида: f = (p — c 1) * (p — c 2) *…* (p — c) * s, где многочлен (s Є K [p]) не имеет решений.

Так как значения с1, с2… Cm — это все возможные корни f, то для любого поля будет верным: f (p) = (c — c1) * (c — c2)…(c — cm) * s (p). Учитывая, что s (p) не равно нулю, а f (p) = 0 только в том случае, если C равно некоторому числу I, величина корней многочлена f не может быть более значения m.

Таким образом, уравнение может иметь четыре, три, два, или одно решение. При этом есть вероятность, что ответа может совсем и не быть. Принцип, по которому решаются биквадратные уравнения, следующий:

• вводят новую переменную y = p 2 ;
• подставляют используемую переменную в решаемое уравнение;
• используя методы решения квадратных уравнений, находят корни равенства;
• найденные величины подставляют в выражение y = p 2 и вычисляют исходные корни.

Квадратные уравнения можно решать любым удобным способом. Типичная схема состоит всего из четырёх шагов и редко вызывает трудности понимания. Пожалуй, сложности могут возникнуть только при нахождении комплексных корней.

Видео:БИКВАДРАТНОЕ УРАВНЕНИЕ класс математикаСкачать

Решение равенств

Без знания методов нахождения корней в квадратных уравнениях решить самостоятельно биквадратное равенство не удастся, так как исходное неравенство в итоге приводится к виду квадратичного. Существует несколько способов, позволяющих быстро найти нужные корни или доказать невозможность существования равенства.

К основным относят:

• разложение части уравнения с неизвестной на множители;
• вынос за скобки полного квадрата;
• использование специальных формул;
• графический метод;
• теорему Виета.

Разложение многочлена на множители основано на группировании и нахождении дискриминанта, то есть знака, по виду которого можно судить о существовании корней. Для решения используется формула: a * p 2 + b * p + c = a * (p — p 1) * (p — p 2), где p и являются корнями уравнения. Этот способ понятен и используется при обучении учащихся решению задач такого типа.

Нахождение корней методом выделения полного квадрата требует опыта использования формул сокращённого умножения, особенно если коэффициентами являются рациональные числа. При решении используется выражение: (a + b) 2 = a 2 + 2* a * b + b 2 и (a — b) 2 = a 2 — 2* a * b + b 2 .

Существуют специальные формулы нахождения корней квадратного, а значит, и биквадратного уравнения. Выглядят они следующим образом: p 1 = (- b — (b 2 — 4 ac) ½ ) / (2* a) и p 2 = (- b + (b 2 + 4 ac) ½ ) / (2* a). С их помощью можно решить любое уравнение. При этом часто для упрощения решения вводят замену подкоренному выражению (b 2 — 4 ac) обозначая его буквой D — дискриминант. Если D больше нуля, то есть два корня, если меньше — решений нет. Если же D = 0, то существует только один корень.

Франсуа Виет, проводя математические исследования, смог обнаружить зависимость между корнями уравнения и его коэффициентами. Он установил, что если p1 и p2 являются решениями равенства, то их сумма будет равна второму коэффициенту с другим знаком, а произведение свободному члену. То есть для уравнения вида: p2 +r*p + k = 0, будет справедливо записать, что p1 + p2 = — r, p1 * p2 = k.

Графическое решение требует построения зависимостей. График первой представляет собой параболу, проходящую через начало координат, а второй — прямую. Для того чтобы выделить зависимости используют перенос. В результате получается две функции: y = a * p 2 и y = -(r * p+k). Построение функций и нахождение точек пересечения занимает много времени, поэтому этот метод практически никогда не используется.

Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Примеры уравнений

Решения любым из способов имеют свои достоинства и недостатки. По мнению математиков, проще решать уравнения, используя теорему Виета. Например, пусть дано выражение: 4p 4 — 5p + 1 = 0, необходимо найти все бинарные корни. В первую очередь задание нужно привести к виду квадратного равенства. Для этого вводится переменная m = p 2 . Тогда заданное уравнение можно записать как 4 m 2 — 5m + 1 = 0.

Теперь можно определить дискриминант: D = (-5) 2 — 4 * 4 * 1 = 9. Используя формулы нахождения корней, вычисляют: m1 = (5+3) / 8 = 1, m2 = (5−3) / 8 = ¼. Оба ответа удовлетворяют условию, то есть больше нуля. Подставив полученные значения в исходные выражения, решают неполные квадратные уравнения: p1 = 1; p2 = -1; p3 = ½; p4 = -½. Это цифры и будут искомыми корнями.

Довольно легко решаются уравнения с помощью метода Виета. Вероятность допущения ошибки при определении корней в этом случае стремится к нулю. Например, p 4 — 10 * p 2 + 9 = 0. Чтобы избавиться от четвёртой степени, вводят переменную p. В результате уравнение принимает вид: p 2 — 10 * p 2 + 9 = 0. Теперь можно найти корни, используя обратную теорему Виета: p 1 = 9, p 2 = 1. Так как оба ответа больше нуля, то действительными корнями уравнения будут: p 1 = 3, p 2 = -3, p 3 = 1, p 2 = -1.

Определить, что решать биквадратное уравнение не имеет смысла, можно, используя комбинаторный анализ. Например, p 4 + 11*p 2 + 10 = 0. Для его решения необходимо расписать каждые члены уравнения, используя определение равенства. Так как каждый член p 4 , 11*p 2 , 10 должен быть больше либо равен нулю, то справедливым будет выражение: p 4 + 11*p 2 + 10 > 0.

Отсюда можно сделать вывод, что p 4 + 11*p 2 + 10 решения не имеет, ведь сумма неотрицательных чисел с положительным не может быть равной нулю. И также можно разложить и доказать бесперспективность поиска для задания с одними минусами, например, -2 p 4 — 45 p 2 — 12 = 0.

Но не всегда уравнение будет иметь четыре корня. Например, p 4 +4 *p 2 — 21=0. Если принять p 2 = m, квадратное уравнение изменится до вида: m 2 +4*m -21=0, отсюда m 1 = -7, m 2 =3. Теперь нужно решить первоначальное уравнение. Первый ответ не имеет действительных корней, из второго же находят решение. Им будут корни: m 1 = (3) ½ и m 2 = -(3) ½ .

Видео:Алгебра 8. Урок 1 - Рациональное выражение и его ОДЗСкачать

Разложение на множители

Самостоятельная работа, дающаяся в школе, часто предполагает решение биквадратных равенств методом разложения на множители. Связанно это с тем, что этот способ позволяет понять принцип нахождения корней для многочлена любой степени.

Например, нужно разложить уравнение p 4 + p 3 — 6p 2 на множители. В первом действии неизвестное выносится за скобки p 2 (p 2 + p — 6). Во втором, используя формулу нахождения решений, вычисляют: p 1 = (-1 + (1 2 — 4 * (-6)) ½ ) / 2, p 2 = (-1 — (1 2 — 4 * (-6)) ½ ) / 2. Отсюда корни уравнения будут p1 = -3, p2 = 2. Подставив полученные значения в заданное выражение, можно записать: p 2 + p — 6 = (p — p 1)*(p — p 2) = (p + 3) * (p-2).

Пошагово описать разложение многочлена можно на следующем примере: p 4 + 2p 3 + 3p 2 + 4p +2. Решают его в следующей последовательности:

1. Предположив, что решение имеет хотя бы один рациональный корень, можно утверждать, что он и будет делителем второго члена. Значит, он будет любым из цифр: -2, -1, 1, 2.
2. Подставив эти числа в уравнение, получим четыре ответа: 6, 0, 12, 54. То есть одним из корней будет -1.
3. Разделив многочлен на (p- p1), запишем уравнение p 3 + p 2 + 2p + 2.
4. Теперь можно составить равенство: p 4 + 2p 3 + 3p 2 + 4p +2 = (p + 1) * (p 3 + p 2 + 2p + 2).
5. Для решения уравнения, стоящего во второй части произведения, делают предположение, что кубический многочлен имеет целый корень числа 2, а значит, его ответом будет так же -1.
6. Сгруппировав члены, можно записать: (p + 1) * p 2 + 2 * (p + 1) = (p + 1) * (p 2 + 2).
7. Из-за того, что уравнение p 2 + 2 = 0 не может иметь действительных корней, разложение будет иметь вид: p 4 + 2p 3 + 3p 2 + 4p +2 = (p + 1) 2 * (p 2 + 2).

Вычисление корней требует внимательности и усердия. Для проверки своих навыков можно использовать онлайн-калькуляторы. Это сервисы, использующие специальное программное обеспечение, часто написанное на Паскале, умеют быстро и безошибочно рассчитывать корни любого примера.

Чтобы решить биквадратное уравнение онлайн, особых умений или знаний правил не нужно. Всё, что требуется — это ввести в предложенную форму параметры решаемого равенства. Из наиболее популярных интернет-порталов выделяют Allcalc. Используя его, можно проверить свои знания, исправить допущенные ошибки при самостоятельном расчёте. Причём свои услуги сайт предлагает совершенно бесплатно.

🔍 Видео

ОГЭ 2019 ЗАДАНИЕ 21. Биквадратное уравнение.Скачать

Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Математика | Кубические уравнения по методу СталлонеСкачать

Биквадратное уравнениеСкачать

Биквадратное уравнениеСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Биквадратные уравнения. Как их решать.Скачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать