Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.
Видео:Урок 1. №20 ОГЭ. Биквадратные уравнения. Как делать замену, чтобы не запутаться?Скачать

Формула биквадратного уравнения:
Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.
ax 4 +bx 2 +c=0, где a≠0
Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Как решаются биквадратные уравнения?
Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю
Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.
(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:
Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.
Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)
Возвращаемся в замену, подставим вместо переменной t полученное число:
Можно не во всех случаях делать замену. Рассмотрим пример.
Пример №3:
Решить биквадратное уравнение.
Выносим переменную x 2 за скобку,
Приравниваем каждый множитель к нулю
Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)
Пример №4:
Решите биквадратное уравнение.
(x^-16=0)
Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)
Ответ: решения нет.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Видео:ОГЭ 2019 ЗАДАНИЕ 21. Биквадратное уравнение.Скачать

Урок по математике на тему «Биквадратные уравнения» (9 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ . ⭮? ?ࠢ. pptx
Описание презентации по отдельным слайдам:
Целое уравнение и его корни
Физкультминутка Сжать руку в кулак, разжать; Поставить ногу на пятку, на носок; Мысленно посчитать 1-2-3-4-вдох, 1-2-3-4-выдох; Закрыть глаза и мысленно сосредоточиться на одном предмете (ручка, окно, животное и т.д.).
Спасибо за урок!! «Никогда не считай, что ты знаешь все, что тебе уже больше нечему учиться. Учитесь, добывайте новые знания, и они вам всегда пригодятся».
Выбранный для просмотра документ . docx
Тема: Целое уравнение и его корни. Биквадратные уравнения (9 класс)
Бурко Татьяна Геннадьевна, лицей 35 им. Буткова В.В., г. Калининград
Данный урок является третьим из четырёх уроков, которые отводятся на изучение темы «Целое уравнение и его корни» Преподавание ведётся по учебнику «Алгебра, 9», Ю.Н. Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б. Суворова. Данная тема включена в главу «Уравнения и неравенства с одной переменной». Изучение данной темы начинается с рассмотрения понятия целого уравнения, определения степени уравнения, где рассматриваются различные виды уравнения: ах+ b =0 – уравнение первой степени, ax 2 + bx + c =0 – уравнение второй степени, ax 3 + bx 2 + cx + d =0 – уравнение третьей степени, ax 4 + bx 3 + cx 2 + d х+е=0 – уравнение четвертой степени, где а, b , с, d — некоторые числа, причем а≠0. Решение уравнения, степень которого больше двух, иногда решается введением новой переменной. Эти сведения используются при решении биквадратных уравнений. Важно, чтобы учащиеся понимали, что биквадратное уравнение можно привести к квадратному уравнению методом введения новой переменной.
Цель урока : сформировать умение решать биквадратные уравнения.
Образовательные задачи урока :
ознакомить учащихся с понятием биквадратного уравнения,
рассмотреть способ решения уравнений приводящих к квадратным уравнениям,
научить учащихся решать данные уравнения
Развивающие задачи урока:
развивать активность учащихся,
формировать учебно – познавательные действия при решении уравнений,
развивать самостоятельную деятельность учащихся.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать информационную культуру.
На данном уроке используются: презентация, сделанная в программе Power Point .
Проверка домашнего задания.
Индивидуальные и практические задания.
Постановка цели урока. Изучение нового материала.
Закрепление нового материала.
Цель: подготовка учащихся к работе на уроке.
Проверка домашнего задания.
— выяснение того, кто из учащихся справился с заданием и готов к усвоению нового материала;
— проверка правильности выполнения задания.
№ 277. Решите уравнение.
кто не справился с заданием;
кто выполнил задание;
какое выражение заменили новой переменной
какое уравнение получилось
какие корни имеет полученное уравнение
формулу нахождения дискриминанта, корней квадратного уравнения.
Открывается решение, выполненное одним из учащихся
( сделать перед началом урока).
Учащиеся называют причины затруднений при выполнении задания.
— Ввод новой переменной;
— Нахождение корней уравнения
Проверяют правильность решения задачи по предложенному образцу.
Индивидуальные и практические задания.
проверка знаний учащихся изученного ранее материала.
Индивидуальное задание слабым учащимся.
Решить квадратные уравнения с помощью формулы корней квадратного уравнения:
Задание: Решить квадратное уравнение, используя формулу корней
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя формулу корней
(корни уравнения запишите в порядке возрастания через точку с запятой)
Индивидуальные задания средним учащимся.
Найти корни квадратного уравнения по теореме Виета:
Задание: Решить квадратное уравнение, используя теорему Виета
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя теорему Виета
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя формулу корней
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя формулу корней
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя теорему, обратную теореме Виета
(корни уравнения запишите в порядке возрастания через точку с запятой)
Задание: Решить квадратное уравнение, используя теорему, обратную теореме Виета
(корни уравнения запишите в порядке возрастания через точку с запятой)
Практическая работа по подготовке к ОГЭ (остальная часть класса)
Сайт «РЕШУ ОГЭ», вариант 10309297 (5 заданий), возможна оценка.
-актуализация опыта учащихся по данной теме;
-подготовка учащихся к усвоению нового материала;
-организация целенаправленной познавательной деятельности учащихся.
— 4) Найдите корни уравнений;
— 6) Какой теоремой воспользовались при нахождении корней квадратного уравнения?
Каким способом решить данное уравнение?
Чему равен корень четвертой степени из 625?
Как решить данное уравнение? Постановка проблемы.
Теоремой, обратной теореме Виета: 3; 4.
Теоремой, обратной теореме Виета: -3; -2.
Вынесением общего множителя за скобки: 0; 1.
9) Проблемная ситуация . Учащиеся понимают, что ответ могут дать лишь наугад, так как не хватает знаний.
5. Физкультминутка. Слайд.
Упражнения для релаксации (готовимся к успешной сдаче ОГЭ по математике).
Сжать руку в кулак, разжать;
Поставить ногу на пятку, на носок;
Мысленно посчитать 1-2-3-4-вдох, 1-2-3-4-выдох;
Закрыть глаза и мысленно сосредоточиться на одном предмете (ручка, окно, животное и т.д.).
Постановка цели урока.
Изучение нового материала.
-ввести понятие биквадратного уравнения;
— рассмотреть способ решения данного уравнения;
— развивать активность учащихся.
Вы уже знаете, какое уравнение называется квадратным и как оно выглядит. Вспомните! Но есть ещё один вид уравнений (№9 в устной работе), решение которого сводится к решению квадратного. Какой?
Уравнение такого вида называется биквадратным уравнением.
Вот теперь пишем в тетрадях число, сегодня 16.11.2017, классная работа, тема урока «Биквадратные уравнения». И запишем общий вид этого уравнения.
Кто скажет, чем это уравнение отличается от квадратного? Хорошо. Но почему биквадратное? Кто знает, что означает приставка «би»? ( Два ) Посмотрите на это уравнение. Вы сказали, чем оно отличается, и приставка «би» указывает, что это уравнение как бы дважды квадратное. То есть, мы неизвестные в квадратном уравнении при старшем и втором коэффициенте возвели в квадрат и получили биквадратное уравнение. Все разобрались, уравнение какого вида называется биквадратным? ( Да )
А теперь выясним, как решаются такие уравнения. Значит, для того, чтобы решить биквадратное уравнение, необходимо ввести новую переменную , решить полученное квадратное уравнение относительно переменной , а затем вернуться к переменной .
Давайте посмотрим, как этот алгоритм применяется на практике. Сейчас я буду показывать, как правильно оформлять решение такого уравнения. Все записываем в тетрадь.
Нам дано следующее уравнение
. Это, какое уравнение? ( Биквадратное ).
Введем замену . Получили уравнение
Это, уравнение какое? ( Квадратное ). Умеем решать квадратное уравнение? ( Да ).
Решите в тетради и назовете мне корни ().
Хорошо. Но это мы нашли корни квадратного уравнения, а не биквадратного.
Пишем ниже возвращаемся к замене . К какой замене? И теперь задача свелась к решению двух уравнений. Каких? ().
Чему равны корни первого уравнения? (-1 и 1) А второго? (-2 и 2).
И теперь пишем ответ. Ответ:-2; -1; 1; 2.
Закрепление нового материала.
— выработка навыка решения уравнений;
— развивать умение обобщать, строить умозаключения, делать выводы;
— развитие творческой стороны мыслительной деятельности учащихся.
Учащимся предлагается по рядам выполнить задание: решить уравнение. Слайд.
Учитель координирует действия учащихся, помогает выполнять и обосновывать решение. Учащиеся по рядам дают ответы и записывают на доске решение.
Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Биквадратные уравнения
теория по математике 📈 уравнения
Уравнение вида ax 4 +bx 2 +c=0, где а≠0 число, называется биквадратным уравнением (приставка «би» означает «двойной»). Для решения такого уравнения применяют метод введения новой переменной, чтобы получить квадратное уравнение, решение которого легко выполняется.
Рассмотрим на примерах решение таких уравнений.
Пример №1. Решить уравнение:
В данном уравнении заменим х 2 на переменную, например а (букву для замены можно брать любую): х 2 =а. Степень данного уравнения при этом понизится на 2, получаем квадратное уравнение:
Решаем данное уравнение, например, по теореме Виета. Тогда:
Методом подбора получаем корни квадратного уравнения 9 и 16. Проверяем, что действительно 9+16=25, 916=144. Теперь переходим к нахождению корней биквадратного уравнения, которое дано по условию. Мы заменяли х 2 на а, поэтому подставляем вместо а полученные значения – это 9 и 16:
Теперь находим корни каждого из этих неполных квадратных уравнений: х 2 =9, отсюда уравнение имеет два корня ±3; х 2 =16, отсюда имеет еще два корня ±4. Следовательно, данное биквадратное уравнение имеет четыре корня: 3, -3, 4, -4.
Пример №2. Решить уравнение:
Заменим на переменную у: х 2 =у. Получим уравнение:
Найдем его корни: у1=–1, у2=4. Подставим корни вместо у и получим уравнения: х 2 =–1; х 2 =4. Видим, что первое неполное квадратное уравнение не имеет корней, а корни второго уравнения – это ±2. Значит, данное биквадратное уравнение имеет корни ±2.
Пример №3. Решить уравнение:
Выполним замену переменной: х 2 =у. Решим уравнение:
Подбором корни найти невозможно, поэтому через дискриминант получаем, что корней нет, так как дискриминант будет отрицательный. Значит и данное биквадратное уравнение тоже не имеет корней.
💥 Видео
БИКВАДРАТНОЕ УРАВНЕНИЕ класс математикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

ОГЭ по математике. Решаем уравнения | МатематикаСкачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Биквадратное уравнениеСкачать
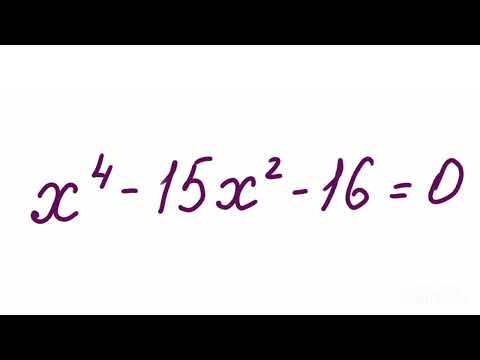
БИКВАДРАТНЫЕ УРАВНЕНИЯ | МАТЕМАТИКА | ОГЭ 2024 | 99 БАЛЛОВСкачать

ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Биквадратное уравнениеСкачать

Только 3 человека из 1000 решили это уравнение | Дробно-рациональные уравнения ОГЭ 2024Скачать

Линейные уравнения в ОГЭ | Математика ОГЭ 2022 | УмскулСкачать

Биквадратные уравнения. 8 класс алгебра.Скачать

Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Задание 20 ОГЭ математика 2024 2 часть. Кубические уравненияСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Биквадратные уравнения // Математика за 2 минуты.Скачать


