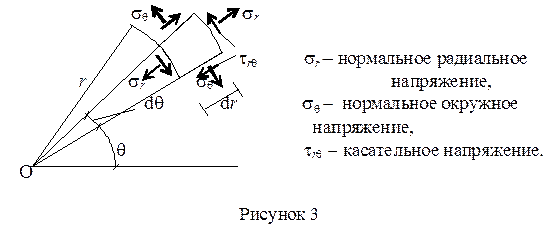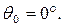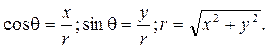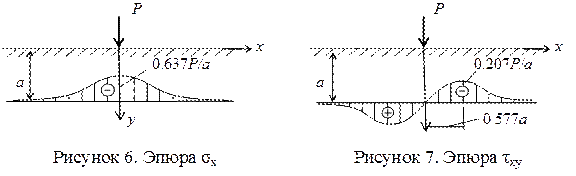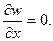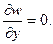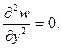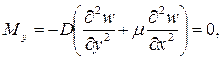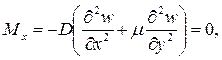Видео:Решение биквадратных уравнений. 8 класс.Скачать

Общие уравнения плоской задачи в полярных координатах
Во многих случаях, когда тело ограничено поверхностями кругового цилиндра и радиально расходящимися плоскостями, плоскую задачу теории упругости удобно рассматривать в полярной системе координат.
Совместив полюс полярной системы координат (г, 0) с началом декартовой системы координат (х, у), а полярную ось — с осью абсцисс Ох (рис. 18.1), нетрудно установить связь между координатами произвольной точки М в этих двух системах координат:
Обратные зависимости имеют вид
Уравнения плоской задачи теории упругости в полярной системе координат могут быть получены путем преобразования уравнений главы 17 с использованием зависимостей (18.1) и (18.2). Однако более просто вывести все уравнения непосредственно в полярной системе координат.
Уравнения равновесия. Выделим из нагруженного плоского тела бесконечно малый элемент abed (рис. 18.2), образованный двумя концентрическими окружностями с радиусами гиг + dm двумя лучами, проведенными под углами 0 и 0 + dQ к оси Ох. Толщину элемента примем равной единице.
На гранях ad и ab элемента действуют радиальные G r’ °9’ Х Г0 :
Сложив почленно первые две из формул (18.8) или (18.9), получим подтверждение известного свойства первого инварианта тензора напряжений при двухосном напряженном состоянии:
Уравнения неразрывности деформаций. В § 17.3 было получено уравнение неразрывности деформаций в напряжениях (17.19) в декартовой системе координат для случая, когда объемные силы постоянны или равны нулю. Это уравнение имеет вид
где
оператор Лапласа.
Для того чтобы записать оператор Лапласа в полярных координатах, установим связь между частными производными произвольной функции в декартовых и полярных координатах.
Из курса высшей математики известны формулы для определения частных производных сложной функции двух переменных:
С учетом (18.1) и (18.2) получим
Используя эти соотношения, найдем частные производные функции ср первого и второго порядка и выражение V 2 cp:
Таким образом, в полярной системе координат уравнение неразрывности деформаций плоской задачи в напряжениях для случая, когда объемные силы постоянны или равны нулю, имеет вид
оператор Лапласа в полярных координатах.
Уравнение неразрывности (18.17) и уравнения равновесия (18.3) образуют полную систему трех уравнений с тремя неизвестными
Видео:Плоская задача в напряжениях. Функция напряжений Эри.Скачать

ПроСопромат.ру
Видео:Теория упругости. Лекция №3 (1). Постановка задачи теории упругости в перемещениях и в напряжениях.Скачать

Технический портал, посвященный Сопромату и истории его создания
Видео:Лекция №1 Постановка задачи теории упругости. Условия совместности деформаций Сен-Венана.Скачать

Плоская задача теории упругости, решение с помощью функции напряжений обратным методом
Прямоугольная полоса имеет длину ℓ=10 м, высоту h=4 м и толщину, равную 1. Начало координат примем в середине левого торцевого сечения. Главными осями сечений являются оси y и z, продольная ось ОХ проходит в середине полосы-балки. Объемными силами будем пренебрегать. Функция напряжений задана в виде алгебраического полинома:
Итак, схема полосы:
Требуется:
- Проверить, может ли предложенная функция напряжений φ(х,у) быть принятой для решения плоской задачи? Для этого необходимо проверить, удовлетворяет ли она бигармоническому уравнению:
- Найти выражения для напряжений в любой точке полосы по формулам Эри:
- Построить эпюры напряжений σх и τух в заданном сечении х=2м полосы.
- Определить внешние силы (нормальные и касательные) на контуре полосы, построить эпюры этих нагрузок и указать их направления. Для этого используются условия на контуре:, где — проекции на оси ОХ и ОУ внешних сил, действующих на грани балки-полоски, — нормаль к грани, — направляющие косинусы нормали.
- Выполнить контроль полученных результатов: а) проверить, соблюдается ли закон парности касательных напряжений в углах полосы, б) составить уравнения равновесия действующих на полосу внешних сил и проверить, удовлетворяются ли они.
Решение:
1. Функция напряжений задана:
Для проверки удовлетворения бигармоническому уравнению плоской задачи ТУ вычисляем последовательно три частные производные:
Найденные частные производные подчеркнуты сплошной линией. Подставим их в бигармоническое уравнение:
Таким образом, функция напряжений удовлетворяет бигармоническому уравнению и, следовательно, может быть принята для решения плоской задачи теории упругости.
2. Найдем выражения для напряжений в любой точке полосы по формулам Эри:
3. Построим эпюры напряжений в сечении х=2м:
Судя по полученным выражениям, обе составляющие напряжений изменяются по высоте сечения полосы по законам кубических парабол. Для построения эпюр напряжений найдем их значения в нескольких точках, например, в пяти характерных точках заданного сечения х=2м. Результаты вычислений представим в таблице.
Построим эпюры напряжений:
4. Определим внешние силы (нагрузки) приложенные на контуре балки-полоски, соответствующие заданной функции напряжений:
а) нагрузки, действующие на верхнюю грань.
Уравнение верхней грани:
Значения направляющих косинусов внешней нормали:
Тогда
Для верхней грани нагрузка Хν является касательной (сдвигающей) нагрузкой.
Найдем
Yν — эта нагрузка для верхней грани является нормальной (то есть перпендикулярной к грани).
Значения ординат эпюр нагрузок на верхнюю грань приведем в таблице:
По полученным результатам строим эпюры нормальных и касательных сил, действующих по верхней грани полосы. Причем, положительные значения нагрузки Хν совпадают по направлению с осью ОХ, а положительные значения нагрузки Уν – с осью ОУ.
б) нагрузки, действующие на нижнюю грань.
Уравнение нижней грани:
Значения направляющих косинусов:
,Тогда
это для нижней грани касательная (сдвигающая) нагрузка.
А нормальная нагрузка:
Значения ординат эпюр этих нагрузок представим в таблице:
Соответствующие эпюры с указанием направлений показаны на нижней грани полосы.
в) нагрузка на левый торец.
Уравнение левого торца (грани): х=0.
Направляющие косинусы внешней нормали:
тогда:
При х=0: — это нормальная нагрузка для левой грани.
При х=0: — это касательная для левой грани нагрузка.
Значения ординат в трех точках по высоте торцевого сечения представим в таблице:
Результаты показаны в виде эпюр нормальных и касательных сил на левой грани полосы.
г) наконец, нагрузка на правый торец.
Уравнение правой грани : х=10м.
Значения направляющих косинусов внешней нормали:
Нормальная для правой грани нагрузка:
Касательная нагрузка для правой грани:
значения ординат по трем точкам правой грани представим в таблице:
Результаты показаны в виде эпюр нормальных и касательных сил на правой грани полосы.
При этом направления положительных нагрузок совпадают с положительными направлениями соответствующих им осей координат, а отрицательные – противоположны осям ОХ и ОУ.
5) Контроль полученных результатов:
а) во всех четырех углах полосы касательные силы имеют следующие направления и значения:
Результаты удовлетворяют закону парности касательных напряжений.
б) проверка равновесия полосы под действием найденных внешних сил.
(1 проверка) На ось ОХ проектируются следующие нагрузки:
— нормальная на левой грани. Ее равнодействующая, очевидно, равна нулю;
— нормальная на правой грани. Ее равнодействующая равна:
— касательная на верхней грани. Ее равнодействующая равна:
— касательная на нижней грани. Ее равнодействующая равна:
Тогда
Проверка сошлась.
(2 проверка) На ось ОY проектируются нагрузки:
-нормальная на верхней грани. Ее равнодействующая равна:
— нормальная на нижней грани. Ее равнодействующая равна:
— касательная на правом торце. Ее равнодействующая равна:
— касательная на левом торце. Ее равнодействующая, очевидно, равна нулю.
Видео:2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Плоская задача теории упругости в полярных координатах
При решении плоской задачи в полярных координатах ряд инженерных задач удается решить путем непосредственного интегрирования исходных дифференциальных уравнений. Ориентация и обозначение напряжений в полярной системе координат показаны на рисунке 3.
Основные уравнения плоской задачи теории упругости в полярных координатах имеют вид:
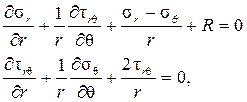
уравнение совместности деформаций в напряжениях:
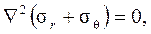
где Ñ 2 — гармонический оператор Лапласа в полярных координатах:
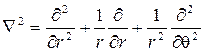
соотношения Эри и бигармоническое уравнение:

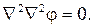
Несмотря на более громоздкий вид уравнений плоской задачи в полярных координатах для ряда инженерных задач удается найти решение в замкнутом виде.
Одной из таких задач является задача о простом радиальном напряженном состоянии, когда при интегрировании уравнений (8) и (9) получают следующее напряженное состояние:
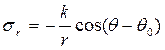
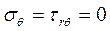
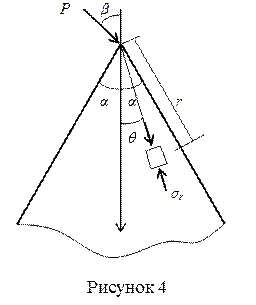
Этому состоянию соответствует задача о клине, нагруженном силой в вершине (рисунок 4).
 |
Значения постоянных k и q0, можно вычислить, воспользовавшись следующими формулами:
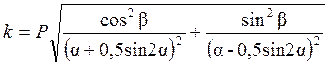
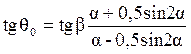
где a — угол полураствора клина и b — угол отклонения силы Р от биссектрисы угла.
Большое инженерное решение имеет частный случай — задача Фламана о действии силы на полуплоскость (рисунок 5).
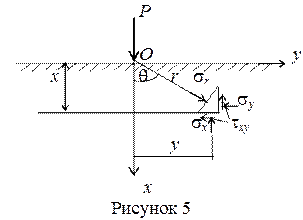 |
В этом случае угол полураствора клина равен a = 90°, угол b = 0°.
Постоянные: k =
Выражение для напряжений принимает вид:
Рассмотрим напряженное состояние полуплоскости на разных глубинах. Для этого удобнее перейти к декартовым координатам.
Воспользуемся выражениями для напряжений по наклонным площадкам:
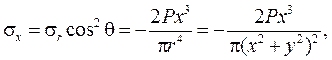
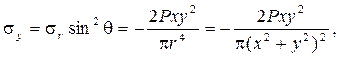
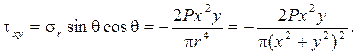
На рисунках 6 – 8 показаны эпюры напряжений в слое, отстоящем от поверхности полуплоскости на расстоянии а.
Изгиб прямоугольной пластинки
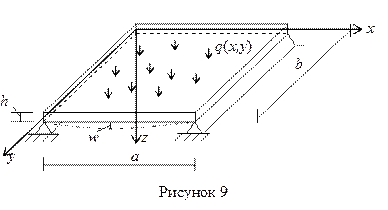
При решении задач изгиба прямоугольной пластинки (рисунок 9) функцию прогиба w(x,y) находят путем интегрирования бигармонического уравнения изгиба пластинки:
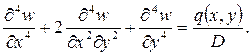
Как было указано во введении, основная и наиболее трудоемкая часть задачи расчета жесткой пластинки заключается в определении функции w(x,y) как решения бигармонического уравнения Софии Жермен — Лагранжа (19), удовлетворяющего заданной нагрузке и условиям опирания пластинки. Здесь q(x,y) –поверхностная нагрузка на пластинку; 
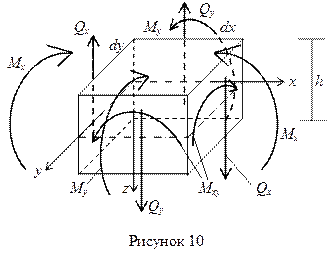
Внутренние усилия (рисунок 10) и напряжения в пластинке связаны с перемещениями следующими зависимостями.
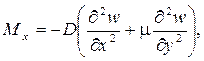
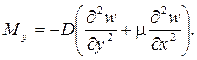
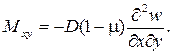
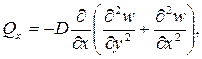
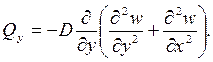
Согласно принятой в теории изгиба пластинок гипотезы Бернулли – Кирхгофа о жесткой нормали, напряжения, создающие изгибающие моменты Mx, My, определяются по формулам сопротивления материалов:
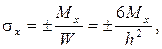
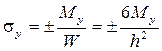
где W = 1·h 2 /6 – момент сопротивления элемента поперечного сечения пластинки единичной ширины.
Таким образом, если известна функция w(x,y), то, вычислив максимальный прогиб, можно проверить условие жесткости. Далее, определив внутренние усилия по выражениям (20) и (21), можно найти их максимальные значения и по формулам (23) вычислить наибольшие напряжения и дать оценку прочности пластинки.
Уравнение (19) имеет множество решений и для отыскания своего решения необходимо воспользоваться граничными условиями – условиями опирания пластинки.
Запись условий опирания.
В теории пластинок приняты три основных вида опирания – защемление, свободное (шарнирное) опирание и свободный неопертый край.
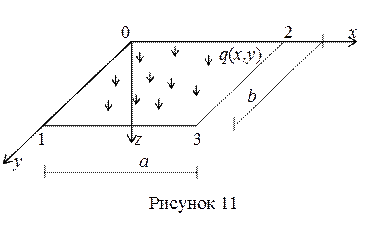
Пусть левый край пластинки 0-1 с координатами х = 0, 0 ≤ у ≤ b защемлен (рисунок 11). В этом случае граничные условия принимают вид:
2) угол поворота левой грани
Если защемлены верхний или нижний края пластинки, условия опирания имеют аналогичные выражения:
1) прогиб w = 0, 2) угол поворота нижней (верхней) грани
Верхний край 0 — 2 с координатами 0 ≤ x ≤ a, y = 0 шарнирно оперт. Тогда граничные условия записываются как:
Изгибающий момент на грани My = 0. Поскольку производная по х на верхней опертой грани 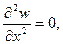
2) My =
Если шарнирно оперты боковые грани, то условия опирания имеют вид:
1) w = 0, 2) Mx =
Пусть нижний край 1-3 (0 ≤ x ≤ a, y = b ) неоперт. В этом случае w ≠ 0, а нулю должны быть равны усилия (реакции) на свободном неопертом крае. Т. е.
Два последних условия можно объединить в одно 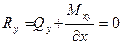
1)
2) 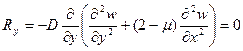
Если неоперты правый или левый край, то граничные условия запишутся как:
1)
2) 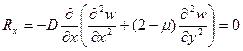
📺 Видео
Закон Гука и сила упругостиСкачать

Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать

Теория упругости. Лекция №3 (2). Пример простейшей задачи теории упругости.Скачать

Напряжения. Свободная энергия. СЕ. МКЭ. Тензор напряжений. Вектор напряжений. Теория упругости.Скачать

Уравнение с модулемСкачать

1 Решение задачи графическим и аналитическим методомСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Лекция №13 "Элементы теории упругости"Скачать

Основы Сопромата. НапряженияСкачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Вариационные принципы.Скачать

Консультация к устному экзамену. Механика. Часть 8: "Элементы теории упругости"Скачать

Уравнение плоскости. 11 класс.Скачать