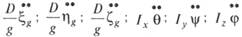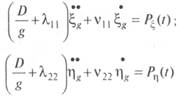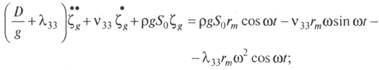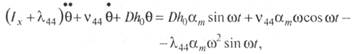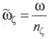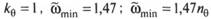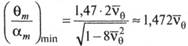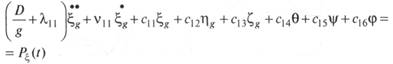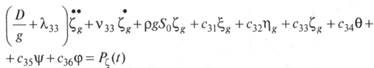Системы координат. Виды качки.Уравнения качки судов и МБУ имеют одинаковую форму. Отличаются лишь коэффициенты уравнений. Поэтому в настоящем параграфе мы обобщенно называем и суда и МБУ плавающими сооружениями. Там, где будет необходимо учитывать своеобразие в качке судов или МБУ, будем это специально подчеркивать.
Для описания движения качающегося судна или любого плавающего сооружения применяют обычно три основные системы координат.
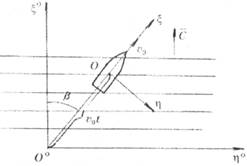
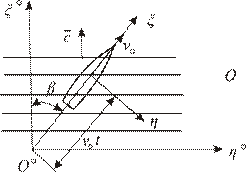
1. Абсолютно неподвижная в пространстве система координат 0 0 0 0 0 , которую мы, кстати, применяли для описания регулярного волнения (рис. 5.22). Ось 0 0 0 параллельна скорости бега волн с, ось 0 0 0 параллельна волнам, где ось 0 0 0 направлена вертикально вниз, плоскость 0 0 0 0 — невозмущенная поверхность воды.
2. Первая подвижная система координат 0. Плоскость 0совпадает с невозмущенной поверхностью воды. Ось 0^ направлена вертикально вниз. Начало координат 0 движется вместе с сооружением поступательно с постоянной скоростью v0, составляющей так
называемый «курсовой» угол со скоростью волн с.
Рис. 5.22. Первая и вторая системы координат
Если качки нет, начало координат 0 находится на одной вертикали с ЦТ сооружения и расположено в плоскости ВЛ. Ось 0 лежит в ДП и направлена в нос параллельно v0, ось 0| направлена на правый борт, плоскость 0 — плоскость ВЛ.
Ввиду того, что система координат 0 участвует только в поступательном движении сооружения и не участвует в качке, ее называют также полунеподвижной.
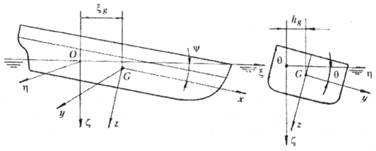
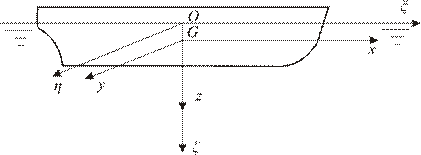
3. Вторая подвижная система координат Gxyz жестко связана с сооружением и при качке движется вместе с ним. Начало координат G лежит в ДП. Ось Gx направлена в нос, ось Gy — на правый борт, ось Gz — вниз (рис. 5.23). Система координат 0 служит для описания колебательного движения сооружения, а система координат Gxyz — для описания самого сооружения.
В соответствии с принятыми системами координат различают шесть видов качки (рис. 5.24):
1) продольно-горизонтальная качка, характеризующаяся переме-
2) поперечно-горизонтальная качках характеристиками движения
• ••
4) бортовая качка с углом крена , угловой скоростью и уг-
ловым ускорением — движение относительно оси Gx;
Рис. 5.23. Вторая и тре тья системы координат
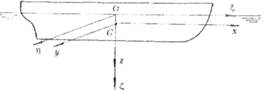
Рис. 5.24. Перемещения сооружения при качке
5) килевая качка с углом дифферента , угловой скоростью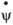 
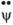
и угловым ускорением 
— движение относительно оси Gy;
6) рыскание с углом рыскания , угловой скоростью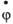 
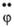
и угловым ускорением 
— движение относительно оси Gz.
Первые три вида качки — это поступательные колебательные движения сооружения вместе с центром тяжести G, последние три — вращательные колебательные движения судна относительно осей, проходящих через ЦТ.
Для сооружений, плавающих в свободном (незаякоренном, не-пришвартованном и вообще без каких-либо связей с другими объектами) состоянии, восстанавливающие силы существуют только для вертикальной, бортовой и килевой качки, поэтому эти виды качки называют основными. Другие виды качки называют дополнительными.
Продольно-горизонтальная, вертикальная и килевая качка — составляющие продольной качки — происходят в плоскости ДП, а поперечно-горизонтальная, бортовая и вертикальная — боковой (поперечной) качки, так как происходят в плоскости, перпендикулярной ДП
Классификация сил, действующих на плавающее сооружение при качке. На плавающее сооружение как на твердое тело, совершающее движение с ускорением, действуют сила веса Д а также силы и моменты, обусловленные инерцией сооружения. Их можно записать в виде
где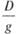 
— масса сооружения; 1x, Iy , Iz — моменты инерции массы
сооружения относительно осей Gx , Gy и Gz.
Ввиду того, что сооружение качается на поверхности воды, со стороны воды действуют силы и моменты гидромеханической природы. Они разделяются на несколько составляющих .
1. Гидростатические силывозникают как результирующие гидростатических давлений, действующих на смоченную поверхность сооружения, переменную во время качки.
В равновесном положении при отсутствии качки на сооружение
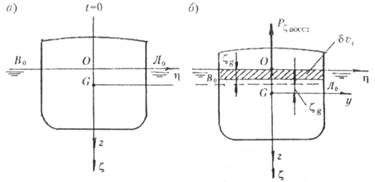
действует сила плавучести, равная Pгидростат =-gV0 ( V0— объемное водоизмещение, знак «—» выбран потому, что сила направлена вертикально вверх — против положительного направления оси 0 ). При качке в воду будут входить дополнительные объемы bvt или будет меняться форма подводного объема, вследствие чего возникнут восстанавливающие силы и моменты. Пример определения восстанавливающей силы для чисто вертикальной качки симметричного относительно мидель-шпангоута сооружения показан на рис. 5.25. В этом
объем vt = S0g . Знак «—» взят потому, что сила направлена против перемещения.
Для чисто бортовой качки
(5.88)
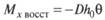
Здесь h0 — начальная поперечная метацентрическая высота.
Это выражение было получено в статике корабля, знак «—» взят потому, что восстанавливающий момент действует против наклонения.
Для килевой качки симметричного относительно мидель-шпангоута сооружения
(5.89) 189
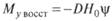
Рис. 5.25. Определение восстанавливающих сил при вертикальной качке: а — при t=0; б — в момент t
где Н0— начальная продольная метацентрическая высота.
Восстанавливающие силы, аналогичные силе сжатой пружины, линейным образом зависят от перемещений. Это верно при малых перемещениях, при больших перемещениях подобные зависимости будут давать значительные погрешности, что потребует разработки нелинейной теории.
2. Гидродинамические силывозникают в результате передачи сооружением части своей энергии окружающей воде. Некоторая доля ее тратится на придание частицам воды скоростей — возникают силы сопротивления качке, а остальная энергия расходуется на придание частицам воды ускорений — возникают силы инерции окружающей воды.
Силы сопротивления могут быть волновой природы (энергия расходуется на создание отходящих от сооружения волн) и вязкостной (энергия тратится на преодоление трения воды и на вихреобра-зование).
При малых наклонениях
(5.90)
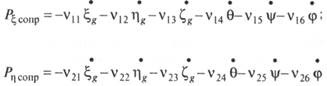
В этих выражениях: vik. — коэффициенты сопротивления; i, k — индексы, обозначающие виды качки, для которых подсчитывается сила сопротивления и который оказывает влияние соответственно.
С учетом симметрии сооружения относительно ДП и мидель-шпангоута и предположения о достаточно больших отношениях L/B и L/T можно существенно упростить выражения (5.90):
(5.91)
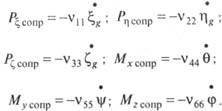
Аналогичным образом можно получить упрощенные выражения для инерционных сил:
(5.92)
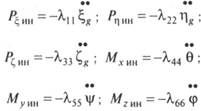
Здесь ik — присоединенные массы — мера инерции окружающей
3. Возмущающие силы и моменты.На волнении часть энергии
волн передается сооружению — действуют возмущающие силы и
моменты. Они переменны во времени. Величина их зависит от раз
меров набегающих на судно волн, размеров судна и его положения
относительно волн.
В общем виде возмущающие силы и моменты запишем как Рx(t),
4. Силы от систем позиционирования(якорных или динамичес
ких), имеют большое значение для ПБУ и буровых судов, воздей
ствуя определенным образом на сооружение. В дальнейших разделах
мы покажем, как производится учет их влияния на качку.
Общаясистема уравнений линейной качки плавающих сооружений. Качка на тихой воде. Из теоретической механики известны уравнения движения твердого тела в форме Лагранжа. Выпишем их для случая качки:
(5.93)
Если подставить все выражения для сил, действующих на сооружение, получим
; (5.94)
Силы D и gV0 взаимно уничтожаются.
Перенесем некоторые члены в левые части уравнений, оставив в правых только возмущающие силы и моменты. После приведения подобных членов линейная система уравнений качки сооружения на волнении будет иметь вид
; (5.9;5)
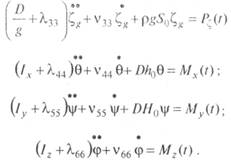
На тихой воде в правых частях уравнений получают’ся нули, так как возмущающие силы и моменты отсутствуют.
Предположим, что в какой-то момент времени на сооружение подействовало внешнее возмущение. После прекращения его воздействия оно будет испытывать качку. Вследствие отсутствия восстанавливающих сил дополнительные виды качки будут представлять собой апериодические движения (смещения), т. е. для определения качки не представляют практического интереса.
Уравнения основных видов качки можно записать как
(5.96)
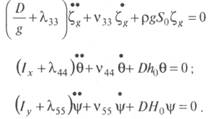
Разделим все члены уравнений на первые коэффициенты:
(5.97)
Змг.724 193
Введем новые обозначения:
а) коэффициенты затухания соответственно вертикальной, борто
вой и килевой качки
; (5.98)
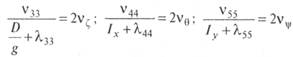
б) собственные частоты соответственно вертикальной, бортовой и
килевой качки
(5.99)
С этими частотами связаны периоды вертикальной, бортовой и килевой качки соответственно:
(5.100)
Введем безразмерный коэффициент затухания бортовой качки
(5.101)
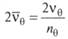
Аналогичным образом можно ввести безразмерные коэффициенты затухания вертикальной и килевой качки:
(5.102) 194
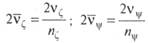
Удобство использования безразмерных коэффициентов затухания состоит в том, что они практически не зависят от размеров плавающих объектов, т. е. одинаковы и для модели и для натурного объек-та, что используется при проведении модельных экспериментов.
Сами коэффициенты затухания играют основную роль при расчетах характеристик качки на волнении, особенно резонансных амплитуд.
Обычно используются и другие безразмерные характеристики:
(5.103)
которые также не зависят от масштаба сооружения и могут определяться в модельных экспериментах.
Уравнения качки сооружений на волнении и их решение.Связь
между координатами в системах 0 0 0 0 0 , и 0 записывается в виде
; (5.104)
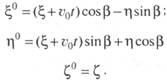
Поэтому выражение для волновой поверхности в системе координат 0 можно переписать так
(5.105) а выражение для угла волнового склона в виде
(5.106) или
(5.107)
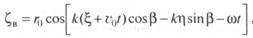
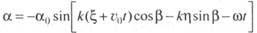
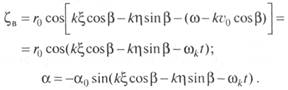
В эти выражения введена кажущаяся частота волны
, (5Л08)
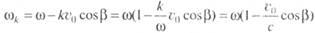
которая учитывает влияние скорости судна (сооружения) и курсового угла. Именно с такой частотой набегающее волнение и будет действовать на плавающее сооружение. Аналогичным образом,
(5.109)
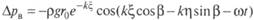
Поскольку рассматривается линейная качка, т. е. волны и перемещения сооружения при качке малы, с точностью до малых 2-го порядка малости k
kz, и поэтому выражения (5.107)—(5.109) можно переписать в виде
(5.110)
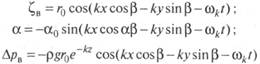
Выражения (5.110) позволяют определять возмущающие силы при набегании волнения под произвольным курсовым углом. В настоящем учебнике они приводятся без вывода.
Рассмотрим сооружение, стоящее лагом к волнению, причем волны будут набегать с правого борта. В этом случае =; k = и
(5.111)
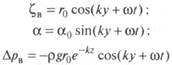
Уравнения качки сооружения конечных размеров на волнении будут иметь вид
где rт = r0 — приведенный радиус орбитального движения частиц воды; т = 0 — приведенный максимальный угол волнового склона; — коэффициенты, учитывающие конечность ширины и осадки сооружения по сравнению с длиной волны.
Эти уравнения имеют универсальный характер, так как для бесконечно малого сооружения rт —> r0, т —>0, а для сооружений больших размеров rт —> 0, т —> 0.
Первые члены правых частей уравнений называются главными (крыловскими) составляющими возмущающих сил, а вторые и третьи — дифракционными составляющими (дифракционными силами).
Решение уравнения бортовой качки получается в виде
; (5.113)
(5.114)
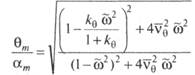
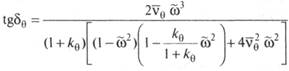
где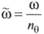 
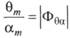
— безразмерная частота волны; 
— модуль
передаточной функции, или коэффициент динамичности, характеризующий способность сооружения как динамической системы реагировать
на внешнее возмущение; m — амплитуда вынужденной качки
сооружения на регулярном волнении; 0 — фаза колебаний судна по
отношению к колебаниям волновой поверхности.
В уравнениях для сооружений, у которых дифракционные силы малы, ими часто пренебрегают, и в результате получают, так называемые укороченные уравнения. Тогда решение упростится:
(5.115)
(5.116)
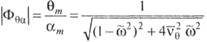
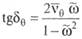
Зависимость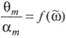 
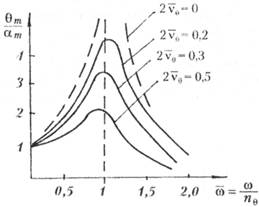
называется амплитудно-частотной
Для различных форм сооружений вид АЧХ различный. Рассмотрим некоторые из них (рис. 5.26—5.28).
На всех графиках видны зоны резонансов при со=1 или СО=я0,
т. е. при совпадении частоты волнения с собственной частотой плавающего сооружения. При этом отношение
(5.117)
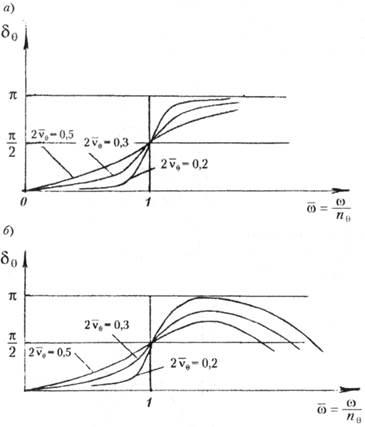
и полностью зависит от безразмерного коэффициента затухания. Зависимость 8е = /(&) называется фазово-частотной
характеристикой (ФЧХ). Ее вид при решении уравнений в форме (5.113) и (5.115) приведен на рис. 5.29.
Необходимо отметить, что для резонанса Аналогично для вертикальной качки АЧХ
, (5.118)
, (5.119)
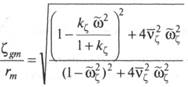
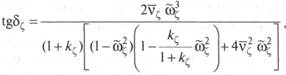
где 
Рис. 5.26. АЧХ, полученная из решения укороченного уравнени (5.115) бортовой качки судна
Рис. 5.27. АЧХ, полученная из решения полного уравнения (5.113) бортовой качки судна
Рис. 5.28. АЧХ бортовой качки ППБУ, полученная в ходе решения (5.113)
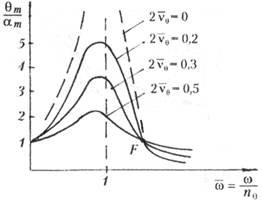
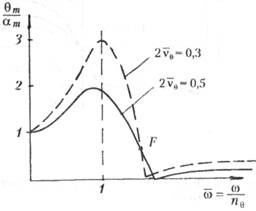
Для ППБУ соответствующие (5.118) АХЧ приведены на рис. 5.30.
Особенности качки морских буровых установок. 1. Во время перехода СПБУ вследствие своей значительной ширины имеют большие метацентрические высоты (30—40 м) и соответственно, большие собственные частоты как бортовой, так и килевой качки. Поэтому, например, для бортовой качки резонанс будет наблюдаться в зоне высоких частот (на очень коротких волнах), а качка (см. рис. 5.26) будет
Рис. 5.29. ФЧХ, полученные из решения укороченного (а) и полного (б) уравнений качки
происходить в дорезонансной зоне, где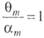 
и m =т . Если
вспомнить, что т —> 0 для сооружений больших размеров, то амплитуды бортовой качки будут всего 2—3°. Аналогично амплитуды килевой и вертикальной качки будут минимальными.
2. Наибольший интерес вызывают АЧХ для полупогружных и погружных МБУ. Для ППБУ собственные периоды бортовой качки составляют 25—40 с, волны же, обладающие максимальной энергией, имеют периоды 5—15 с. Этим волнам соответствует участок АЧХ (рис.
5.31) за (=n, т. е. минимальной качки. На этом именно и основано применение полупогружных МБУ со значительным погружением понтонов. Для них крыловская сила и инерционная часть дифракционной составляющей примерно равны, имеют обратные знаки и в значительной мере компенсируют друг друга.
Положение минимума АЧХ можно определить из (5.113), приравняв нулю скобку в числителе подкоренного выражения:
(5.120)
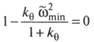
Приведя слагаемые к общему знаменателю и сделав ряд выкладок, получим
(5.121)
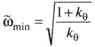
Если 
Минимальное значение отношения определяется также из (5.113):
(5.122) Если 
, то
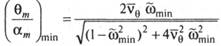
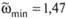
т. е. значение m в этой зоне близко к 0.
Рис. 5.30. АЧХ вертикаль ной качки ППБУ
Рис. 5.31. Определение интервала частот, в котором качка ППБУ минимальная
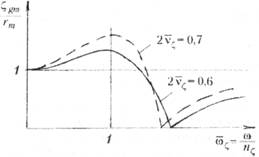
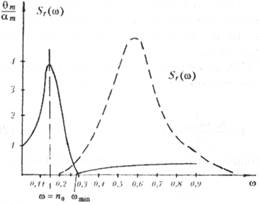
Действительно, амплитуды бортовой качки ППБУ не превышают 3—4°. Такие установки называются стабилизированными.
В процессе проектирования можно за счет изменения расстояния между понтонами ППБУ, диаметра колонн и погружения понтонов смещать зону минимальных амплитуд качки так, чтобы стабилизация установки была максимальной. Аналогичные рассуждения можно провести и для уравнений вертикальной качки. Уравнения килевой качки по форме и решению будут близки к уравнениям бортовой качки, так как обычно ППБУ симметричны относительно мидель-шпангоута, а соотношение L/B близко к 1.
Вообще же система уравнений качки ППБУ имеет гораздо более сложный вид, поэтому необходимо рассматривать все шесть видов качки при произвольном положении ППБУ относительно набегающего волнения. Эта система может решаться только с применением
современных ЭВМ. Но основные закономерности удается проследить и при проделанном нами приближенном анализе.
3. Значительное влияние на качку ППБУ оказывают якорные системы удержания. Их воздействие можно учесть в линейных уравнениях качки введением сил, связанных линейно через коэффициенты жесткости с перемещениями, например:
(5.123)
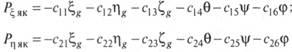
Здесь cik — элементы матрицы жесткости. Они получаются как
коэффициенты при первых производных по перемещениям в окрестности точки равновесия в формулах для сил удержания от якорных связей (см. параграф 5.3).
В общем случае раскладки якорей (несимметричная раскладка, смещенное под действием внешних сил положение и т. д.) невозможно упростить эту матрицу, поэтому в уравнения качки она должна войти полностью. Общая система уравнений качки будет иметь вид
Из (5.124) можно сделать следующие выводы:
1) дополнительные виды качки также становятся основными, так как для них будут существовать восстанавливающие силы и моменты от якорных цепей;
2) уравнения качки невозможно разделить, т. е. все виды качки будут оказывать влияние друг на друга.
Но обычно наиболее сильное влияние оказывает поперечно-горизонтальная качка на бортовую или продольно-горизонтальная качка
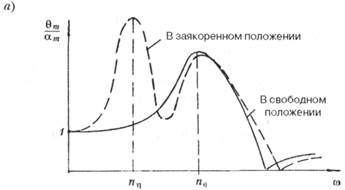
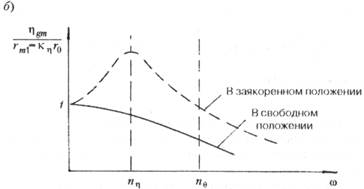
на килевую. В качестве примера на рис. 5.32 приведена АЧХ для бортовой и поперечно-горизонтальной качки ППБУ в свободном или закрепленном положении. Необходимо отметить, что для бортовой качки может появиться второй резонанс, связанный с резонансом поперечно-горизонтальной качки, причем более значительный, чем основной. Раскачать судно могут длинные волны (тягуны) или силы, возникающие при изменении ветровой нагрузки. Такая ситуация может представлять большую опасность, так как чаще всего является неожиданной.
На элементы матрицы жесткости большое влияние оказывает наравне с весомостью цепи и ее длиной также положение клюзовых точек на установке.
Рис. 5.32. АЧХ бортовой (а) и поперечной-горизонтальной качки (б) свободной и заякоренной ППБУ
Видео:Мореходные классы. Остойчивость и поперечная качка.Скачать
СИСТЕМЫ КООРДИНАТ. ВИДЫ КАЧКИ
Для описания движения качающегося судна применяются обычно 3 основ-ные системы координат.
1. Абсолютно неподвижная в пространстве система координат 0 0 x 0 h 0 z 0 (рис. 3.1), которую мы, кстати, применяли для описания регулярного волнения. Ось 0 0 x 0 параллельна скорости бега волн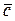 
, ось 0 0 h 0 параллельна фронту волн, ось 0 0 z 0 направлена вертикально вниз, плоскость 0 0 x 0 z 0 — невозмущенная поверхность воды.
2. Первая подвижная система координат 0xhz. Плоскость 0xh совпадает с невозмущенной поверхностью воды. Ось 0z направлена вертикально вниз. Начало координат 0 движется вместе с кораблем поступательно с постоянной скоростью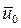 
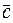
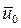
. Угол b между скоростями 
и называется «курсовым».
Рис. 3.1. Первая и вторая системы координат
Если качки нет, начало координат 0 находится на одной вертикали с центром тяжести (ЦТ) корабля и расположено в плоскости ватерлинии (ВЛ). Ось 0x лежит в диаметральной плоскости (ДП) и направлена в нос параллельно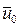 
, ось 0h направлена на правый борт, плоскость 0xh — плоскость ВЛ.
Ввиду того, что система координат 0xhz участвует только в поступательном движении корабля и не участвует в качке, ее называют также полунеподвиж-ной.
3. Вторая подвижная система координат Gxyz жестко связана с кораблем и при качке движется вместе с ним. Начало координат – центр тяжести корабля G лежит в ДП. Ось Gx направлена в нос, ось Gy — на правый борт, ось Gz — вниз (рис. 3.2). Система координат 0xhz служит для описания колебательного движения корабля, а система координат Gxyz — для описания самого корабля.
Рис. 3.2. Вторая и третья системы координат
В соответствии с принятыми системами координат существует 6 видов качки (рис. 3.3):
1) продольно — горизонтальная качка — поступательное колебательное движение корабля вместе с ЦТ по направлению оси 0x. Характеризуется перемещением ЦТ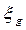 
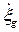
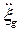
, скоростью перемещения 
и ускорением 
. Положительное направление движения в нос;
2) поперечно — горизонтальная качка — поступательное колебательное движение корабля вместе с ЦТ по направлению оси 0h.Характеризуется соответственно перемещением ЦТ, скоростью и ускорением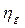 
, 
, 
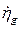
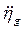
. Положительное направление движения на правый борт;
3) вертикальная качка – поступательное колебательное движение по направлению оси 0z. Характеризуется соответственно перемещением ЦТ, ско-ростью перемещения и ускорением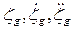 
. Положительное направление движения вниз;
4) бортовая качка – вращательное колебательное движение относительно оси Gx. Характеризуется углом крена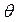 
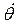
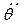
, угловой скоростью 
и угловым ускорением 
. Положительное наклонение происходит на правый борт;
5) килевая качка – вращательное колебательное движение относительно оси Gy с углом дифферента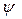 
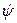
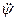
, угловой скоростью 
и угловым ускорением 
. Положительное наклонение происходит на корму;
6) рыскание – вращательное колебательное движение относительно оси Gz с углом рыскания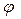 
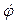
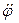
, угловой скоростью 
и угловым ускорением 
. Поло-жительное движение при рыскании происходит направо.
Пользуясь терминологией, известной из теоретической механики, можно
сказать что, первые три вида качки – это переносное движение корабля вместе с центром тяжести G , а последние три – относительное движение корабля относительно осей, проходящих через ЦТ.
Для кораблей, плавающих в свободном (незаякоренном, непришвартован-ном, и вообще, без каких-либо связей с другими объектами) состоянии, восстанавливающие силы существуют только для вертикальной, бортовой и килевой качки, поэтому эти виды качки называют основными. Другие виды качки называются дополнительными.
Рис. 3.3. Перемещения корабля при качке
Продольно-горизонтальная, вертикальная и килевая качка в комплексе называются продольной качкой (происходят в плоскости ДП), а поперечно-горизонтальная, бортовая и вертикальная – называются в комплексе боковой (поперечной) качкой, так как происходят в плоскости, перпендикулярной ДП.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать
Качка судов.Вывод уравнения вертикально качки судна без хода. Вывод уравнения бортовой качки судна без хода. Основные характеристики качки,способы ее умерения
Качкой судна называются колебательные движения, совершаемые судном относительно положения равновесия. В основном качка возникает под действием гидродинамических сил, обусловленных возмущающим эффектом ветрового волнения.
Вертикальной качкой судна на тихой воде называют поступательные движения судна вдоль вертикальной оси, вызывающие попеременное уменьшение и увеличение осадки. Вертикальная качка, как самостоятельный вид колебательных движений, возможна только в том случае, если Ц.Т. входящего в воду слоя будет находиться на одной вертикали с Ц.Т. судна. Это условие практически неосуществимо, пэтому вертикальная качка обязательно сопровождается
килевой. Периоды собственных колебаний вертикальной и килевой качки на тихой воде практически равны.
Бортовая качка. Бортовой качкой на тихой воде называют вращательное колебательное движение судна вокруг продольной оси с попеременным креном на левый и правый борта. Такую качку можно вызвать перебежкой людей по палубе с борта на борт, быстрым выносом груза стрелой или краном за борт . Бортовая качка судна на тихой воде характеризуется амплитудой бортовой качки θmи периодом собственных колебании Тθ:
Тθ = 2 × C × B / √h, Где С = 0,36 — 0,43 — коэффициент, значение которою зависит от типа
судна; В — ширина судна; h — метацентрическая высота. Это выражение называется капитанской формулой. Хотя ее точность относительно невелика, она, благодаря своей простоте, широко
применяется, например, для определения метацентрической высоты судна по
периоду бортовой качки Тθ.Анализируя эту формулу, можно сделать вывод, что период бортовой качкина тихой воде не зависит от ее амплитуды. При этом увеличение остойчивости судна уменьшает период качки судна, т.е. чем больше метацентрическая высота h, тем меньше период качки Тθ.
Успокоителями качки принято называть устройства, которые применяются для уменьшения амплитуды качки судна.Действие установленных на судне успокоителей качки состоит в том, что
они создают переменный стабилизирующий момент, противоположный по знаку возмущающему моменту волны. В настоящее время применяются успокоители только бортовой качки. Уменьшить амплитуды килевой и вертикальной качки с помощью успокоителей практически трудно, т.к. еще не созданы успокоители, способные развивать значительно большие, чем при бортовой
качке, стабилизирующие моменты.
Успокоители качки делятся на пассивные и активные. Действие рабочих
органов пассивных успокоителей основано на создании стабилизирующего
момента за счет колебательных движений судна во время качки, т.е. при их
использовании отпадает необходимость в специальных источниках энергии. В
активных успокоителях переменный стабилизирующий момент создается
принудительно с помощью особых механизмов, управляемых специальным
регулирующим устройством, которое, в свою очередь, реагирует на
колебания судна. Активные успокоители более эффективны, но на их работу
нужно затрачивать дополнительную мощность.
Пассивные успокоители. К числу пассивных успокоителей качки относятся скуловые кили и пассивные успокоительные цистерны.
Скуловые кили являются наиболее простым и эффективным средством уменьшения бортовой качки и потому находят самое широкое применение.Пассивные успокоительные цистерны могут быть двух типов: закрытого, не сообщающегося с забортной водой (I рода) и открытого, сообщающегося с забортной водой (II рода). Цистерны наполовину заполнены водой (иногда, топливом) и соединены каналами. Пассивные успокоительные цистерны наиболее эффективны при резонансной качке. При некоторых условиях и режимах нерегулярного волнения такие успокоители могут привести к увеличению амплитуд качки. Наличие свободной поверхности
жидкости в цистернах также неблагоприятно влияет на остойчивость судна. Вследствие указанных причин пассивные цистерны в настоящее время практически не используются.
Активные успокоители. К активным успокоителям качки относятся бортовые управляемые рули, активные успокоительные цистерны и гироскопические успокоители-стабилизаторы.
Бортовые
управляемые рули являются весьма эффективным средством уменьшения бортовой качки и получили широкое распространение на транспортных и особенно на пассажирских судах. Они размещены на специальных приводах, обеспечивающих изменение углов атаки по определенному закону, выдвижение их из корпуса и уборку внутрь корпуса. Практика показывает, что бортовые рули целесообразно применять при скоростях, превышающих 10-15 узл. В этом случае бортовые рули приводят к значительному (в несколько раз) снижению амплитуд бортовой качки.
Активные успокоительные цистерны обычно выполняют в виде цистерн I рода. Для регулирования движения воды применяют либо насосы, установленные в водяном канале, либо воздуходувы, расположенные в воздушном канале. Управление насосом или воздуходувкой осуществляется с помощью специальной автоматики таким образом, чтобы можно было
регулировать подачу воды из одной цистерны в другую и обеспечивать требуемое изменение стабилизирующего момента. Эффективность установки независит от скорости судна: цистерны одинаково умеряют качку на ходу и на стоянке. Недостатки активных цистерн: сложность конструкции, высокая стоимость, применение сложной регулирующей аппаратуры, снижение грузоподъемности судна необходимость затрат дополнительной энергии.
Гироскопический успокоитель качки представляет собой мощный гироскоп, вращающийся на оси в раме. Гироскоп устанавливают вертикально. Крен судна при бортовой качке вызывает поворот оси гироскопа — так называемую прецессию гироскопа. Вследствие этого возникает гироскопический момент, который является стабилизирующим моментом успокоителя. Гироскопические успокоители могут быть как пассивными, так и активными. У пассивного успокоителя прецессия возникает как реакция на качку судна. В активных успокоителях прецессия создается принудительно за счет передачи внешней энергии электродвигателю, управляемому автоматическим регулятором, реагирующим на режим качки судна. Недостатки: значительная масса, большая стоимость,сложность устройства и эксплуатации.
📸 Видео
Решаем ВСЕ уравнения из сборника Ященко | Parta 2023 | Базовая математикаСкачать
Как строить структурные формулы быстро, как ФЛЭШ — Мое полное РуководствоСкачать
ДАЛА КАЧКУ НА БЕРЕГУ/ЛЮДИ В ШОКЕ 😨 #дала #качку #юморСкачать
Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать
5.4 Уравнение гармонических колебанийСкачать
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
МЕГА СИЛА! СТАЛ САМЫМ БОЛЬШИМ КАЧКОМ В МИРЕ! СИМУЛЯТОР КАЧКА В ROBLOXСкачать
😱 КАК Мой ДРУГ Стал *НЕРЕАЛЬНЫМ* КАЧКОМ в Майнкрафт ?! Симулятор Качка ВЛАДУССкачать
Качки - КВН Уральские ПельмениСкачать
ТОП 3 ВОЗРАСТНЫХ БОДИБИЛДЕРА! #шортс #тикток #бодибилдинг #качкиСкачать
2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать
Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать
Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать
СТАЛ САМЫМ СИЛЬНЫМ В МИРЕ! СИМУЛЯТОР КАЧКА В ROBLOXСкачать
Курс химии для первоклашки.Скачать
1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать
Уравнение колебания струны. Решение методом ДаламбераСкачать
