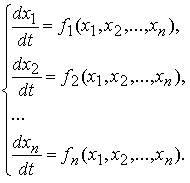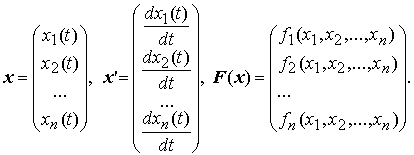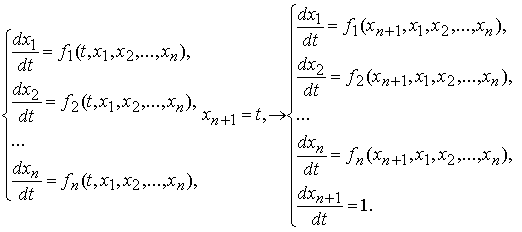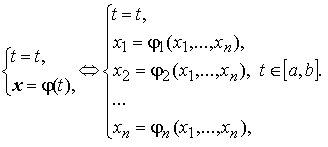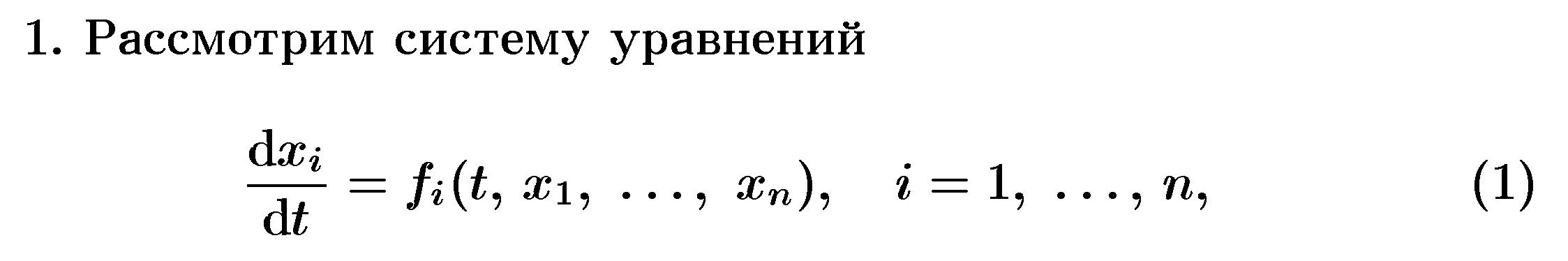Автономная система дифференциальных уравнений это

АВТОНОМНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ

Высшая математика

n –го порядка называется система, которая в нормальной форме записывается в виде

В векторной форме автономная система имеет вид x‘ = F(x) (не зависит от t), где

Название автономная система связано с тем, что поскольку производная x‘ зависит только от x и не зависит от t, то решение само управляет своим изменением. Автономные системы называют также динамическими системами.

Любую систему дифференциальных уравнений, записанную в нормальной форме, можно свести к автономной системе, увеличив число неизвестных функций на единицу:

Будем полагать, что для рассматриваемых автономных систем выполнены условия теоремы существования и единственности решения задачи Коши.

Пусть x = φ( t ) — решение автономной системы, определенное на отрезке [ a , b ] . Множество точек x = φ( t ) , t ∈ [ a , b ] — кривая в пространстве R _x n . Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство R _x n , в котором расположены фазовые траектории, называют фазовым пространством автономной системы .

Точка a называется положением равновесия ( точкой покоя ) автономной системы, если F ( a ) = 0 .

Равенство x = φ( t ) , t ∈ [ a , b ] — параметрические уравнения фазовой траектории.

Интегральная кривая системы изображается в ( n + 1) –мерном пространстве R_{x, t} n+1 и может быть определена уравнениями

Ясно, что соответствующая фазовая траектория — проекция интегральной кривой на пространство R_x .

На рисунке приведено изображение интегральной кривой автономной системы и соответствующей фазовой траектории.

Автономные системы. Свойства.

Автономной системой дифференциальных уравнений n –го порядка называется система, которая в нормальной форме записывается в виде

В векторной форме автономная система имеет вид x‘ = F(x) (не зависит от t), где

Название автономная система связано с тем, что поскольку производная x‘ зависит только от x и не зависит от t, то решение само управляет своим изменением. Автономные системы называют также динамическими системами.

Любую систему дифференциальных уравнений, записанную в нормальной форме, можно свести к автономной системе, увеличив число неизвестных функций на единицу:

Будем полагать, что для рассматриваемых автономных систем выполнены условия теоремы существования и единственности решения задачи Коши.

Пусть x = φ( t ) — решение автономной системы, определенное на отрезке [ a , b ]. Множество точек x = φ( t ) , t ∈ [ a , b ] — кривая в пространствеR_x n . Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство R_x n , в котором расположены фазовые траектории, называют фазовым пространством автономной системы.

Точка a называется положением равновесия (точкой покоя) автономной системы, если F(a) = 0 .

Равенство x = φ( t ) , t ∈ [ a , b ] — параметрические уравнения фазовой траектории.

Интегральная кривая системы изображается в ( n + 1) –мерном пространстве R_{x, t} n +1 и может быть определена уравнениями

Ясно, что соответствующая фазовая траектория — проекция интегральной кривой на пространство R_x.

Свойства: Если — решение автономной системы дифференциальных уравнений (в векторном виде), то эта функция остаётся решением и при сдвиге аргумента. Автономная система моделирует автономные процессы, т.е. процесс, не подверженные внешним влияниям, и стационарные процессы, т.е. процессы, установившиеся во времени. Все эти процессы полностью определяются начальными значениями переменных состояния, т.е. , и не зависят от выбора начального значения аргумента .

38) Положения равновесия. Циклы.

39) Особые точки. Узлы, центр, седло.

40) Основные понятия устойчивости по Ляпунову.

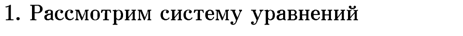
41) Устойчивость линейных систем.
Для линейной системы

x′ = A(t)x + b(t),

(ЛС)

aij, bi ∈ C([t0, +∞), R),

и любого ее решения x = φ(t) приведенная система совпадает с соответствующей (ЛОС).

Д о к а з а т е л ь с т в о. Произведем замену y = x – φ(t):

y′ = A(t)x + b(t) – A(t)φ(t) – b(t) = A(t)(x – φ(t)) = A(t)y.

Критерии устойчивости (ЛС). Пусть Φt0(t) — фундаментальная матрица (ЛОС), нормальная в t0. Утверждается, что

(а) (ЛС) устойчива ⇔ Φt0(t) ограничена на [t0, +∞);

(б) (ЛС) асимптотически устойчива ⇔ Φt0(t) → 0 при t → +∞ ⇔ (ЛС) асимптотически устойчива в целом;

(в) (ЛС) экспоненциально устойчива ⇔ (M > 0, γ > 0) ∀ (t ≥ t0) [||Φt0(t)|| ≤ Me –γ(t–t0) ] ⇔ (ЛС) экспоненциально устойчива в целом.

Д о к а з а т е л ь с т в о. (а) Пусть (ЛС) устойчива, т. е. устойчиво нулевое решение (ЛОС). Положив в определении устойчивости ε = 1, найдем δ > 0 такое, что

||x0|| t (x0)||= ||Φt0(t)x0|| t (x0)||≤ H||x0||,

так что для любого ε > 0 в определении устойчивости нулевого решения (ЛОС) можно взять δ = ε/H.

(б) Пусть (ЛС) асимптотически устойчива. Тогда ||x0|| n , поэтому, возможно, ||ek|| ≠ 1). Это означает, что все столбцы матрицы Φt0(t) стремятся к нулю при t → +∞; но тогда и сама матрица стремится к нулю.

Пусть дано, что Φt0(t) → 0 при t → +∞. Тогда для любого x0 ∈ R n

gt0 t (x0)= Φt0(t)x0 → 0 при t → +∞,

т. е. (ЛС) асимптотически устойчива в целом.

Наконец, из асимптотической устойчивости в целом следует асимптотическая устойчивость.

(в) Если (ЛС) экспоненциально устойчива, то существуют Δ₁ > 0, M > 0 и γ > 0 такие, что

||x0|| –γ(t–t0) ||x0|| (t ≥ t0).

Поэтому для любого x, удовлетворяющего условию ||x|| = 1, будем иметь:

||Φt0(t)x|| = Δ1 || Φt0(t) ( x· Δ1 ) || ≤ ≤ Δ1 Me –γ(t–t0) || x0· Δ1 || = Me –γ(t–t0) ||x||. ||Φt0(t)|| ≤ Me –γ(t–t0) (t ≥ t0). Наоборот, если выполнено последнее неравенство, то для любого x0 ||Φt0(t)x0|| ≤ ||Φt0(t)||·||x0|| ≤ Me –γ(t–t0) ||x0|| (t ≥ t0), т. е. (ЛС) экспоненциально устойчива в целом. Остается заметить, что экспоненциальная устойчивость в целом влечет экспоненциальную устойчивость. 42) Теорема Ляпунова об устойчивости по первому приближению. 43) Интегрирование линейного однородного уравнения в частных производных первого порядка. 💡 Видео Дифференциальные уравнения 3. Автономные системыСкачать Решение автономных систем дифференциальных уравнений Ланчестера и Лоттки-ВольтерраСкачать Видеоурок "Системы дифференциальных уравнений"Скачать Решение системы дифференциальных уравнений методом ЭйлераСкачать Системы дифференциальных уравнений. Часть 2Скачать Устойчивость 1 ОпределениеСкачать Системы дифференциальных уравнений. Часть 1Скачать Откуда появляются дифференциальные уравнения и как их решатьСкачать ОДУ. 4 Системы дифференциальных уравненийСкачать Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать Системы дифференциальных уравненийСкачать Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать Система дифференциальных уравнений. Операционный методСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства