Апериодическое звено второго порядка дифференциальное уравнение

3.4 Апериодическое звено второго порядка

Апериодическое звено выведем на уже известном примере. Мы разбирали вывод уравнений динамики демпфера в этой лекции. Но повторенье — мать ученья. Сначала будет много жесткой математики, а в конце наглядные модели.

У нас есть модель механического демпфера. Это поршень на пружине, он движется внутри цилиндра, может перемещается вверх-вниз. Его положение – это интересующая нас функция Y(t), сверху на него воздействует возмущающая сила (U(t)), на стенках поршня действует сила вязкого трения. (См. рис. 3.4.1)

Рисунок 3.4.1. Расчетная схема амортизатора.

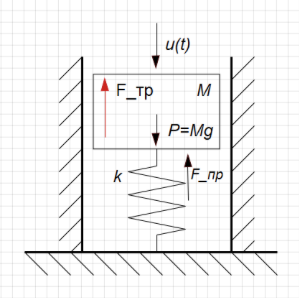
Выведем передаточную функцию для этого звена. Согласно 2-му закону Ньютона ускорение тела пропорционально сумме сил, действующих на тело:

— масса поршня;

— положение поршня (выходная переменная);

— приложенная сила (входное воздействие);

— сила тяжести;

– сила сопротивления пружины;

– сила вязкого трения (пропорциональная скорости движения поршня).

Считаем, что в нулевой момент времени поршень находится в равновесии. Тогда начальное положение поршня — y₀ в равновесии, где скорость и ускорения равны 0, можно посчитать из уравнения 2.

Перепишем уравнение равновесия в отклонениях от нулевого состояния:

Поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим:

Приведем данное уравнение к классическому виду:

Уравнение динамики апериодического звена 2−го порядка имеет следующий вид:

Если D 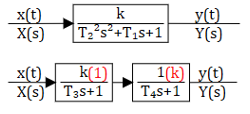Рисунок 3.4.2 Апериодическое звено 2-го порядка (два варианта)

Амплитудно-фазовая частотная характеристика (АФЧХ):

Домножив числитель и знаменатель формулы (3.4.5) на комплексно-сопряженные скобки и , получаем:

Действительная и мнимая части передаточной функции:

Анализируя поведение и при и при , получаем:

Модуль АФЧХ (амплитуда), то есть mod(W(i·ω)) = |W(i·ω)| из формулы 3.4.5:

Подставляя в формулы (3.4.6) или в формулу (3.4.5) различные значения ω можно построить векторы, соответствующие различным значениям ω:

Рисунок 3.4.3 Годограф АФЧХ апериодического звена 2-го порядка

Из формул 3.4.6 очевидно, что на рисунке годографа 3.4.3 :

omega_5>omega_4>omega_3>omega_2>omega_1>0\ 2) 0 >varphi_1>varphi_2>varphi_3>varphi_4>varphi_5>varphi_6″ alt=»1) omega_6>omega_5>omega_4>omega_3>omega_2>omega_1>0\ 2) 0 >varphi_1>varphi_2>varphi_3>varphi_4>varphi_5>varphi_6″ src=»https://habrastorage.org/getpro/habr/upload_files/663/02f/0f1/66302f0f16e854680e603612571bc0af.svg» width=»733″ height=»44″/>

Используя формулу 3.4.6 можно показать что при

Из рисунка видно, что .

Формула фазового сдвига:

omega_3 Rightarrow j=1.» alt=» omegaleq omega_3 Rightarrow j = 0;\ omega>omega_3 Rightarrow j=1.» src=»https://habrastorage.org/getpro/habr/upload_files/ee5/e65/0f3/ee5e650f39001b205a1e75c0ca3f70a8.svg» width=»733″ height=»40″/>

Для фазового сдвига удобно представить апериодическое звено в виде последовательного соединения двух звеньев (см. рис. 3.4.2). Известно, что при последовательном соединении звеньев общий сдвиг фазы равен сумме фазовых сдвигов:

Логарифмическая амплитудная характеристика (ЛАХ)

Графики А(ω), φ (ω), Lm(ω) имеют вид:

Рисунок 3.4.4 АЧХ и ФЧХ апериодического звена 2-го порядка Рисунок 3.4.5 ЛАХ и ЛФЧХ апериодического звена 2-го порядка

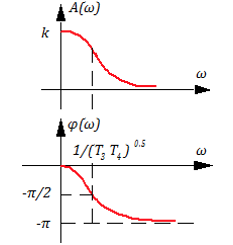
В инженерных расчетах часто график Lm(ω) представляют виде отрезков ломаных, тогда:

при — звено близко к идеальному усилительному звену

при — звено близко к идеальному интегрирующему звену

при 1/T_3″ alt=»omega>1/T_3″ src=»https://habrastorage.org/getpro/habr/upload_files/230/304/ad3/230304ad37f36d023cf3233756aa804a.svg»/>- звено близко к дважды интегрирующему звену

В граничном случае или отмеченные на графике Lm(ω) (см. рис. 3.4.5 выше) точки «излома» совпадают:

Рисунок 3.4.6 ЛАХ и ЛФЧХ апериодического звена 2-го порядка в граничном случае

Если звено “переходит” в разряд колебательных звеньев. Поэтому постоянная Т₁ в уравнении динамики (3.4.1) играет роль демпфирующего фактора, увеличение Т₁ (в колебательном звене) приводит к уменьшению или к полному исчезновению колебаний.

Найдем переходную функцию звена — реакцию на воздействие единичное воздействие 1(t).

Для нахождения функции по формуле Хэвисайда (см. раздел 2.8 Некоторые способы нахождения оригинала по известному изображению), запишем корни полюса изображения, т.е. те значения «s» при которых обращается в ноль:

Тогда по формуле Хэвисайда:

Вычисляя пределы получим формулу для переходной функции звена:

Весовая функция получается дифференцированием :

Рисунок 3.4.7 Переходная функция апериодического звена 2-го порядка

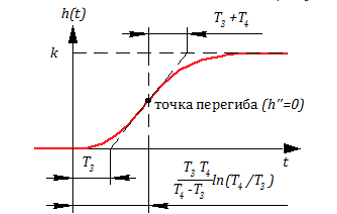
Примерами апериодического звена 2-го порядка являются:

1) двигатель постоянного тока при учете инерционности самого якоря (механической) и цепи якоря (электрической);

2) электрический усилитель руля автомобиля с учетом инерционности (механической и электрической) ротора;

3) двойные R − C или R – L цепочки

Рисунок 3.4.9 Пример апериодического звена 2-го порядка

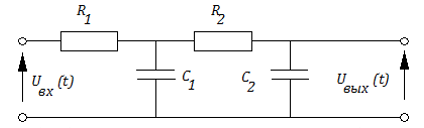
Если звено представлено в переменных состояния в матричной форме таким образом:

то звено будет апериодическим 2-го порядка, если:

Видео:Теория автоматического управления. Лекция 7. Типовые звенья САУСкачать

Пример

В качестве примера возьмём модель демпфера, которую мы уже использовали в лекциях. (см. Рисунок 3.4.10) Структурная схема модели описывает уравнения динамики, описанные в начале статьи. Свойства системы заданы в списке общих сигналов проекта (см. рис. 3.4.11). Для получения из демпфера апериодического звена 2-го порядка необходимо увеличить силу трения таким образом, чтобы (как показано выше) коэффициент T₁ был больше, чем 2 х T₂. В этом случае D>0 и из колебательного звена мы получим апериодическое 2-го порядка.

Рисунок 3.4.10 Структурная схема модели демпфера. Рисунок 3.4.11 Параметры модели

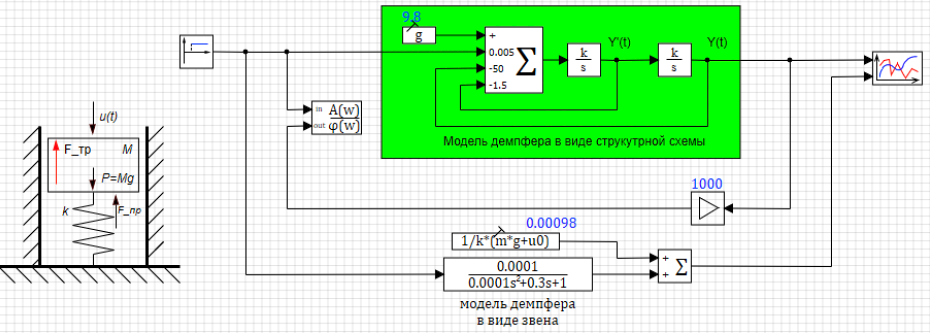
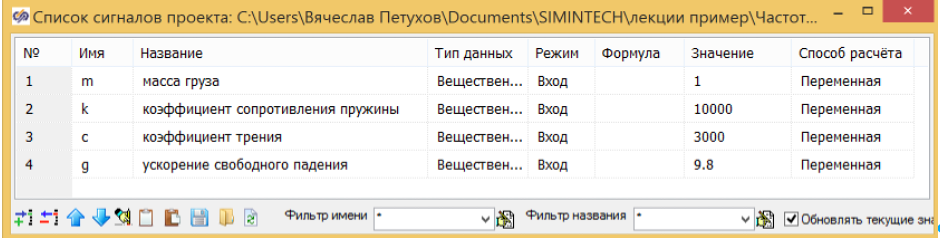
Для дальнейшего исследования на схему добавлена модель демпфера в виде звена общего вида, а его свойства заданы в виде формул, выражающих коэффициенты звена через параметры модели. (см. рис. 3.4.12).

Рисунок 3.4.12. Параметры для модели демпфера в виде звена

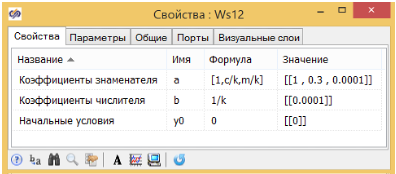
Выполним моделирование переходного процесса при ступенчатом изменении приложенной силы и сравним переходные процессы в двух вариантах модели демпфера. График переходного процесса (см. рис. 3.4.13) показывает, что переходные процессы в двух моделях полностью идентичны:

Рисунок 3.4.13 Переходные процессы в двух моделях.

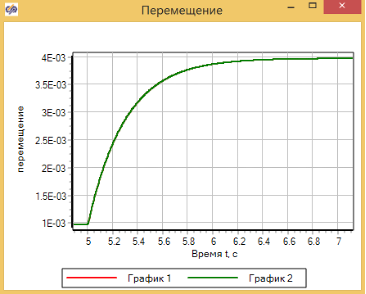
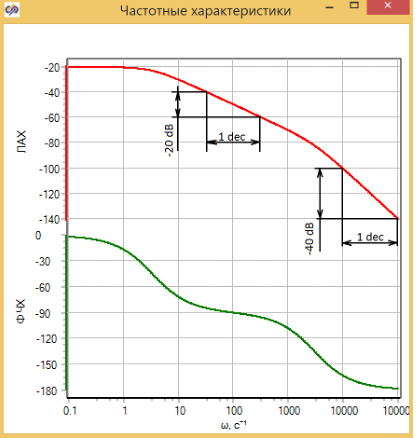
График частотных характеристик звена (ЛАХ и ФЧХ) представлен на рисунке 3.4.14 На графике видно две точки излома характеристики ЛАХ в которых наклон последовательно меняется с 0, до 20дБ/дек и с 20дБ/дек до 40 дБ/дек.

Рисунок 3.4.14 Частотные характеристика ЛАХ и ФЧХ

Для демонстрации влияния изменения Т₁ на свойства звена выполним моделирование, в котором структурная схема является эталонной, а в модели звена будем уменьшать коэффициент силы трения (коэффициент T₁).

Источником воздействия будет меандр, с периодом 3 секунды.

Для изменения свойств звена создадим блок на языке программирования. Данный блок, в процессе моделирования, постепенно уменьшает коэффициент Т₁ для модели в виде звена. Этот же блок готовит данные для отображения на 3D графике переходного процесса.

Общая схема модели приведена на рисунке 3.4.15.

Рисунок 3.4.15 Схема демпфера с изменения свойств блока

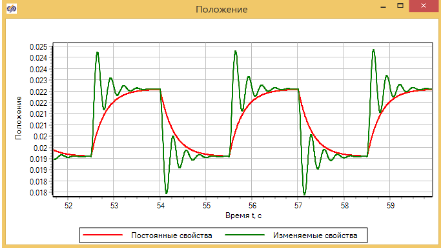
Меандр задает изменение приложенной силы 0 – 30 Н (входного воздействия) с полупериодом 1.5 сек. График изменения положения приведен на рисунке 3.4.16 Видно, что на первом изменении графики совпадают, но потом по мере накопления отличий в параметрах динамика изменения положения начинает меняться.

Рисунок 3.4.16 Графики положения демпферов.

Первая часть процесса изображена на рисунке 3.4.17 Видно, что снижение силы трения обеспечивает более быстрое изменении положения демпфера.

Рисунок 3.4.17 Начальная часть графика

Конечная часть графика представлена на рисунке 3.4.19. Дальнейшее снижение силы трения приводит к тому, что процесс перехода при ступенчатом изменении воздействия становится колебательным.

Рисунок 3.4.18 Конечная часть моделировани

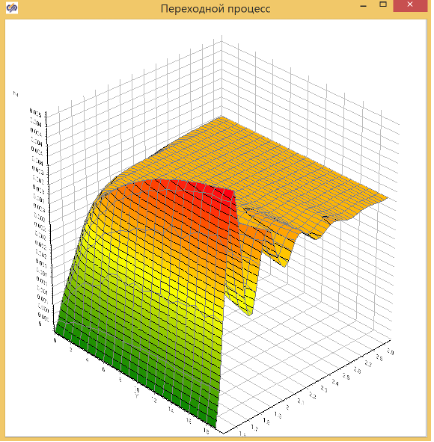
ЗD поверхность отображает переходный процесс при ступенчатом увеличении воздействия в блоке меандр. По оси Z отражается положение демпфера, по оси Y – время после увеличения входного воздействия в блоки меандр, по оси X – изменений T₁ (уменьшение силы трения).

Рисунок 3.4.19 Поверхность переходного процесса при снижении трения

В заключение, сравним переходные процессы для разных параметров T₁ (разных коэффициентов трения). Поскольку все основные блоки в SimInTech являются векторными, создадим модели 7-ми демпферов из одного звена. Для этого в главном окне программы подготовим 7 векторов значений с разными коэффициентами трения. Скрипт приведен на рисунке 3.4.20.

Рисунок 3.4.20 Скрипт модели для задания параметров 7 демпферов

Четвертый вектор содержит переходное значение T₁. Как было показано выше, переходное значение T₁, при котором апериодическое звено второго порядка превращается в колебательное рассчитывается по формуле T₁ = 2хT_2.

В модели, в свойствах блока указываем эти векторы в столбце «формулы», и теперь блок может рассчитывать одновременно 7 демпферов одним блоком. (см. рис. 3.4.21)

Рисунок 3.4.21 Настройка параметров блока для векторного расчета

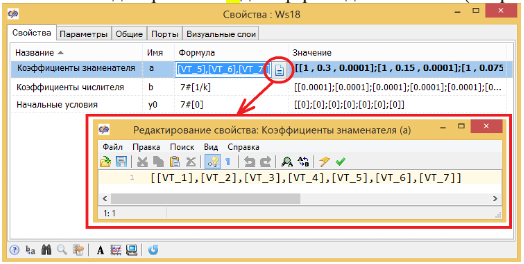
Общая схема модели в этом случае будет выглядеть как показано на рисунке 3.4.22 Ступенчатое изменение силы передается в блок «Размножитель», где преобразуется в вектор из 7 воздействий. Данный вектор передается в блок, где и происходит расчёт семи вариантов демпфера.

Рисунок 3.4.22 Схема модели 7-и демпферов

Результат переходного процесса представлен на рисунке 3.4.23. Видно, что 3 демпфера ведут себя как апериодическое звено второго порядка, 3 демпфера явно превратились в колебательные.

Рисунок 3.4.23 Перемещение 7 демпферов при ступенчатом воздействии

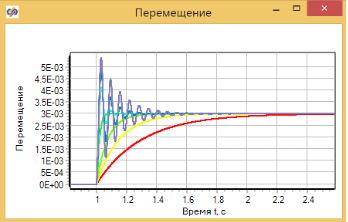
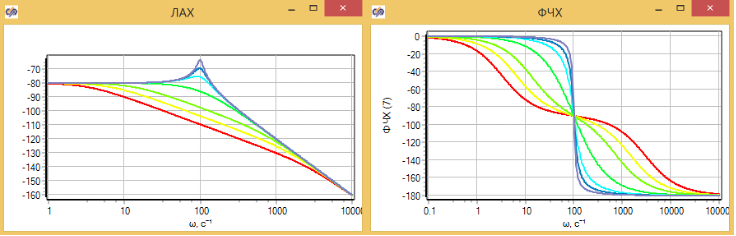
Характеристики ЛАХ и ФХЧ представлены на рисунке 3.4.24. Наглядно видно, как постепенно, при снижении коэффициента трения исчезают два излома на графике ЛАХ, и звено превращается в колебательное, о котором будем говорить в следующей части.

Рисунок 3.4.25 Частотные характеристики 7-и демпферов

Модели с примерами для самостоятельного изучения можно взять по ссылке.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Апериодическое звено второго порядка

Оно описывается тем же дифференциальным уравнением, что и колебательное звено, но при условии Т₀ > 2 T . Корни характеристического уравнения становятся действительными, звено перестает быть колебательным и превращается в апериодическое.

.

При отсутствии изменения выходной величины ( p = 0) K ( p ) = k , коэффициенту усиления.

Комплексная частотная характеристика

.

Действительная и мнимая частотные характеристики

,

.

Последнее выражение показывает, что амплитудная частотная характеристика резко отличается от таковой для колебательного звена. При w = 0 значение амплитуды равно k . С увеличением

Рис. Амплитудная частотная характеристика

апериодического звена второго порядка

частоты амплитуда уменьшается до нуля. То есть, это монотонная кривая.

Аналогично колебательному звену, фазовая частотная характеристика в интервале 0 £ w £ 1 / T рассчитывается по формуле

В интервале 1 / T w ¥ используется формула

Для апериодического звена асимптотическая логарифмическая амплитудная частотная характеристика получается такой же, как на рисунке.

Переходная функция получается решением уравнения (3.7) при условии x = 1,

и начальных условиях h = 0, dh/ dt = 0 при t = 0.

имеет действительные корни

.

Они действительные и отрицательные так как в силу условия апериодичности звена T ₀ > 2 T .

Переходная функция получается в виде:

.

При t = 0 h ( t ) = 0. С увеличением t кривая монотонно стремится к пределу h = k .

Апериодическое звено второго порядка можно назвать типовым условно, потому что такая же математическая модель реализуется двумя инерционными звеньями, соединенными последовательно.

Рис. Два последовательно соединенных инерционных звена

Чтобы показать это достаточно, исходя из дифференциальных уравнений звеньев А и Б, получить дифференциальное уравнение.

Пусть уравнения звеньев имеют вид

А) ,

Б) .

Выделим из уравнения звена Б x ₁ , продифференцируем по t и заменим соответствующие величины в уравнении А. Это приводит к выражению

где x , y — входная и выходная величина системы из двух инерционных звеньев.

.

Видео:10) ТАУ для чайников Части 4.1. и 4.2. Типовые динамические звенья. Усилитель. Апериодическое звено.Скачать

Апериодическое (инерционное, статическое) звено. Передаточная функция и уравнения

Дифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде:

Где: k – коэффициент передачи, Т₀ – постоянная времени.

Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции.

Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена).

Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Х_вых(р) и Х_вх(р) функций вещественных переменных Х_вых(τ) и Х_вх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа:

Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены:

Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена.

Оригинал дифференциального уравнения апериодического звена имеет следующий вид:

Операторная форма записи (изображения) уравнения апериодического звена:

Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ).

Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом:

Из полученного выражения достаточно легко выделить отношение Х_вых(р) / Х_вх(р), которое называется передаточной функцией и для апериодического звена имеет вид:

У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ).

На практике чаще всего используется АФЧХ или АФХ.

Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент).

Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α:

После использования формулы Эйлера:

Где |W| — длина вектора или вектор по модулю, i – мнимое число:

Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний.

Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид:

Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования:

Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k.

На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т₀ в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т₀ и k в передаточной функции звена.

Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак).

В бак поступает определенное количество воды с расходом Q₁. В то же время из бака вытекает вода с расходом Q₂. Регулируемый параметр в этой системе Х_вых – уровень воды в баке H.

При подаче единичного скачка Q₁ (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q₂. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k.

В литературе объекты с передаточной функцией апериодического звена называют статическими.

🔥 Видео

11)ТАУ для чайников. Часть 4.3. Колебательное звеноСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Дифференциальное уравнение от Бермана ★ Решите дифференциальное уравнение 2-го порядка ★ xy''=y'Скачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами МЕТОДОМ ЛАПЛАСАСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Лекция №3. Апериодическое звено. Прокопенко В. А.Скачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать