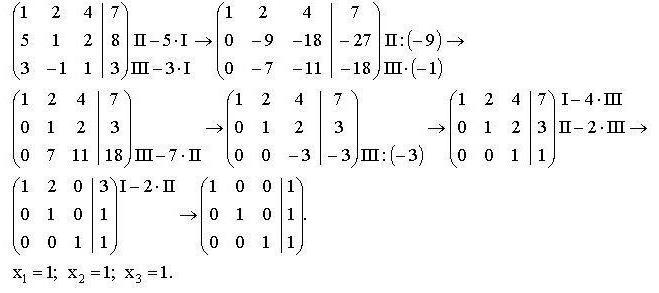Аналитические методы решения систем уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ И ИХ СИСТЕМ В ПАКЕТАХ СИМВОЛЬНОЙ МАТЕМАТИКИ

Автор работы _____________________________________И. Ю. Добрынькина

Направление подготовки 44.03.05 Педагогическое образование

Профиль Информатика. Математика

Руководитель работы_______________________________ Т. В. Кормилицына

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Введение

Одним из факторов, определяющих уровень развития современного общества и его интеллектуальные возможности, является оснащенность его средствами вычислительной техники. Сфера использования ЭВМ в настоящее время настолько широка, что нет такой области, где ее применение было бы нецелесообразным.

Развитие вычислительной техники повлекло за собой создание и совершенствование языков программирования, а вследствие этого и программного обеспечения. Однако совершенствование программного обеспечения связано с увеличением его сложности. Поэтому процесс разработки программ становится трудоемким, а их модификация и сопровождение затруднительным.

Традиционная инженерная деятельность связана с решением совокупности разнообразных задач расчета, проведением экспериментов, оформление документации. Развитие современных методов и компьютерной технологии существенно изменяет деятельность специалиста.

В начале 90-х гг. на смену универсальным языкам программирования пришли специализированные системы компьютерной математики (СКМ). Среди них наибольшую известность получили системы Eureka, Mercury, Mathcad, Derive, Mathematica 2/3/4, Maple V R3/R4/R5 и Maple 6 и др.

Научное программное обеспечение и математические пакеты играют важную роль в современном естествознании и технике. Такие пакеты как Axiom, Derive, Maсsyma, Maple, MatLab, MathCAD, Mathematica широко распространились в университетах, исследовательских центрах и компаниях развитых стран. Владение одним или несколькими математическими пакетами и регулярное использование их в работе будь то исследовательская или преподавательская задача быстро становится нормой для специалиста.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

1. Mathematica . Решение простейших дифференциальных уравнений

Для решения дифференциальных уравнений в аналитической форме в пакете Mathematica используется функция DSolve, дифференциальное уравнение 29 относительно функции y(x). Функция y и все ее производные должны быть записаны с аргументом, заключенным в квадратные скобки: y[x], y’[x]

Функция DSolve стремится найти общее решение ДУ в явном виде и выдает результат в виде списка правил замены, причем каждое решение заключается в фигурные скобки. Для ДУ порядка n общее решение содержит n произвольных констант, которые обозначаются C[1], C[2],…,C[n]. Для получения частного решения необходимо в качестве первого аргумента DSolve указать список, состоящий из самого уравнения и начальных или граничных условий:

Найденные с помощью DSolve решения можно подставить в любое выражение, содержащее y(x). Однако это решение не определяет правил замены производных y’(x), y’’(x) и так далее, например:

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Чтобы получить решение, не имеющее этого недостатка, нужно в качестве второго аргумента функции DSolve записать только имя искомой функции, не указывая ее аргумент. В этом случае решение представляется в виде чистой функции («purefunction»-объекта), в котором роль аргумента x, в некоторых случаях, играет символ «#1», а признаком этого объекта является символ «&». Полученное решение можно подставить в любое выражение, содержащее как функцию y(x), так и ее производные:

Для решения систем уравнений в качестве первого аргумента функции указывается список уравнений, а в качестве второго аргумента – список искомых функций:

Если в список уравнений включить необходимое количество начальных или граничных условий, то будет найдено частное решение системы ДУ, не содержащее произвольных постоянных:

Для некоторых уравнений решение может быть выражено через спецфункции, встроенные в пакет Mathematica. Если же DSolve не может найти аналитического решения ДУ, то Mathematica просто перепечатывает введенные данные в выходную ячейку:

В этом случае нужно преобразовать ДУ к более простому виду, используя правила, известные из теории дифференциальных уравнений. Если же аналитически решить уравнение не удается, можно попробовать решить его численно.

Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

1.2 Примеры из математического анализа

Разумеется, роль систем символьной математики далеко не исчерпывается приведенными выше примерами. Эти системы способны преобразовывать сложнейшие алгебраические выражения, находить аналитические решения сложных систем линейных, нелинейных и дифференциальных уравнений, манипулировать со степенными многочленами, вычислять производные и интегралы, анализировать функции, находить их пределы и т. д. Это видно уже из примеров, представленных на рис. 1.6 .

В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate — интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).

Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:

Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.

DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], х]

DSolve [у» [х] — у’ [х] — 6 у [х] == 0, у [х] , х] <| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]>>

DSolve [у» [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]

DSolve[y'[x] == Sin[Ex] , y[x] , x]

DSolvefz2 w»[z] +zw'[z] — (z2 + l)w[z] ==0, w[z], z]

<BesselI[l, z] C[l] +BesselK[l, z] C[2] >>

Как нетрудно заметить, аналитические решения дифференциальных уравнений могут содержать не только элементарные, но и специальные математические функции, что заметно расширяет возможности применения системы Mathematica в решении задач динамического моделирования.

Видео:Решение систем уравнений методом подстановкиСкачать

1. 3 Аналитическое решение дифференциальных уравнений

Общее решение дифференциальных уравнений.

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options),где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y»+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).

Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).

eq:=: > s:=solve(eq,); s:= Для нахождения частного решения следует выполнить подстановку конкретного значения одной из переменных при помощи команды subs: > subs(,s); «>

Видео:Матричный метод решения систем уравненийСкачать

2. Аналитические вычисления в Mathcad

С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, вычисляют в производные и неопределенные интегралы, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить результат в виде некоторой функции. В программе Mathcad при проведении символьных преобразований конкретные значения, присвоенные переменным, игнорируются – переменные рассматриваются как неопределенные параметры.

Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и продублированы на аналогичной панели инструментов.

Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).

В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в выражении. Например, команда Solve (Решить) ищет корни функции, заданной данным выражением. В примере в аналитической форме получены все корни полинома второй степени: сначала применена команда solve для решения, а затем simplify для упрощения результата:

Другие возможности использования этого меню включают:

аналитическое дифференцирование и интегрирование: Символика > Переменная > Дифференцировать (Symbolics > Variable > Differentiate) и Символика > Переменная > Интегрировать (Symbolics > Variable > Integrate);

замена переменной: Символика > Переменная > Подставить (Symbolics > Variable > Substitute) – вместо переменной подставляется содержимое буфера обмена;

Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравния и неравенства, а последняя формула блока должна выглядеть как

где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:

Отметим, что функция Find пытается найти решение в аналитической форме. В том случае, если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.

Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.

Любое аналитическое вычисление можно применить с помощью ключевого слова. Cписок ключевых слов

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

3. Решение систем дифференциальных уравнений в символьном виде в системе MATLAB

Для решения дифференциальных уравнений в форме Коши MatLAB имеет функцию dsolve(‘eqn1’,’eqn2’, …), которая возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqni(вначале задаются уравнения, затем начальные условия).

По умолчанию независимой переменной считается ‘t’ . Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d^2/dt^2 и т.д.

Начальные условия задаются в виде равенств ‘y(a) = b’ или ‘Dy(a) = b’, где y — независимая переменная, a и b – константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решений будут присутствовать произвольные постоянные С1, С2 и т.д. Вывод осуществляется в виде массива записей.

Обратите внимание, что уравнение, которое требуется решить, задано как строка, то есть взято в одинарные кавычки. Ответ представляет собой точное (символьное) решение 1+корень(5). Для получения числовых решений введите double (ans) или vpa (ans), чтобы отобразить больше знаков. Ввод с командой solve может также быть символьным выражением, но в этом случае программа MATLAB потребует, чтобы правая часть выражения была заключена в скобки, и фактически синтаксис решения уравнения х 2 — Зх = -7 будет выглядеть так:

Ответ представляет собой точное (символьное) решение (3 + корень(19i))/2 (сложные числа, где буква i в ответе ставится для мнимой единицы V-1). Для получения числовых решений введите double (ans) или vpa (ans), чтобы отобразить больше знаков.

Видео:Решение систем уравнений методом сложенияСкачать

Заключение

В настоящее время научное программирование претерпевает серьезную трансформацию: развиваются интегрированные среды, основанные на алгоритмических языках, и растет применение универсальных математических систем (Maple, Mathematica, MATLAB, MatCad и др.). Эти системы имеют дружественный интерфейс, реализуют множество стандартных и специальных математических операций, снабжены мощными графическими средствами и обладают собственными языками программирования. Все это предоставляет широкие возможности для эффективной работы специалистов разных профилей, о чем говорит активное применение математических пакетов в научных исследованиях и в преподавании. С помощью этих пакетов проще готовить и выполнять задания, устраивать демонстрации и гораздо быстрее решать исследовательские и инженерные задачи.

Конечным продуктом исследования выступают публикации, подготовка, распространение и использование которых в настоящее время требует квалифицированного применения компьютера. Это касается редактирования текста, изготовления графических материалов, ведения библиографии, размещения электронных версий в Интернет, поиска статей и их просмотра. Де-факто сейчас стандартными системами подготовки научно-технических публикаций являются различные реализации пакета TeX и текстовый редактор Word. Кроме того, необходимы минимальные знания о стандартных форматах файлов, конверторах, программах и утилитах, используемых при подготовке публикаций.

Математические пакеты Maple и MATLAB — интеллектуальные лидеры в своих классах и образцы, определяющие развитие компьютерной математики. Компьютерная алгебра Maple вошла составной частью в ряд современных пакетов, численный анализ от MATLAB и наборы инструментов (Toolboxes) уникальны. Сами пакеты постоянно совершенствуются, развивая аппарат и пополняя ресурсы. Пакет Maple и вычислительная среда MATLAB — мощные и хорошо организованные системы, надежные и простые в работе. Освоение даже части их возможностей даст несомненный эффект, а по мере накопления опыта придет настоящая эффективность от взаимодействия с ними.

В заключение, отметим, что пользователь пакетов компьютерной математики должен иметь представление об основных численных методах. Вообще говоря, появление современных вычислительных систем значительно облегчает доступ к компьютеру непрофессионалам в области программирования, и поддерживает постоянное стремление к их усовершенствованию и освоению новых компьютерных технологий.

Видео:6 способов в одном видеоСкачать

Список литературы

1. Дьяконов В.П. Справочник по применению системы PC MATLAB. — М.: «Физматлит» , 1993. — С. 112. — ISBN 5-02-015101-7

2. Дьяконов В.П. Компьютерная математика. Теория и практика. — СПб: «Питер» , 1999, 2001. — С. 1296. — ISBN 5-89251-065-4

3. Дьяконов В.П. MATLAB 5 — система символьной математики. — М.: «Нолидж» , 1999. — С. 640. — ISBN 5-89251-069-7

4. Дьяконов В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений. Специальный справочник. — СПб.: «Питер» , 2002. — С. 608. — ISBN 5-318-00667-608

5. Дьяконов В.П., Круглов В.В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. — СПб.: «Питер» , 2002. — С. 448. — ISBN 5-318-00359-1

6. Дьяконов В. П. Simulink 4. Специальный справочник. — СПб.: «Питер» , 2002. — С. 528. — ISBN 5-318-00551-9

7. Дьяконов В . П . MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2002. — С. 768. — ISBN 5-98003-007-7

8. Дьяконов В.П. MATLAB 6/6.1/6.5 + Simulink 4/5 в математике и моделировании. Основы применения. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2003. — С. 576. — ISBN 5-93455-177-9

9. Дьяконов В . П . MATLAB 6.0/6.1/6.5/6.5+SP1 + Simulink 4/5. Обработка сигналов и изображений. Полное руководство пользователя. — Москва.: «СОЛОН-Пресс» , 2005. — С. 592. — ISBN 5-93003-158-8

10. Дьяконов В . П . MATLAB 6.5/7.0 + Simulink 5/6. Основы применения. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 800. — ISBN 5-98003-181-2

11. Дьяконов В.П. MATLAB 6.5/7.0 + Simulink 5/6 в математике и моделировании. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 576. — ISBN 5-98003-209-6

12. Дьяконов В . П . MATLAB 6.5/7.0 + Simulink 5/6. Обработка сигналов и проектирование фильтров. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 576. — ISBN 5-98003-206-1

13. Дьяконов В . П . MATLAB 6.5/7.0/7 SP1 + Simulink 5/6. Работа с изображениями и видеопотоками. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 400. — ISBN 5-98003-205-3

14. Дьяконов В . П . MATLAB 6.5/7.0/7 SP1/7 SP2 + Simulink 5/6. Инструменты искусственного интеллекта и биоинформатики. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2005. — С. 456. — ISBN 5-98003-255-X

15. Дьяконов В . П . MATLAB R2006/2007/2008 + Simulink 5/6/7. Основы применения. Изд-е 2-е, переработанное и дополненное. Библиотека профессионала. — Москва.: «СОЛОН-Пресс» , 2008. — С. 800. — ISBN 978-5-91359-042-8

16. Дьяконов В.П. MATLAB 7.*/R2006/2007. Самоучитель. — Москва: «ДМК-Пресс» , 2008. — С. 768. — ISBN 978-5-94074-424-5

17. Дьяконов В.П. SIMULINK 5/6/7. Самоучитель. — Москва: «ДМК-Пресс» , 2008. — С. 784. — ISBN 978-5-94074-423-8

18. Дьяконов В.П. Вейвлеты. От теории к практике. Полное руководство пользователя. Изд-е 2-е переработанное и дополненное. — Москва: «СОЛОН-Пресс» , 2004. — С. 400. — ISBN 5-98003-171-5

19. Чарльз Генри Эдвардс, Дэвид Э. Пенни Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3- е изд . — М .: « Вильямс » , 2007. — ISBN 978-5-8459-1166-7

20. Алексеев Е.Р., Чеснокова О.В MATLAB 7. Самоучитель.. — Пресс , 2005. — С. 464.

21. Курбатова Екатерина Анатольевна MATLAB 7. Самоучитель. — М.: «Диалектика» , 2005. — С. 256. — ISBN 5-8459-0904-X

22. Джон Г. Мэтьюз, Куртис Д. Финк Численные методы. Использование MATLAB = Numerical Methods: Using MATLAB. — 3- е изд . — М .: « Вильямс » , 2001. — С . 720. — ISBN 0-13-270042-5 u

Видео:графический и аналитический способы решения систем линейных уравнений с двумя неизвестнымиСкачать

Примеры систем линейных уравнений: метод решения

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Видео:Методы решения систем уравнений. Видеоурок по алгебре 9 классСкачать

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.

Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Видео:Решение системы уравнений методом ГауссаСкачать

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

1. Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
2. Почленно сложить полученное выражение и найти одно из неизвестных.
3. Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Видео:Алгебра 9 класс. Графическое решение систем уравненийСкачать

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.

Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.

Решение для полученных в итоге системы находят методом сложения.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Наглядный метод решения систем

Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.

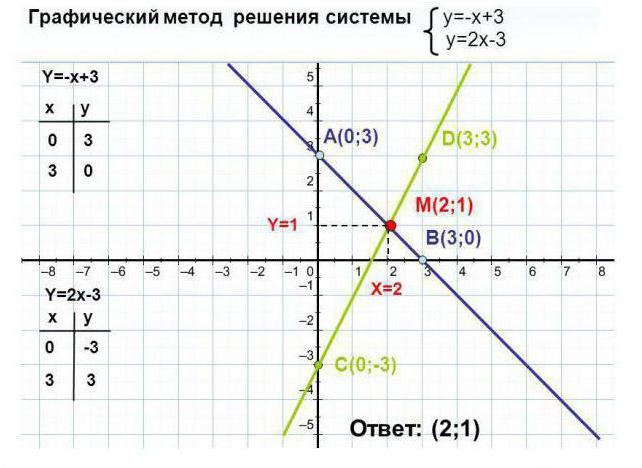
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.

Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.

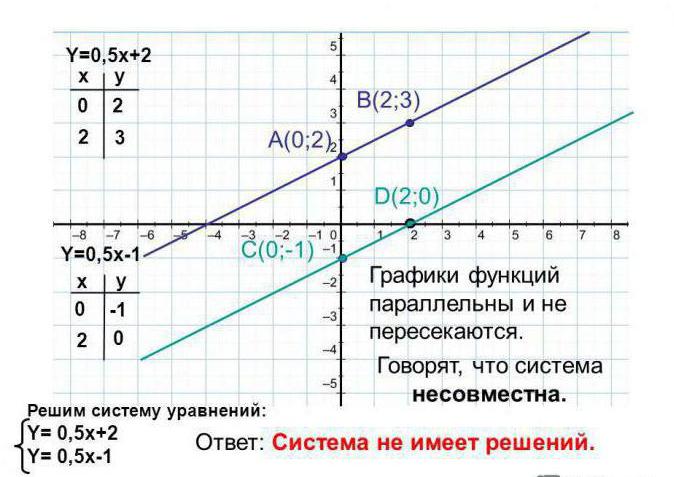
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

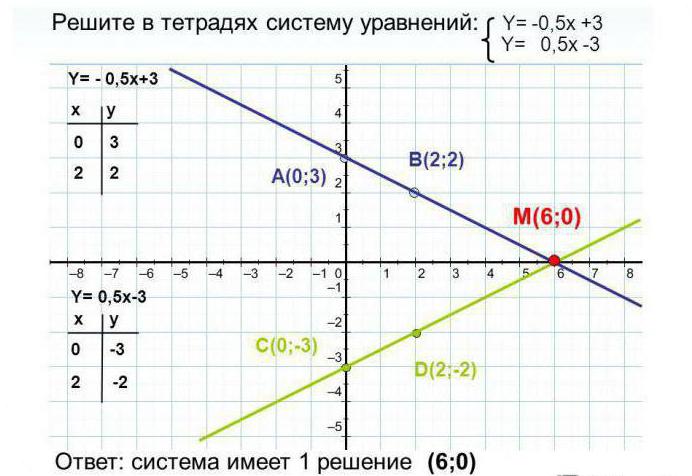
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.

Видео:Аналитические методы решения систем рациональных уравненийСкачать

Матрица и ее разновидности

Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. Матрица вида n*m имеет n — строк и m — столбцов.

Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.

Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.

Видео:Решение систем уравнений методом сложенияСкачать

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a₁b₂c₃ + a₁b₃c₂ + a₃b₁c_{2 +} a₂b₃c₁ + a₂b₁c₃ + a₃b₂c₁. Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Решение примеров систем линейных уравнений матричным методом

Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a_nm — коэффициенты уравнений, матрица — вектор x_n — переменные, а b_n — свободные члены.

Далее необходимо найти обратную матрицу и умножить на нее исходную. Найти значения переменных в полученной единичной матрицы легко выполнимая задача.

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x₃-2x₄=11 и 3x₃+2x₄=7. Решение любого из уравнений позволит узнать одну из переменных x_n.

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. Вертикальная черта отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

Решение уравнений

Цель лекции. Показать технику численного решения нелинейных уравнений с использованием сервисов MathCAD. Показать различные методы аналитического решения систем линейных уравнений.

4.1. Численное решение нелинейных уравнений

Относительно небольшое количество задач решения уравнений можно решить аналитически. Аналитическое решение предполагает точное определение корней либо нахождение алгоритма, по которому корни всегда могут быть найдены. На практике часто приходится искать решение при помощи численных методов [1, 11]. Уравнения решаются численными методами с заданной погрешностью. В MathCAD погрешность задается системной константой TOL . Как правило, отыскание корней алгебраического уравнения (или системы уравнений) численными методами связано с двумя задачами:

• локализация корней, т. е. определение их существования в принципе, а также исследование их количества и примерного расположения;
• собственно отыскание корней с заданной погрешностью

Для численного решения уравнений в MathCAD существуют встроенные функции[1, 10], в которых реализованы алгоритмы известных численных методов: итерационный метод секущих ; различные градиентные методы и другие. Почти все встроенные функции предполагают, что корни уже приблизительно локализованы.

Использование функции root()

Рассмотрим решение простейших уравнений вида F(x)=0 . Решить уравнение – значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Если функция нескольких аргументов F(x, у, ..)=0. , все остальные значения должны быть заданы для искомого x . Для локализации корней (исследования их количества и примерного расположения) полезно построить график функции и определить все точки пересечения графика функции с осью OX.

Функция root () вычисляет значение переменной, при котором F(x, у, ..)=0 . Если уравнение имеет несколько корней, функцию надо вызывать соответствующее число раз. Вычисления реализуются итерационным методом. Данный метод заключается в постепенном приближении к искомому корню с некоторой точностью от начального значения переменной. Точность вычислений задаётся системной переменной TOL , определённой в меню Tools/ Worksheet Options .. По умолчанию равной 0.001.

root(F(x, у, . ), x, [a, b]) возвращает с заданной точностью значение переменной, x , лежащей между a и b при котором функция равна нулю. Значения F() для a и b должны быть разных знаков. Третий аргумент не обязателен. Выбор решения определяется выбором начального значения переменной

Пример 4.1

Решить уравнение