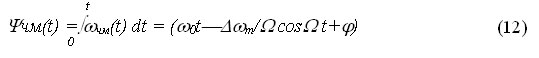Амплитудная модуляция временная диаграмма и уравнение

Видео:Амплитудная модуляцияСкачать

Изучение темы «Амплитудная модуляция» по дисциплине СПО «Теория электросвязи»

Для студентов 2 курса специальности 11.02.09 Многоканальные телекоммуникационные системы и 11.02.11 Сети связи и системы коммутации. Содержит лекционный материал и методические указания к выполнению практической работы.

Просмотр содержимого документа
«Изучение темы «Амплитудная модуляция» по дисциплине СПО «Теория электросвязи»»

Тема лекции: Амплитудная модуляция

План лекции: 1. Определение процессов модуляции и детектирования (демодуляции). 2. Временная диаграмма и математическая модель АМ-сигнала. 3. Спектр АМ -сигнала.
1. Определение процессов модуляции и детектирования (демодуляции).

Модуляция – это процесс изменения одного или нескольких параметров несущей высокочастотные колебания в соответствии с изменением параметров сигнала, воздействующего на него (модулирующего сигнала).

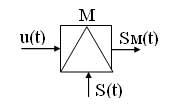
Параметры несущей, изменяющиеся во времени под воздействием модулирующего сигнала, называются информационными, так как в их изменениях заложена передаваемая информация. Физический процесс управления параметрами несущей и является модуляцией. Таким образом, любой модулятор 1 (рис. 1) должен иметь два входа: один – для несущей, другой – для модулирующего сигнала. Модулированный (высокочастотный) сигнал на выходе модулятора зависит от времени и от модулирующего сигнала U_M(t), поэтому и обозначается как функция двух аргументов U_AM (U_M, t).

Модулированные сигналы различаются по виду несущей и по модулируемым параметрам. В качестве несущей в настоящее время широко используются высокочастотные гармонические колебания, периодическая последовательность импульсов, реже – колебания специальной формы.

Гармоническая несущая U_H(t)=U_mН cos(ωt + φ), например, характеризуется тремя свободными параметрами: амплитудой, частотой и фазой. Все они могут быть информационными. Изменяя один из них при постоянстве других, получаем три основных вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ).

Модулированный сигнал при гармонической несущей в общем случае можно представить в виде:

За интервал времени, в течение которого полная фаза ωt изменится на 2π, огибающая не успеет сильно измениться и ее можно считать медленно меняющейся.

Рис. 1. Модулятор

Главная особенность любой модуляции – преобразование спектра модулирующего сигнала. В общем случае происходит расширение спектра, а при гармонической несущей – перенос спектра в область около частоты несущей. Именно это обстоятельство и привело к использованию только модулированных сигналов в радиосвязи и многоканальной связи.

Модулятором называют устройство, предназначенное для получения модулированного сигнала.

2. Временная диаграмма и математическая модель АМ-сигнала.

Амплитудная модуляция – это процесс изменения амплитуды несущего высокочастотного колебания в соответствии с законом изменения мгновенных значений модулирующего низкочастотного сигнала.

Пусть модулирующий сигнал U_M (см. рис. 2а) является гармоническим колебанием с частотой F, амплитудой U_mM и начальной фазой, равной нулю.

В качестве несущего колебания в электросвязи обычно используют также гармонические колебания U_H (см. рис. 2б) с амплитудой U_MH, высокой частотой fн. На рис. 2в показана временная диаграмма АМ сигнала, полученная на основании определения АМ. На временном интервале от 0 до t, пока U_M=0 (модулирующий сигнал отсутствует), отсутствует причина, вызывающая изменение амплитуды несущих колебаний, и АМ сигнал повторяет несущие колебания. В момент времени t₁ появляется модулирующий сигнал,

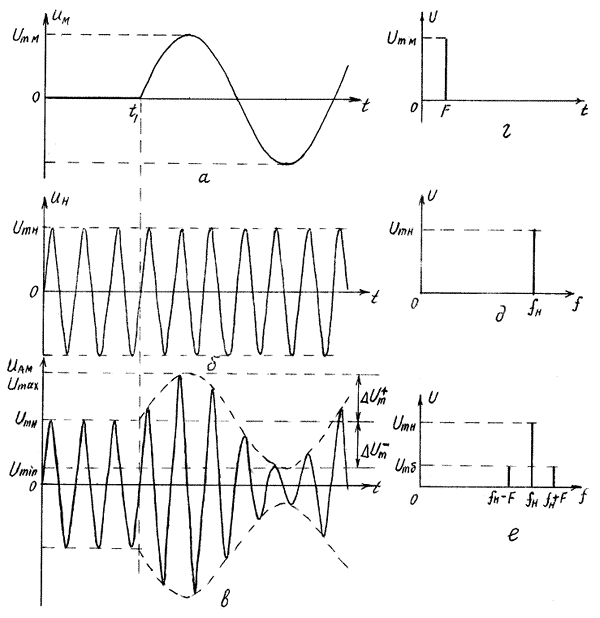
Рис. 2. Временные и спектральные диаграммы АМ-сигнала

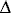
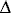
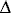
амплитуда несущих колебаний начинает возрастать пропорционально мгновенным значениям модулирующего сигнала U_M. Максимальному значению U_mM модулирующего сигнала U_M соответствует приращение амплитуды АМ сигнала U_M + относительно U_MH. Минимальному значению –U_MH модулирующего сигнала U_M соответствует приращение амплитуды АМ U_M + и U_M — должен быть равны: U_M + = U_M — = U_M. Интенсивность процесса АМ (глубина модуляции) определяется коэффициентом амплитудной модуляции m. Коэффициент амплитудной модуляции равен U_M/ U_MH

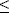
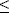
Коэффициент амплитудной модуляции может изменяться в пределах 0 m 1, иногда он выражается в процентах: m%=m·100%.

Если гармонические колебания с амплитудой U_MH и частотой f_H модулировать по амплитуде гармоническим сигналом с амплитудой U_mM и частотой F, то в результате получаются гармоническое колебание U_AM, которое можно рассматривать сумму следующих трех гармонических колебаний: U_H с амплитудой U_MH и частотой f_H, с амплитудой mU_MH/2 и частотой f_H-F и с амплитудой mU_MH/2 и частотой f_H-F.

Спектр АМ сигнала

Спектр амплитуд АМ сигнала при гармоническом модулирующем сигнале представлен на рис. 2.е Согласно рис. 2.е спектр АМ сигнала является линейным (дискретным) с тремя спектральными линиями: центральная из них является спектральной линией несущего колебания с амплитудой U_MH и частотой f_H, а две другие – боковые с амплитудой U_Mб=mU_MH/2. Боковые колебания с частотой f_H – F называют нижней боковой, а с частотой f_H + F называют верхней боковой. Амплитуды боковых колебаний одинаковы и даже при m=1 не превышают половины несущего колебания U_MH

Согласно рис. 2.е ширина спектра АМ сигнала при гармоническом модулирующем сигнале равна

f_AM=f_MAX – f_MIN= (f_H + F) – (f_H – F)=2F (1.2)

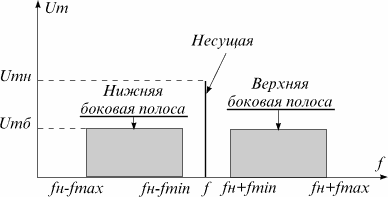
Спектр АМ сигнала при сложном модулирующем сигнале качественно определяется из следующих рассуждений. Допустим, что спектр сложного модулирующего сигнала сплошной и ограничен частотами F_MIN и F_MAX. Каждая частота этого спектра образует боковые составляющие с частотами f_H±F. Таким образом, в спектре сложномодулированного АМ сигнала, помимо несущего колебания с частотой f_H, содержатся группы верхних и нижних боковых колебаний, образующих соответственно верхнюю боковую полосу от f_H + F_MIN до f_H + F_MAX и нижнюю боковую полосу частот от f_H — F_MAX до f_H — F_MIN АМ сигнала (см. рис. 3).

Рис 3. Спектр сложно модулированного АМ сигнала.

Согласно рис. 3 ширина спектра сложно модулированного АМ сигнала равна

f_AM=f_MAX – f_MIN= (f_H + F) – (f_H – F)=2F (1.3)

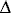
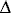
Из уравнения (1.3) следует, что ширина спектра сложно модулированного АМ сигнала f_AM равна удвоенному значению максимальной частоты f_MAX спектра модулирующего низкочастотного сигнала, f_AM=2F_MAX.

Энергетический анализ АМ сигнала показывает, что при 100%-ной глубине модуляции гармоническим сигналом (m=1) 66,7% мощности приходится на несущие колебания, не содержащие информации, а доля мощности обоих боковых колебаний, содержащих информацию составляет всего 33,3%. При сложном модулирующем сигнале эта доля еще уменьшается, хотя все информация в передаваемом сообщении заключается именно в боковых составляющих.

Для более эффективного использования мощности АМ сигнала используются неполночастотные АМ сигналы:

АМ сигнал, состоящий из двух боковых полос без несущей. При этом каждая боковая полоса содержит одну и ту же информацию. Ширина передаваемого спектра такая же, как и полночастотного АМ сигнала (см. рис. 4.б).

АМ сигнал, состоящий из одной боковой полосы (любой), без другой боковой полосы и без несущей. (см. рис. 4.в).

Рис. 4. Спектральные диаграммы АМ сигналов:
а — полночастотный АМ сигнал;
б — АМ сигнал из двух боковых полос без несущей;
в — АМ сигнал из одной нижней боковой полосы.

Передача одной боковой полосы обладает следующими преимуществами:

не тратится мощность на передачу несущих колебаний; за счет этого можно увеличить мощность колебаний передаваемой боковой полосы, и дальность действия связи;

при отсутствии модуляции мощность не расходуется, так как передачи несущих колебаний нет;

меньше занимаемая полоса, что позволяет отведенную для системы связи полосу частот уплотнить большим числом каналов;

требуется более узкая полоса пропускания приемника, что повышает помехозащищенность за счет снимания уровня помех в рабочей полосе частот

Вопросы для самоконтроля

1. Что такое модуляция?

2. Что называется информационными параметрами?

3. Что используется в качестве несущих колебаний?

4. Каким требованиям должны удовлетворять несущие колебания?

5. Какие основные виды модуляции вы знаете?

2. Методические указания к выполнению практической работы

«Расчет и построение спектра амплитудно-модулированного сигнала»

Цель работы: закрепить теоретический материал и выработать умения при расчете и построении спектра АМ сигнала.

Костров Б. В. Технологии физического уровня передачи данных. Учебник, -М.: Издательский центр «Академия», 2018. — 224с.

Ушаков П.А. Цепи и сигналы электросвязи. Учебник. –М.: Издательский центр «Академия», 2010. – 352с.

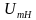
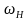
Задача: Рассчитать и построить спектр АМ сигнала, если = 8B; = 1π * рад/с; Ω = 2π* рад/с; m=25%.

1. Определить период колебаний несущей частоты (в с, мс, мкс)

= , = = 2* c = 0,2 мс

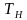
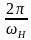
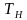
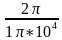
2. Определить значение несущей частоты (в Гц, в кГц, в МГц)

= = =0,5 * Гц = 5 кГц.

3. Определить период колебаний модулирующей частоты (в с, мс, мкс)

4. Определить значение модулирующей частоты (в Гц, в кГц, в МГц)

F = = = Гц = 1 КГц.

5. Определить приращение амплитуды при модуляции (В)

m = = m 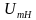= 0,25*8=2B.

6. Определить амплитуду боковых частот.

7. Определить значения боковых частот (в Гц, в кГц, в МГц).

8. Построить в масштабе спектральную диаграмму, ориентируясь на рис. 2е в лекции.

Видео:РТЦиС 2020. Лекция 13. Амплитудная модуляция гармонического колебания. Часть 1. Введение в модуляциюСкачать

Амплитудная модуляция: теория, временная и частотная области

Узнайте о самом простом способе кодирования информации в форме сигнала несущей частоты.

Мы видели, что радиочастотная модуляция представляет собой просто преднамеренную модификацию амплитуды, частоты или фазы синусоидального сигнала несущей частоты. Эта модификация выполняется в соответствии с конкретной схемой, которая реализуется передатчиком и понимается приемником. Амплитудная модуляция, которая, конечно, является источником термина «АМ радио», изменяет амплитуду несущей в соответствии с мгновенной величиной низкочастотного сигнала.

Видео:РТЦиС 2020. Лекция 14. Амплитудная модуляция гармонического колебания. Часть 2. Классическая АМСкачать

Математика

Математическое выражение амплитудной модуляции просто и интуитивно понятно: вы умножаете сигнал несущей на низкочастотный сигнал. Частота самой несущей не изменяется, но ее амплитуда будет постоянно изменяться в зависимости от величины низкочастотного сигнала. (Тем не менее, как мы увидим ниже, изменения амплитуды вводят новые частотные составляющие.) Здесь есть одна тонкая деталь – необходимость смещения низкочастотного сигнала; мы обсуждали это в предыдущей статье. Если у нас есть низкочастотный сигнал, который изменяется от -1 до +1, математическая зависимость может быть выражена следующим образом:

где x_ам – амплитудно-модулированный сигнал, x_нес – сигнал несущей частоты, а x_нч – низкочастотный сигнал. Мы можем пойти дальше, если рассматривать несущую как бесконечную синусоиду с фиксированной частотой и постоянной амплитудой. Если предположить, что амплитуда несущей равна 1, мы можем заменить x_нес на sin(ω_несt) .

Пока всё хорошо, но есть одна проблема с этими связями: у вас нет контроля над «интенсивностью» модуляции. Другими словами, связь между изменением низкочастотного сигнала и изменением сигнала несущей частоты является фиксированной. Мы не можем, например, сконструировать систему таким образом, чтобы небольшое изменение в величине низкочастотного сигнала создавало значительное изменение амплитуды несущей. Чтобы устранить это ограничение, введем m , известный как индекс модуляции.

Теперь, изменяя m , мы можем контролировать интенсивность влияния низкочастотного сигнала на амплитуду несущей. Однако, обратите внимание, что m умножается на исходный, а не на смещенный низкочастотный сигнал. Таким образом, если x_нч изменяется от -1 до +1, любое значение m больше 1 приведет к тому, что (1 + mx_нч) будет заходить на отрицательный участок оси y, но это именно то, чего мы пытались избежать, сдвинув сперва низкочастотный сигнал вверх. Поэтому помните, что если используете индекс модуляции, сигнал должен быть смещен на максимальную амплитуду mx_нч , а не на x_нч .

Видео:РТЦиС 2020. Лекция 15. Амплитудная модуляция гармонического колебания. Часть 3. Балансная АМСкачать

Временна́я область

Мы рассмотрели формы амплитудно-модулированных сигналов во временно́й области в предыдущей статье. Последней была следующая диаграмма (низкочастотный сигнал – красный, амплитудно-модулированная несущая – синий):

Несущая, умноженная на смещенный низкочастотный сигнал

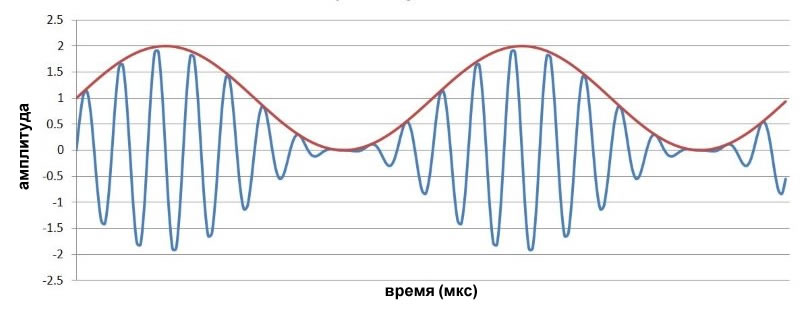
Теперь давайте посмотрим на влияние индекса модуляции. Вот аналогичный график, но на этот раз я сдвинул низкочастотный сигнал, добавив 3 вместо 1 (исходный размах всё еще составляет от -1 до +1).

Несущая, умноженная на смещенный низкочастотный сигнал

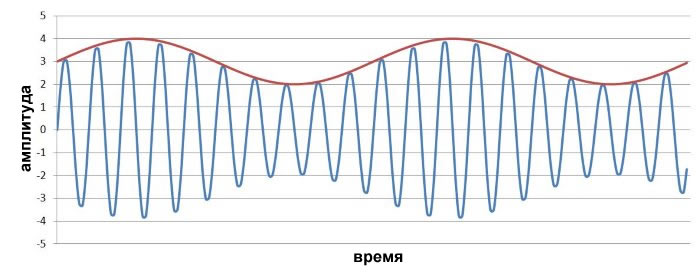
Теперь включим индекс модуляции. На следующем графике m = 3.

Несущая, умноженная на смещенный низкочастотный сигнал

Амплитуда несущей теперь «более чувствительна» к изменению величины низкочастотного сигнала. Смещенный низкочастотный сигнал не заходит на отрицательную часть оси y, потому что я выбрал смещение по постоянному напряжению в соответствии с индексом модуляции.

Возможно, вам интересно, как выбрать правильное смещение по постоянному напряжению, не зная точных амплитудных характеристик низкочастотного сигнала? Другими словами, как мы можем гарантировать, что отрицательная волна низкочастотного сигнала доходит точно до нуля? Ответ: вам это не нужно. Предыдущие два графика являются одинаково допустимыми формами амплитудно-модулированного сигнала; низкочастотный сигнал корректно передается в обоих случаях. Любое смещение по постоянному напряжению, которое остается после демодуляции, легко удаляется с помощью последовательно включенного конденсатора (следующая глава будет посвящена демодуляции).

Видео:Амплитудная модуляция АМ (математическая модель и спектр)Скачать

Частотная область

Как обсуждалось во второй статье данного миниучебника, радиочастотное проектирование широко использует анализ в частотной области. Мы может проверять и оценивать реальный модулированный сигнал, измеряя его с помощью анализатора спектра, но это означает, что нам нужно знать, как должен выглядеть спектр.

Начнем с представления сигнала несущей частоты в частотной области:

Спектр несущей

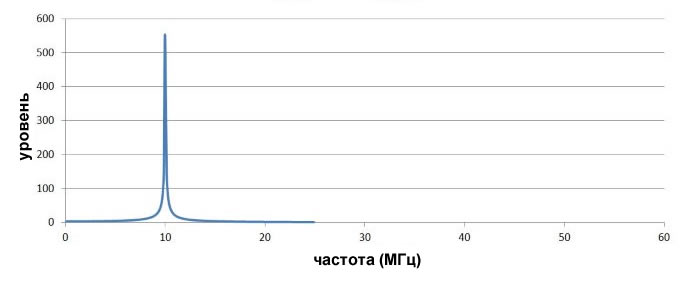
Это именно то, что мы ожидаем от немодулированной несущей: один всплеск на частоте 10 МГц. Теперь давайте посмотрим на спектр сигнала, создаваемого амплитудной модуляцией сигнала несущей частоты с помощью синусоиды с постоянной частотой 1 МГц.

Спектр амплитудно-модулированного сигнала

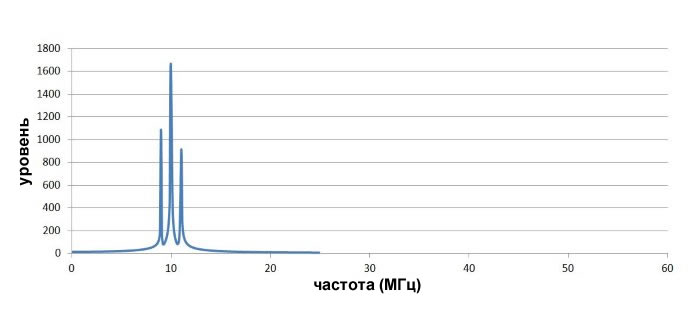
Здесь вы видите стандартные характеристики амплитудно-модулированного сигнала: низкочастотный сигнал сдвинут в соответствии с частотой несущей. Вы могли бы также подумать об этом как о «добавлении» частот низкочастотного сигнала к сигналу несущей, что мы и делаем, когда используем амплитудную модуляцию – несущая остается, как вы можете видеть на сигналах во временной области, но амплитудные изменения образовывают новые частотные составляющие, которые соответствуют спектральным характеристикам низкочастотного сигнала.

Если мы посмотрим более внимательно на спектр модулированного сигнала, то увидим, что два новых пика составляют 1 МГц (т.е. частота низкочастотного сигнала) выше и 1 МГц ниже несущей частоты:

Спектр амплитудно-модулированного сигнала

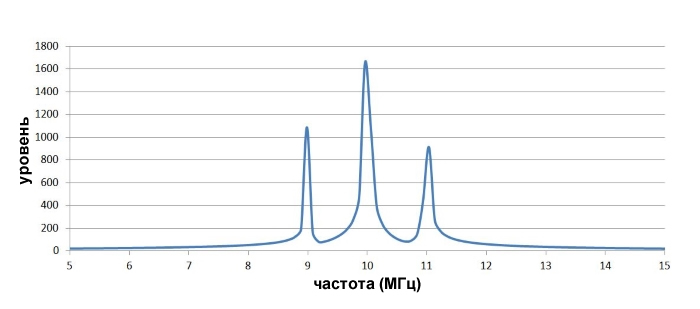
(В случае, если вам интересно, асимметрия является артефактом процесса вычисления, эти графики были созданы с использованием реальных данных и с ограниченным разрешением. Идеализированный спектр был бы симметричным.)

Видео:Амплитудная модуляцияСкачать

Отрицательные частоты

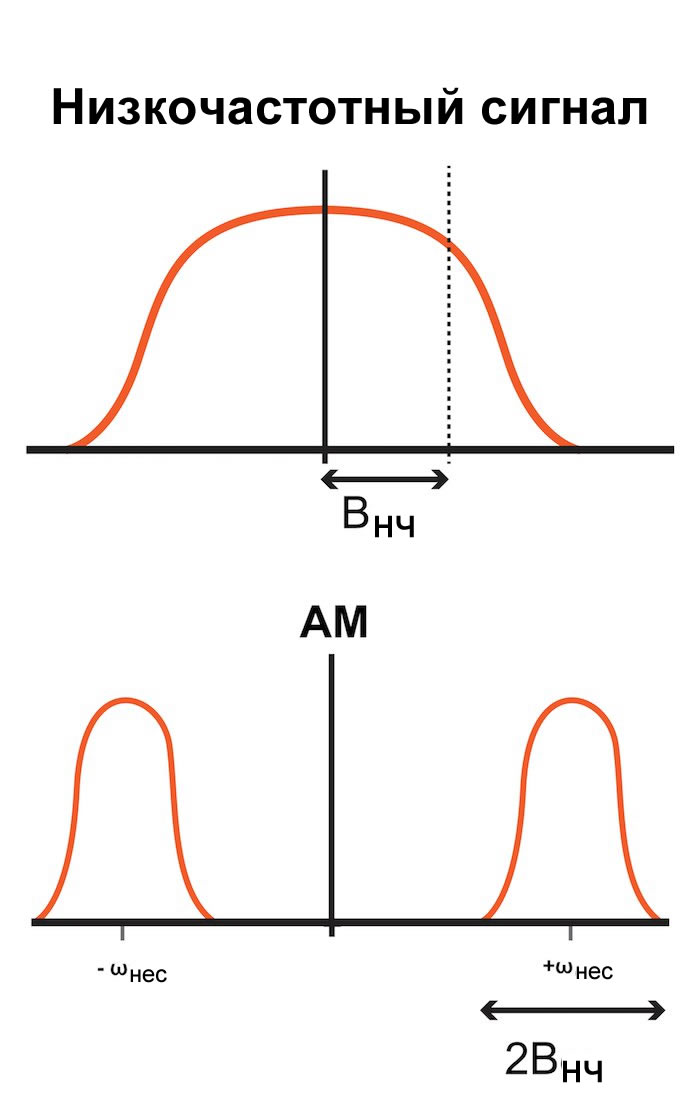
Резюмируя, амплитудная модуляция переносит спектр низкочастотного сигнала в полосу частот с центром на несущей частоте. Однако есть кое-что, что нам нужно объяснить: почему получилось два пика – один на несущей частоте плюс частота низкочастотного сигнала, а другой на несущей частоте минус частота низкочастотного сигнала? Ответ становится ясным, если мы просто вспомним, что спектр Фурье симметричен относительно оси y; хотя мы часто показывает только положительные частоты, отрицательная часть оси x содержит соответствующие отрицательные частоты. Эти отрицательные частоты легко игнорируются, когда мы имеем дело с исходным спектром, но при смещении спектра важно их учесть.

Следующая диаграмма должна прояснить эту ситуацию:

Отрицательные частоты

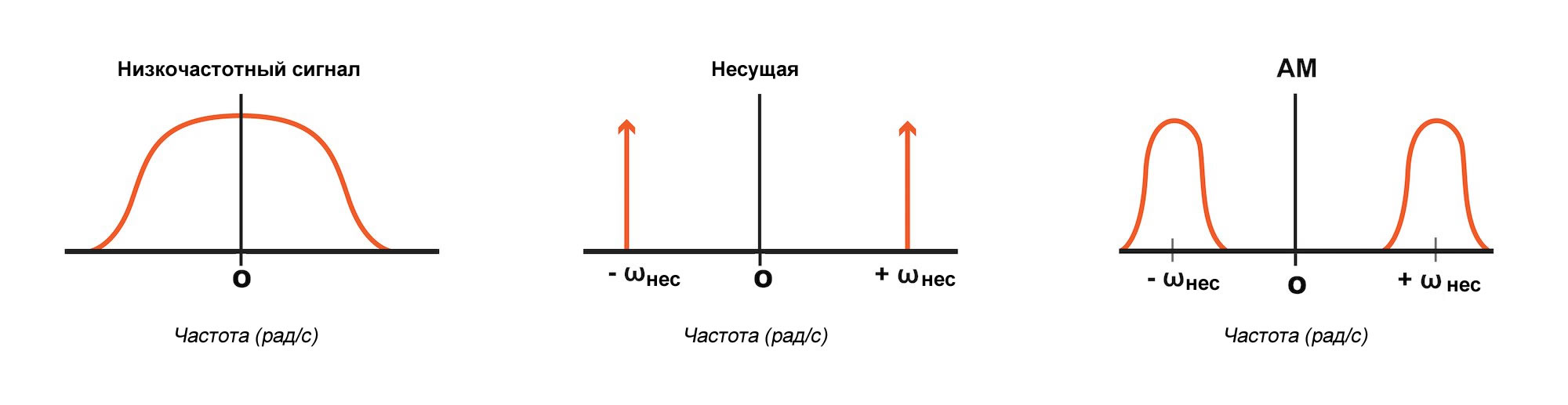
Как вы можете видеть, спектр низкочастотного сигнала и спектр несущей частоты симметричны относительно оси y. Для низкочастотного сигнала это приводит к спектру, который непрерывно продолжается от положительной части оси x до отрицательной часть, в случае несущей мы просто имеем два пика, один на +ω_нес и один на -ω_нес . И спектр амплитудно-модулированного сигнала, опять-таки, симметричный: перенесенный спектр низкочастотного сигнала появляется и в положительной, и в отрицательной частях оси x.

И еще одна вещь, которую следует иметь в виду: амплитудная модуляция увеличивает ширину полосы сигнала в два раза. Мы измеряем ширину полосы только для положительных частот, поэтому ширина полосы равна просто B_нч (смотрите диаграмму ниже). Но после переноса всего спектра (положительных и отрицательных частот), все исходные частоты становятся положительными, поэтому ширина полосы модулированного сигнала равна 2B_нч .

Ширина полосы АМ сигнала

Видео:Частотное и временное представление сигналов. Спектр. МодуляцияСкачать

Что такое модуляция и разновидности модулированных сигналов?

Общие сведения о модуляции

Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.

В результате модуляции сигналы переносятся в область более высоких частот.

Использование модуляции позволяет:

• согласовать параметры сигнала с параметрами линии;
• повысить помехоустойчивость сигналов;
• увеличить дальность передачи сигналов;
• организовать многоканальные системы передачи (МСП с ЧРК).

Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

Рисунок 1 — Условное графическое обозначение модулятора

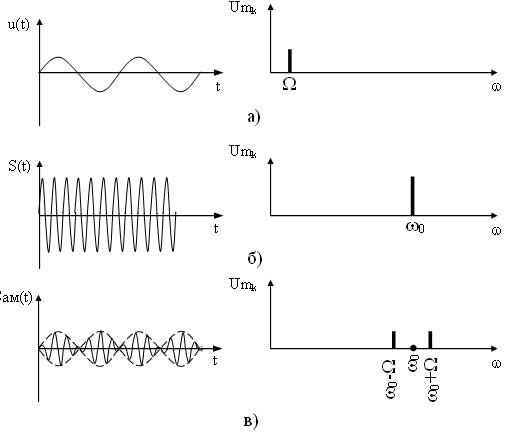
При модуляции на вход модулятора подаются сигналы:

u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);

S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w₀ или f₀);

Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.

В качестве несущего сигнала может использоваться:

• гармоническое колебание, при этом модуляция называется аналоговой или непрерывной;
• периодическая последовательность импульсов, при этом модуляция называется импульсной;
• постоянный ток, при этом модуляция называется шумоподобной.

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.

1. Виды аналоговой модуляции:

• амплитудная модуляция (АМ), происходит изменение амплитуды несущего колебания;
• частотная модуляция (ЧМ), происходит изменение частоты несущего колебания;
• фазовая модуляция (ФМ), происходит изменение фазы несущего колебания.

2. Виды импульсной модуляции:

• амплитудно-импульсная модуляция (АИМ), происходит изменение амплитуды импульсов несущего сигнала;
• частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
• Фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
• Широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.

Амплитудная модуляция

Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

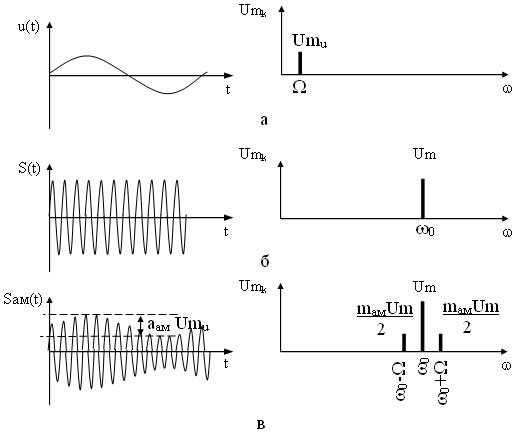
Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение амплитуды несущего сигнала по закону:

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Вынесем Um за скобки:

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?₀—? называется нижней боковой составляющей, а на частоте ?₀ + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

Рисунок 2 — Временные и спектральные диаграммы модулирующего (а), несущего (б) и ампдтудно-модулированного (в) сигналов

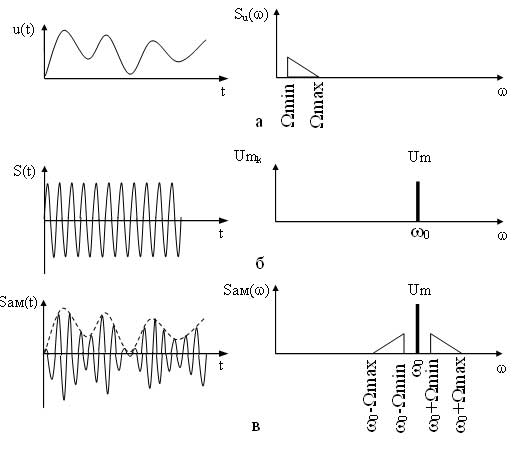
Ширина спектра для данного сигнала будет определятся

Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Рисунок 3 — Временные и спектральные диаграммы сигналов при случайном модулирующем сигнале

Ширина спектра для данного сигнала будет определятся

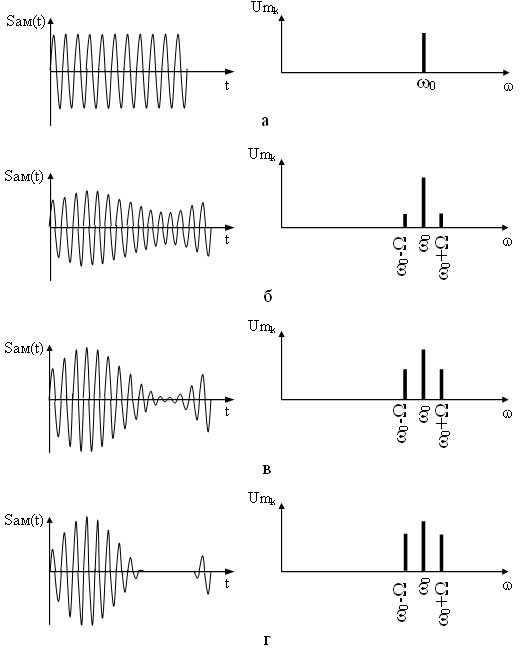
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

Рисунок 4 — Временные и спектральные диаграммы АМ сигналов при различных mам: а) при mам=0, б) при mам=0,5, в) при mам=1, г) при mам>1

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

• узкая ширина спектра АМ сигнала;
• простота получения модулированных сигналов.

Недостатками этой модуляции являются:

• низкая помехоустойчивость (т. к. при воздействии помехи на сигнал искажается его форма — огибающая, которая и содержит передаваемое сообщение);
• неэффективное использование мощности передатчика (т. к. наибольшая часть энергии модулированного сигнала содержится в составляющей несущего сигнала до 64%, а на информационные боковые полосы приходится по 18%).

Амплитудная модуляция нашла широкое применение:

• в системах телевизионного вещания (для передачи телевизионных сигналов);
• в системах звукового радиовещания и радиосвязи на длинных и средних волнах;
• в системе трехпрограммного проводного вещания.

Балансная и однополосная модуляция

Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.

Рисунок 5 — Временные и спектральные диаграммы модулирующего (а), несущего (б) и балансно-модулированного (в) сигналов

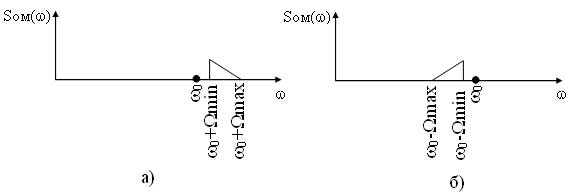
Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.

Рисунок 6 — Спектральные диаграммы однополосно-модулированных сигналов: а) с верхней боковой полосой (ВБП), б) с нижней боковой полосой (НБП)

Частотная модуляция

Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение частоты несущего сигнала по закону:

где а_чм — коэффициент пропорциональности частотной модуляции.

Поскольку значение sin ? t может изменятся в диапазоне от -1 до 1, то наибольшее отклонение частоты ЧМ сигнала от частоты несущего сигнала составляет

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

Значение ? _чм(t) непосредственно подставить в S(t) нельзя, т. к. аргумент синуса ? t+j является мгновенной фазой сигнала ?(t) которая связана с частотой выражением

Отсюда следует что, чтобы определить ?_чм(t) необходимо проинтегрировать ?_чм(t)

Причем в выражении (12) ? является начальной фазой несущего сигнала.

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

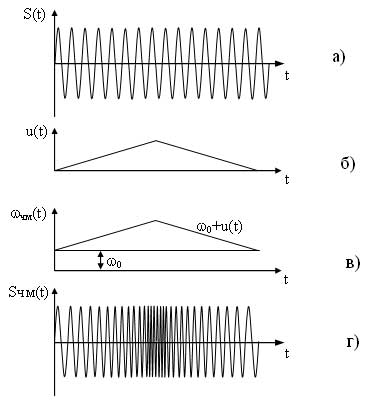
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

Рисунок 7 — Формирование ЧМ сигнала

Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

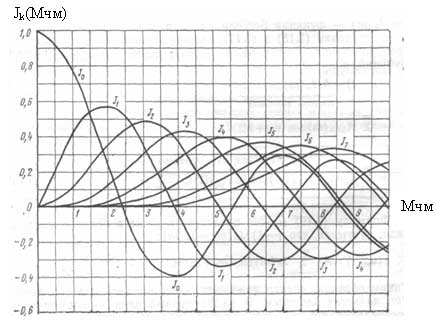
где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

Рисунок 8 — Функции Бесселя

видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

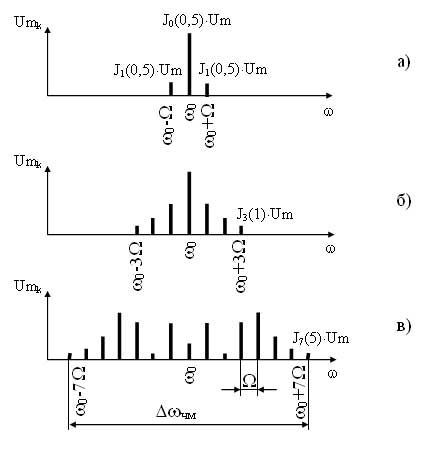
Поскольку увеличение составляющих приводит к увеличению ширины спектра ЧМ сигнала, то значит, ширина спектра зависит от Мчм (рисунок 9). Как видно из рисунка, при Мчм ?0,5 ширина спектра ЧМ сигнала соответствует ширине спектра АМ сигнала и в этом случае частотная модуляция является узкополосной, при увеличении Мчм ширина спектра увеличивается, и модуляция в этом случае является широкополосной. Для ЧМ сигнала ширина спектра определяется

Достоинством частотной модуляции являются:

• высокая помехоустойчивость;
• более эффективное использование мощности передатчика;
• сравнительная простота получения модулированных сигналов.

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

• в системах телевизионного вещания (для передачи сигналов звукового сопровождения);
• системах спутникового теле- и радиовещания;
• системах высококачественного стереофонического вещания (FM диапазон);
• радиорелейных линиях (РРЛ);
• сотовой телефонной связи.

Рисунок 9 — Спектры ЧМ сигнала при гармоническом модулирующем сигнале и при различных индексах Мчм: а) при Мчм=0,5, б) при Мчм=1, в) при Мчм=5

Фазовая модуляция

Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение мгновенной фазы несущего сигнала по закону:

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

Произведение а_фмUm_u?=??_m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

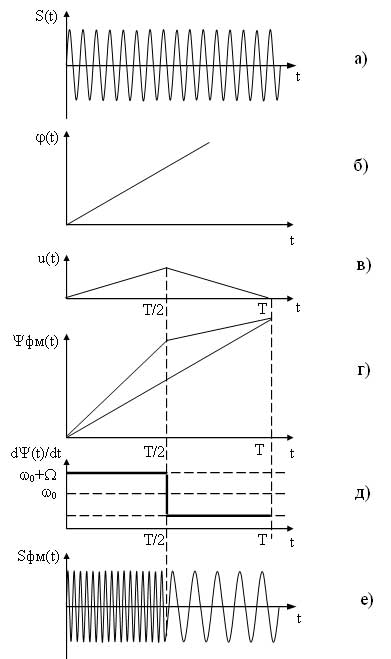
Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

При разложении математической модели ФМ сигнала на гармонические составляющие получится такой же ряд, как и при частотной модуляции (15), с той лишь разницей, что коэффициенты J_k будут зависеть от индекса фазовой модуляции ? ?_m (J_k(? ?_m)). Определятся эти коэффициенты будут аналогично, как и при ЧМ, т. е. по функциям Бесселя, с той лишь разницей, что по оси абсцисс необходимо заменить Мчм на ? ?_m. Поскольку спектр ФМ сигнала строится аналогично спектру ЧМ сигнала, то для него характерны те же выводы что и для ЧМ сигнала (пункт 1.4).

Рисунок 10 — Формирование ФМ сигнала

Ширина спектра ФМ сигнала определяется выражением:

Достоинствами фазовой модуляции являются:

• высокая помехоустойчивость;
• более эффективное использование мощности передатчика.
• недостатками фазовой модуляции являются:

• большая ширина спектра;
• сравнительная трудность получения модулированных сигналов и их детектирование

Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

• амплитудную манипуляцию (АМн или АМТ);
• частотную манипуляцию (ЧМн или ЧМТ);
• фазовую манипуляцию (ФМн или ФМТ);
• относительно-фазовую манипуляцию (ОФМн или ОФМ).

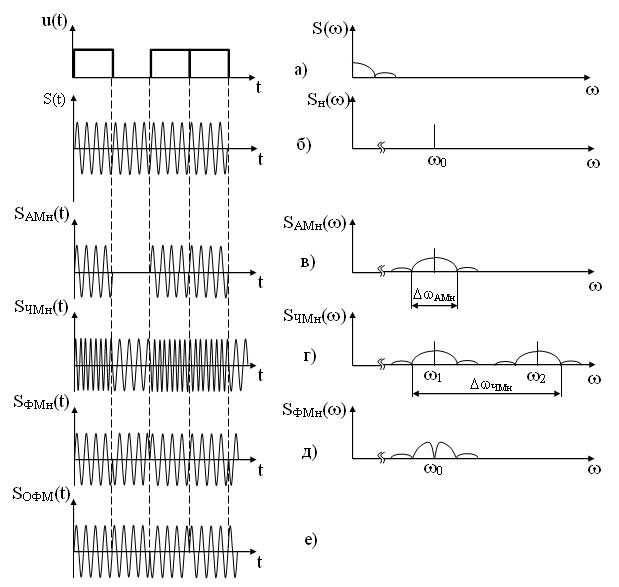
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При частотной манипуляции используются две частоты ?₁ и ?₂. При наличии импульса в модулирующем сигнале (посылке) используется более высокая частота ?₂, при отсутствии импульса (активной паузе) используется более низкая частота w₁ соответствующая немодулированной несущей (рисунок 11, г)). Спектр частотно-манипулированного сигнала S_ЧМн(t) имеет две полосы возле частот ?₁ и ?₂.

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

Рисунок 11 — Временные и спектральные диаграммы модулированных сигналов различных видов дискретной двоичной модуляции

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

Импульсная модуляция

Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.

Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:

• амплитудно-импульсная модуляция (АИМ); происходит изменение амплитуды импульсов несущего сигнала;
• частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
• фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
• широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.

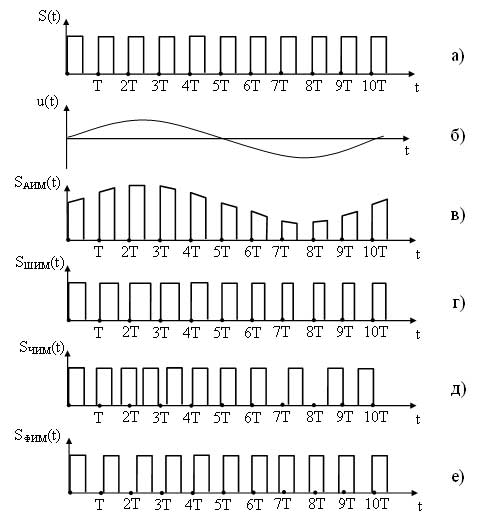
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.

При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).

При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).

Рисунок 12 — Временные диаграммы сигналов при импульсной модуляции

При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).

При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.

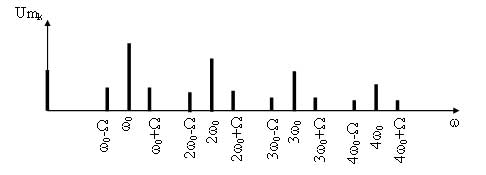
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.

Рисунок 13 — Спектр импульсно-модулированного сигнала

Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.

Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f₀ =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.

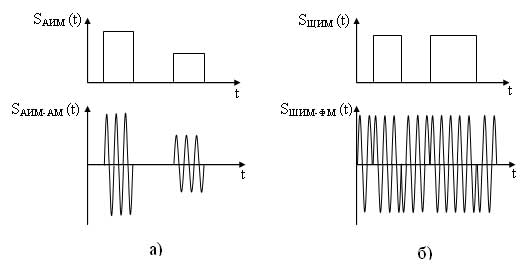
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.

Рисунок 14 — Временные диаграммы сигналов при импульсной повторной модуляции

📽️ Видео

Амплитудная модуляцияСкачать

Модуляция, детектирование. 11 класс.Скачать

Теория: радиоволны, модуляция и спектр.Скачать

UML Временная Диаграмма (UML Timing Diagram)Скачать

Модуляция. Базовые понятияСкачать

КАК ПРОИСХОДИТ РАДИОПЕРЕДАЧА И РАДИОПРИЁМ. АМПЛИТУДНАЯ И ЧАСТОТНАЯ МОДУЛЯЦИЯ [РадиолюбительTV 15]Скачать

Что такое амплитудная, частотная и ШИМ модуляцияСкачать

ПППИСкачать

Амплитудный модулятор. Амплитудный детектор.Скачать

Виды модуляцииСкачать

Аналоговая модуляция. АМ ЧМ ФМСкачать

AGalilov: Преобразование Фурье "на пальцах"Скачать

Потенциальная диаграммаСкачать