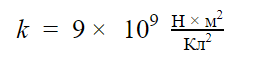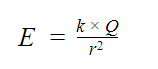Амплитуда напряженности электрического поля уравнение

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Амплитуда напряженности электрического поля уравнение

амплитуда напряженности электрического поля

В вакууме вдоль оси χ распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны равна 1 мА/м. Определите амплитуду напряженности электрического поля волны.

В однородной изотропной среде с диэлектрической проницаемостью, равной 2, и магнитной проницаемостью, равной 1, распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 50 В/м. Найти амплитуду напряженности магнитного поля и фазовую скорость волны.

Плоская электромагнитная волна распространяется в однородной и изотропной среде с ε = 2 и μ = 1. Амплитуда напряженности электрического поля волны Е₀ = 12 В/м. Определить: 1) фазовую скорость волны; 2) амплитуду напряженности магнитного поля волны.

Угол между направлением распространения плоской электромагнитной волны и поверхностью, на которую в воздухе падает волна, равна α = 30°. Давление, которое вызывает волна на поверхность, равна p = 60·10 –20 Н/м 2 . Найти коэффициент отражения R поверхности, если амплитуда напряженности электрического поля Е_m = 0,4 мВ/м.

В однородной изотропной среде с относительной диэлектрической проницаемостью ε и относительной магнитной проницаемостью μ, близкой к единице, распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны равна Е_m, амплитуда напряженности магнитного поля — H_m = 7,66·10 –3 А/м, фазовая скорость распространения волны — υ = 2,76·10 8 м/с. Найти ε, E_m.

Амплитуда напряженности электрического поля плоской электромагнитной волны равна 1000 В/м. Какова амплитуда напряженности магнитного поля этой же волны?

Какова интенсивность электромагнитной волны в вакууме, если амплитуда напряженности ее электрического поля составляет 27,5 В/м.

В вакууме вдоль оси X распространяется плоская электромагнитная волна, амплитуда напряженности магнитного поля которой равна 0,05 А/м. Какова амплитуда напряженности электрического поля волны и ее интенсивность?

В однородной изотропной среде с ε = 3 и μ = 1 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля которой Е = 10 В/м. Найти амплитуду напряженности магнитного поля и фазовую скорость волны.

В вакууме вдоль оси X распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны H₀ = 5·10 –2 А/м. Определить: а) амплитуду напряженности электрического поля волны E₀; б) среднюю по времени плотность энергии волны w.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 8,56·10 –3 А/м. Фазовая скорость распространения волны — v = 1,86·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,6 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 2,14·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 2,5 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 2,12·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 6,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,6 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 1,88·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 6,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 1,0 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 7,96·10 –3 А/м. Фазовая скорость распространения волны — v = 3,0·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,4 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 2,12·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 1,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 1,5 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,1 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 1,224·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 4,28·10 –3 А/м. Фазовая скорость распространения волны — v = 1,86·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 3,0·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 2,0 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 2,12·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,6 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 0,856·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 6,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,5 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 26,0·10 –3 А/м. Фазовая скорость распространения волны — v = 1,224·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 7,51·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,6 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,8 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 1,327·10 –3 А/м. Фазовая скорость распространения волны — v = 3,0·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 3,0 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 2,12·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 6,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 0,2 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 1,5 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 1,224·10 8 м/с. Найти ε, H_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 1,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 5,31·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 1,06·10 –3 А/м. Фазовая скорость распространения волны — v = 3,0·10 8 м/с. Найти ε, E_m.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 2,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m, амплитуда напряженности магнитного поля равна H_m = 2,25·10 –3 А/м. Фазовая скорость распространения волны — v. Найти E_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε = 6,0 распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 1,2 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v. Найти H_m, v.

В однородной изотропной немагнитной среде с относительной диэлектрической проницаемостью ε распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля равна E_m = 4,0 В/м, амплитуда напряженности магнитного поля равна H_m. Фазовая скорость распространения волны — v = 3,0·10 8 м/с. Найти ε, H_m.

Плоская электромагнитная волна, имеющая амплитуду напряженности электрического поля 0,12 В/м, распространяется в среде, диэлектрическая проницаемость которой ε = 2 и магнитная проницаемость μ = 1. Определить уравнение электромагнитной волны с числовыми коэффициентами, произвольно выбрав начальные условия. Частота волны 10 5 Гц. Определить среднее значение вектора Пойнтинга.

Видео:НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Напряженность электрического поля

О чем эта статья:

8 класс, 10 класс

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Что такое электрическое поле

Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.

Видео:Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

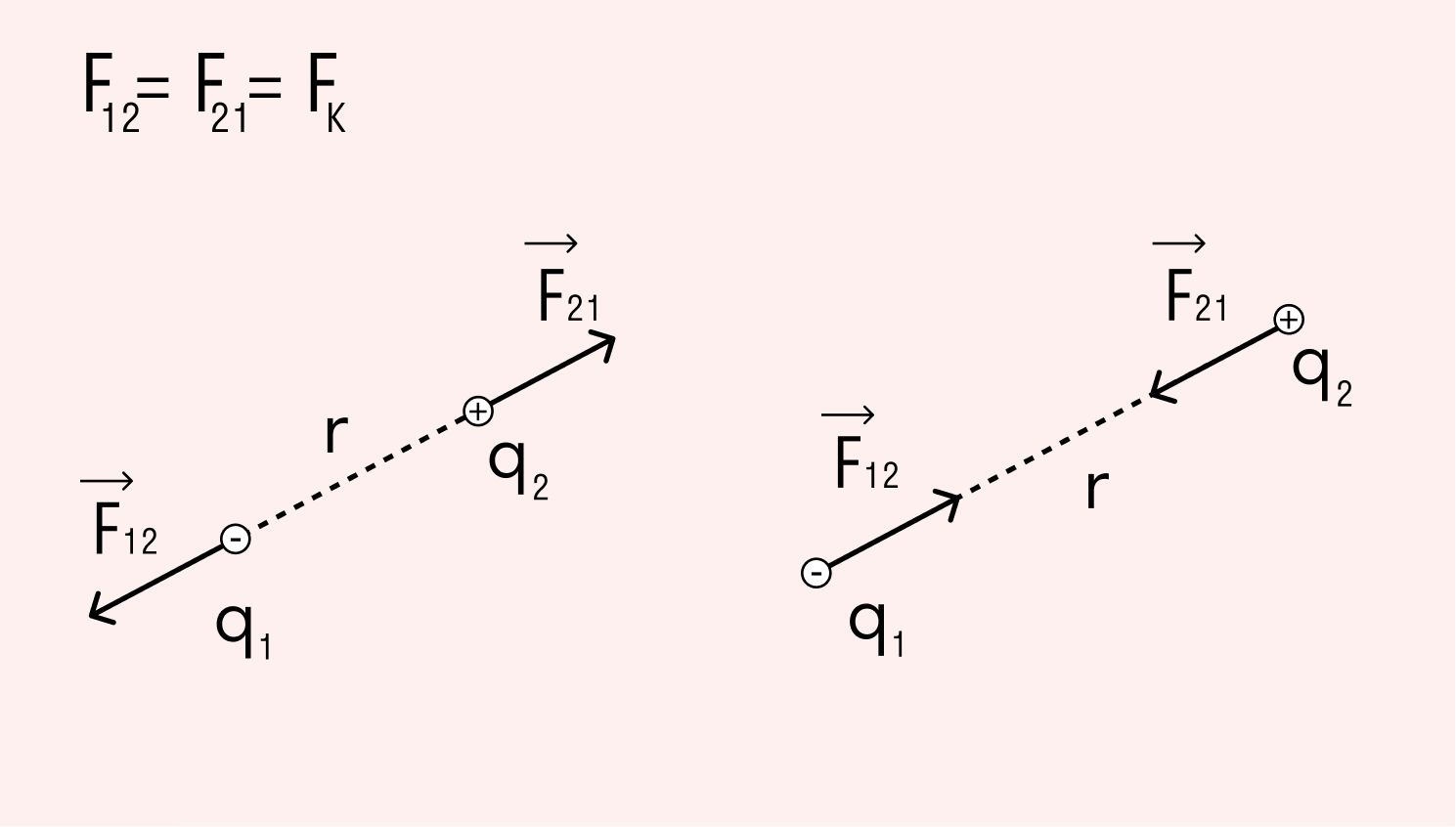
Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление.

Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

расстояние между зарядами очень мало — порядка 10 -15 м;

речь идет о сверхсильных полях с напряженностью более 10 20 в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Видео:Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.

Закон Кулона

Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: 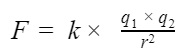где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Видео:Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

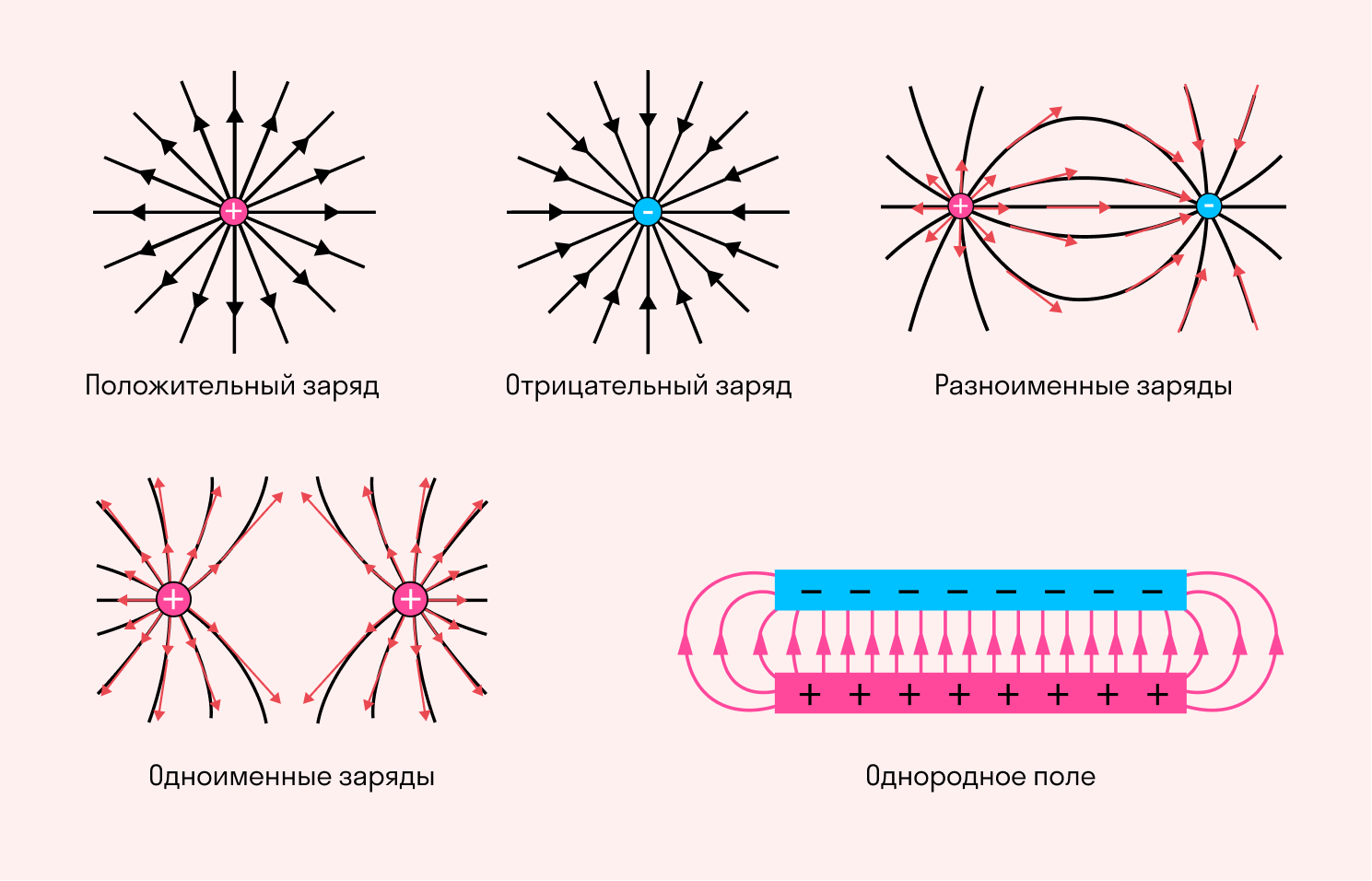
Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Видео:Билет №04 "Потенциал электростатического поля"Скачать

Методы измерения основных параметров, характеризующих высокочастотное электромагнитное поле

Страницы работы

Содержание работы

Методы измерения основных параметров, характеризующих высокочастотное электромагнитное поле

Общие сведения

Электромагнитное поле характеризуется рядом параметров, но в условиях учеб­ной лаборатории обычно измеряют напряженность электрического поля или ве­­­личину, про­пор­­­циональную квадрату напряженности (мощность), а также плот­но­сть потока мощнос­ти, т.е. мощность, приходящуюся на единицу площади неко­то­­рой поверхности. Везде мы рас­сматриваем только процессы, изменяющиеся во вре­мени по гармоническому закону. Поэтому все величины, в том числе и нап­ря­жен­ность электрического поля, изменяются во вре­мени по закону .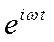

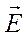
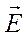
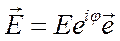
Напряженность электрического поля – это в общем случае векторная ком­п­ле­к­­­с­ная величина, которая характеризуется амплитудой, фазой и поляризацией, т.е. ориентацией вектора в пространстве. В соответствии с этим можно за­пи­сать , где E – амплитуда напряженности электрического поля (в системе еди­ниц СИ она изме­ря­ет­ся в вольтах на метр);

j – фаза напряженности электрического поля;

– поляризация, т.е. ориентация вектора электрического поля.

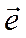
Измерение амплитуды напряженности поля

Рассмотрим измерение амплитуды напряженности электрического поля. Во мно­гих слу­чаях нам не обязательно знать абсолютное значение амплитуды нап­ря­жен­ности (в во­ль­тах на метр), а достаточно знать, как изменяется амплитуда нап­ря­женности поля при пе­ре­мещении из одной точки пространства в другую. Такие из­мерения называются отно­си­те­льными.

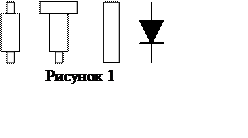При измерениях напряженности электрического поля используется устройство, на­­зы­ва­емое зондом. Имеется ряд вариантов конструкции зонда (они рассмотрены ни­же), но все они обязательно содержат элемент, называемый детектором. Де­те­к­тор предназначен для преобразова­ния высокочастотных модулированных ко­ле­ба­ний в низкочастотные (ко­ле­бания с час­тотой мо­ду­ляции) или для преобразо­ва­ния вы­­со­кочастотных немодулиро­ван­ных коле­баний в постоянное напряжение (ток). На СВЧ в качестве детекторов, как пра­­ви­ло, ис­пользуются полупроводнико­вые дио­­ды, конструкция которых изобра­же­на на рисунке 1. Там же показано изобра­же­ние де­­тектора на принципиаль­ной схеме, кото­­рое будет использоваться в даль­ней­шем.

При измерениях чаще всего ис­по­ль­­зуются следующие ва­рианты конструк­ции зон­дов:

1). Зонд в виде электрического ди­по­ля Герца или сим­мет­ричного электри­че­с­ко­го вибратора. Диполь Герца и плечи вибратора должны быть ори­ен­тированы па­­раллельно линиям вектора 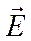измеряе­мого поля. В качестве плеч дипо­ля Герца или симметричного вибратора на СВЧ можно использовать выводы полуп­ровод­ни­­­­кового диода (рисунок 2-а).

2). Зонд в виде специальной детекторной секции волноводного типа (рисунок 2-б). В этом случае детектор устанавливается в прямоугольном волноводе, который иг­ра­ет роль при­­емной антенны. Вектор 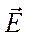измеряемого поля должен быть пер­пен­ди­ку­лярен широкой стенке волновода.

3). Зонд, состоящий из приемной антенны малых размеров (обычно – пира­ми­да­­ль­но­го рупора), присоединенный к детекторной секции (рисунок 2-в). Ориентация век­тора 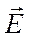та­кая же, как и в предыдущем случае.

4). Зонд, состоящий из приемной антенны в виде несимметричного вибратора (обы­­ч­но – это штырь, помещенный в волновод или объемный резонатор), при­со­е­ди­нен­но­го к де­тек­торной секции коаксиального типа (рисунок 2-г). Вектор 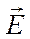из­ме­ря­е­мого поля при этом дол­жен быть параллелен штырю.

Первые 3 варианта зонда используются для измерения амплитуды нап­ряжен­но­с­ти по­ля или мощности в различных точках пространства (в том числе – и в рас­крыве из­луча­ю­щего волновода или рупора). Четвертый вариант обычно исполь­зу­ет­ся для измерения рас­пределения амплитуды напряженности поля вдоль волно­вода или объемного ре­зо­на­то­ра. Зонд в виде штыря при этом перемещается вдоль ще­ли, прорезанной в стенке вол­но­во­да или резонатора.

Любой зонд, помещенный в некоторую точку, в которой мы хотим измерить нап­ря­же­н­­ность электрического поля, искажает поле в этой точке. Для того, чтобы это иска­же­ние было малым, необходимо, чтобы размер зонда был мал по срав­не­нию с длиной волны.

Аппаратура для измерения абсолютной и относительной амплитуды нап­ря­жен­но­с­ти по­ля

При измерении абсолютной амплитуды напряженности поля измерительный зонд (при­емная антенна) присоединяется к специальной измерительной аппа­ра­ту­ре. Чаще все­го используются два вида аппаратуры:

1). Высокочувствительный приемник, снабженный индикатором выхода. Для ка­­­либровки усиления такого приемника используется метод сравнения (компари­рования), поэ­­­тому такие приемники называют компараторами.

2). Высокочастотный микровольтметр. Он также содержит высоко­чувствитель­ный при­емник с индикатором выхода и устройство для калибровки усиления. Де­тек­тор при этом конструктивно входит в состав компаратора или мик­рово­льт­мет­ра.

При измерении относительной амплитуды напряженности поля используют один из выше перечисленных вариантов конструкции зонда с детектором. Сигнал, при­нятый зон­дом, после детектора подается на индикатор, который фиксирует из­меряемую вели­чи­ну. Используемые индикаторы могут быть 2-х типов:

1). Приборы постоянного тока (микроамперметры, миллиамперметры) или уси­ли­­те­ли постоянного тока, снабженные индикатором выхода.

2). Усилители переменного низкочастотного напряжения, снабженные инди­ка­то­ром выхода.

💡 Видео

Урок 219. Задачи на напряженность электрического поля - 1Скачать

Лекция 2 ВолныСкачать

О чем говорят уравнения Максвелла? Видео 1/2Скачать

Физика 11 класс (Урок№10 - Электромагнитные волны.)Скачать

Урок 223. Теорема ГауссаСкачать

Электрическое поле. Теорема ГауссаСкачать

4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Билет №34 "Электромагнитные волны"Скачать

Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

3.2 Уравнения монохроматического электромагнитного поляСкачать

3.1 Система уравнений монохроматического электромагнитного поляСкачать

Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать