Содержание:
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Алгоритм решения произвольной системы линейных уравнений
- Метода Гаусса: примеры решения СЛАУ
- Метод Гаусса — что это такое?
- Основные определения и обозначения
- Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)
- Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы
- 📺 Видео
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Алгоритм решения произвольной системы линейных уравнений
Решение произвольных систем
Пусть дана система m линейных уравнений с n неизвестными:
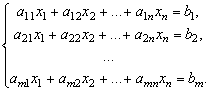
В матричной форме система (1) имеет вид
где А = 
Х = 
В = 
Решением системы (1) называется всякий вектор 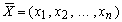
Система уравнений, имеющая хотя бы одно решение, называется совместной. Система уравнений называется несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы называются эквивалентными, если множества их решений совпадают.
Теорема 1. (теорема Кронекера — Капелли ). Система (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы:
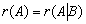
Теорема 2 . Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесконечно много решений.
Пусть ранг матрицы r ( A )= r n . Переменные называются базисными (основными), если определитель матрицы коэффициентов при них (базисный минор) отличен от нуля. Количество базисных переменных равно r . Другие n — r переменных называются свободными ( неосновными ). Выражение базисных переменных через свободные называется общим решением системы. Из него можно получить бесконечное множество частных решений, придавая свободным переменным произвольные значения.
Решение системы (1), в котором свободные переменные имеют нулевые значения, называется базисным решением. Число различных базисных решений не превосходит 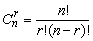
Метод последовательного исключения неизвестных
Метод Гаусса — это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1.
Элементарными преобразованиями системы являются:
— умножение уравнения на число, отличное от нуля;
— сложение уравнения, умноженного на любое число, с другим уравнением;
— отбрасывание уравнения 0 = 0.
Если при выполнении элементарных преобразований получено уравнение вида 0 = k (где k 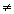
Перейдем теперь к решению систем с различным количеством неизвестных и уравнений. Пусть дана система m линейных уравнений с n неизвестными. Если такая система совместна, то при r n она имеет бесконечное множество решений, каждое из которых может быть получено из общего решения системы.
Для нахождения общего решения нам необходимо выбрать, какие неизвестные мы будем считать основными (базисными). Это могут быть любые r переменных, коэффициенты при которых составляют определитель, отличный от нуля. Затем выбранные основные переменные нужно выразить через свободные. Для этого с помощью элементарных преобразований необходимо расширенную матрицу системы привести к такому виду, чтобы коэффициенты при базисных переменных образовали так называемые базисные столбцы — столбцы, состоящие из нулей и одной единицы.
Решение систем линейных уравнений методом последовательного исключения неизвестных можно оформлять в виде таблицы.
Левый столбец таблицы содержит информацию об исключенных (базисных) переменных. Остальные столбцы содержат коэффициенты при неизвестных и свободные члены уравнений.
В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению очередной итерации:
1. Выбирают переменную 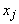
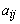
2. Элементы ключевой строки делят на ключевой элемент.
3. Ключевой столбец заполняют нулями.
4. Остальные элементы вычисляют по правилу прямоугольника: составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали и полученную разность делят на ключевой элемент.
Переход к другому базису
Перейти от одного базиса системы к другому позволяет преобразование однократного замещения: вместо одной из основных переменных в базис вводят одну из свободных переменных. Для этого в столбце свободной переменной выбирают ключевой элемент и выполняют преобразования по указанному выше алгоритму, начиная с п. 2.
Нахождение опорных решений
Опорным решением системы линейных уравнений называется базисное решение, не содержащее отрицательных компонент.
Опорные решения системы находят методом Гаусса при выполнении следующих условий.
1. В исходной системе все свободные члены должны быть неотрицательны: 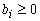
2. В число базисных может быть введена только та переменная, в столбце коэффициентов при которой есть хотя бы один положительный элемент.
3. Если при переменной, вводимой в базис, имеются положительные коэффициенты в нескольких уравнениях, то переменная вводится в базис в то уравнение, которому соответствует наименьшее в столбце отношение свободных членов к этим положительным коэффициентам.
Замечание 1 . Если в процессе исключения неизвестных появится уравнение, в котором все коэффициенты неположительны , а свободный член 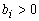
Замечание 2 . Если в столбцах коэффициентов при свободных переменных нет ни одного положительного элемента, то переход к новому опорному решению невозможен.
Видео:Решение системы уравнений методом ГауссаСкачать

Метода Гаусса: примеры решения СЛАУ
В данной статье мы:
- дадим определение методу Гаусса,
- разберем алгоритм действий при решении линейных уравнений, где количество уравнений совпадает c количеством неизвестных переменных, а определитель не равен нулю;
- разберем алгоритм действий при решении СЛАУ с прямоугольной или вырожденной матрицей.
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Метод Гаусса — что это такое?
Метод Гаусса — это метод, который применяется при решении систем линейных алгебраических уравнений и имеет следующие преимущества:
- отсутствует необходимость проверять систему уравнений на совместность;
- есть возможность решать системы уравнений, где:
- количество определителей совпадает с количеством неизвестных переменных;
- количество определителей не совпадает с количеством неизвестных переменных;
- определитель равен нулю.
- результат выдается при сравнительно небольшом количестве вычислительных операций.
Видео:Исследование систем линейных уравнений на совместностьСкачать

Основные определения и обозначения
Есть система из р линейных уравнений с n неизвестными ( p может быть равно n ):
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p ,
где x 1 , x 2 , . . . . , x n — неизвестные переменные, a i j , i = 1 , 2 . . . , p , j = 1 , 2 . . . , n — числа (действительные или комплексные), b 1 , b 2 , . . . , b n — свободные члены.
Если b 1 = b 2 = . . . = b n = 0 , то такую систему линейных уравнений называют однородной, если наоборот — неоднородной.
Решение СЛАУ — совокупность значения неизвестных переменных x 1 = a 1 , x 2 = a 2 , . . . , x n = a n , при которых все уравнения системы становятся тождественными друг другу.
Совместная СЛАУ — система, для которой существует хотя бы один вариант решения. В противном случае она называется несовместной.
Определенная СЛАУ — это такая система, которая имеет единственное решение. В случае, если решений больше одного, то такая система будет называться неопределенной.
Координатный вид записи:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p
Матричный вид записи: A X = B , где
A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n — основная матрица СЛАУ;
X = x 1 x 2 ⋮ x n — матрица-столбец неизвестных переменных;
B = b 1 b 2 ⋮ b n — матрица свободных членов.
Расширенная матрица — матрица, которая получается при добавлении в качестве ( n + 1 ) столбца матрицу-столбец свободных членов и имеет обозначение Т .
T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n
Вырожденная квадратная матрица А — матрица, определитель которой равняется нулю. Если определитель не равен нулю, то такая матрица, а потом называется невырожденной.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)
Для начала разберемся с определениями прямого и обратного ходов метода Гаусса.
Прямой ход Гаусса — процесс последовательного исключения неизвестных.
Обратный ход Гаусса — процесс последовательного нахождения неизвестных от последнего уравнения к первому.
Алгоритм метода Гаусса:
Решаем систему из n линейных уравнений с n неизвестными переменными:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + a 3 n x n = b 3 ⋯ a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n
Определитель матрицы не равен нулю.
- a 11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы;
- исключаем переменную x 1 из всех уравнений систему, начиная со второго;
- прибавим ко второму уравнению системы первое, которое умножено на — a 21 a 11 , прибавим к третьему уравнению первое умноженное на — a 21 a 11 и т.д.
После проведенных действий матрица примет вид:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n ,
где a i j ( 1 ) = a i j + a 1 j ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n , j = 2 , 3 , . . . , n , b i ( 1 ) = b i + b 1 ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n .
Далее производим аналогичные действия с выделенной частью системы:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n
Считается, что a 22 ( 1 ) не равна нулю. Таким образом, приступаем к исключению неизвестной переменной x 2 из всех уравнений, начиная с третьего:
- к третьему уравнению систему прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 ;
- к четвертому прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 и т.д.
После таких манипуляций СЛАУ имеет следующий вид:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( 2 ) n 3 x 3 + . . . + a ( 2 ) n n x n = b ( 2 ) n ,
где a i j ( 2 ) = a ( 1 ) i j + a 2 j ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n , j = 3 , 4 , . . . , n , b i ( 2 ) = b ( 1 ) i + b ( 1 ) 2 ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n . .
Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3 , действуя по аналоги с предыдущим образцом:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( n — 1 ) n n x n = b ( n — 1 ) n
После того как система приняла такой вид, можно начать обратный ход метода Гаусса:
- вычисляем x n из последнего уравнения как x n = b n ( n — 1 ) a n n ( n — 1 ) ;
- с помощью полученного x n находим x n — 1 из предпоследнего уравнения и т.д., находим x 1 из первого уравнения.
Найти решение системы уравнений методом Гаусса:
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4
Коэффициент a 11 отличен от нуля, поэтому приступаем к прямому ходу решения, т.е. к исключению переменной x 11 из всех уравнений системы, кроме первого. Для того, чтобы это сделать, прибавляем к левой и правой частям 2-го, 3-го и 4-го уравнений левую и правую часть первого, которая умножена на — a 21 a 11 :
— 1 3 , — а 31 а 11 = — — 2 3 = 2 3 и — а 41 а 11 = — 1 3 .
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = — 1 + ( — 1 3 ) ( — 2 ) — 2 x 1 — 2 x 2 — 3 x 3 + x 4 + 2 3 ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 9 + 2 3 ( — 2 ) x 1 + 5 x 2 — x 3 + 2 x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 4 + ( — 1 3 ) ( — 2 ) ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3
Мы исключили неизвестную переменную x 1 , теперь приступаем к исключению переменной x 2 :
— a 32 ( 1 ) a 22 ( 1 ) = — — 2 3 — 5 3 = — 2 5 и а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 + ( — 2 5 ) ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 23 3 + ( — 2 5 ) ( — 1 3 ) 13 3 x 2 — 4 3 x 3 + 5 3 x 4 + 13 5 ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 14 3 + 13 5 ( — 1 3 ) ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5
Для того чтобы завершить прямой ход метода Гаусса, необходимо исключить x 3 из последнего уравнения системы — а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 :
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5 ⇔
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 + 41 19 ( — 19 5 x 3 + 11 5 x 4 ) = 19 5 + 41 19 39 5 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19
Обратный ход метода Гаусса:
- из последнего уравнения имеем: x 4 = 392 19 56 19 = 7 ;
- из 3-го уравнения получаем: x 3 = — 5 19 ( 39 5 — 11 5 x 4 ) = — 5 19 ( 39 5 — 11 5 × 7 ) = 38 19 = 2 ;
- из 2-го: x 2 = — 3 5 ( — 1 3 — 11 3 x 4 + 4 3 x 4 ) = — 3 5 ( — 1 3 — 11 3 × 2 + 4 3 × 7 ) = — 1 ;
- из 1-го: x 1 = 1 3 ( — 2 — 2 x 2 — x 3 — x 4 ) = — 2 — 2 × ( — 1 ) — 2 — 7 3 = — 9 3 = — 3 .
Ответ: x 1 = — 3 ; x 2 = — 1 ; x 3 = 2 ; x 4 = 7
Найти решение этого же примера методом Гаусса в матричной форме записи:
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4
Расширенная матрица системы представлена в виде:
x 1 x 2 x 3 x 4 3 2 1 1 1 — 1 4 — 1 — 2 — 2 — 3 1 1 5 — 1 2 — 2 — 1 9 4
Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.
Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на — a 21 a 11 = — 1 3 , — a 31 a 11 = — — 2 3 = 2 3 и н а — а 41 а 11 = — 1 3 .
Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на — а 32 ( 1 ) а 22 ( 1 ) = — 2 3 — 5 3 = — 2 5 и — а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 — 7 3 5 3 | 23 3 0 13 3 — 4 3 5 3 | 14 3
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 + ( — 2 5 ) ( — 5 3 ) — 7 3 + ( — 2 5 ) 11 3 5 3 + ( — 2 5 ) ( — 4 3 ) | 23 3 + ( — 2 5 ) ( — 1 3 ) 0 13 3 + 13 5 ( — 5 3 ) — 4 3 + 13 5 × 11 3 5 3 + 13 5 ( — 4 3 ) | 14 3 + 13 5 ( — 1 3 )
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5
Теперь исключаем переменную x 3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 .
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 + 41 19 ( — 19 5 ) — 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
стала диагональной, т.е. приняла следующий вид:
x 1 x 2 x 3 x 4 3 0 0 0 | а 1 0 — 5 3 0 0 | а 2 0 0 — 19 5 0 | а 3 0 0 0 56 19 | 392 19 , где а 1 , а 2 , а 3 — некоторые числа.
Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на
— 11 5 56 19 = — 209 280 , н а — — 4 3 56 19 = 19 42 и н а — 1 56 19 = 19 56 .
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 1 + ( — 19 56 ) 56 19 | — 2 + ( — 19 56 ) 392 19 0 — 5 3 11 3 — 4 3 + 19 42 × 56 19 | — 1 3 + 19 42 × 392 19 0 0 — 19 5 11 5 + ( — 209 280 ) 56 19 | 39 5 + ( — 209 280 ) 392 19 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на
— 11 3 — 19 5 = 55 57 и н а — 1 — 19 5 = 5 19 .
x 1 x 2 x 3 x 4 3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 + 5 19 ( — 19 5 ) 0 | — 9 + 5 19 ( — 38 5 ) 0 — 5 3 11 3 + 55 57 ( — 19 5 ) 0 | 9 + 55 57 ( — 38 5 ) 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на — 2 — 5 3 = 6 5 .
x 1 x 2 x 3 x 4 3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 + 6 5 ( — 5 3 ) 0 0 | — 11 + 6 5 × 5 3 ) 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 0 0 0 | — 9 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
Полученная матрица соответствует системе уравнений
3 x 1 = — 9 — 5 3 x 2 = 5 3 — 19 5 x 3 = — 38 5 56 19 x 4 = 392 19 , откуда находим неизвестные переменные.
Ответ: x 1 = — 3 , x 2 = — 1 , x 3 = 2 , x 4 = 7 .
Видео:Теорема Кронекера-КапеллиСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы
Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.
Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.
В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание.
На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.
Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:
x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔
x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔
⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8
Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.
Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.
Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).
- В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
- Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
- Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.
📺 Видео
Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Базисные решения систем линейных уравнений (03)Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Неоднородная система линейных уравненийСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Лекция 12. Системы линейных уравненийСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Системы линейных уравнений: Теорема Кронекера-КапеллиСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение систем уравнений методом подстановкиСкачать







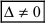 ), то система имеет единственное решение;
), то система имеет единственное решение;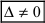 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 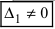 или
или 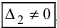 , или, . или
, или, . или 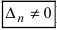 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);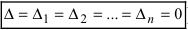 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.












