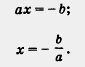Алгоритм построения графика уравнения ax by c 0

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Урок 85 График линейного уравнения ax + by = c с двумя переменными (7 класс)Скачать

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Видео:График линейного уравнения ax+by+c=0. 6 классСкачать

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Видео:График линейного уравнения с двумя переменными. 6 класс.Скачать

Линейное уравнение с двумя переменными и его график

График линейного уравнения с двумя переменными

В линейном уравнении с двумя переменными ax+by=c , a и b называют коэффициентами при переменных, c — свободным членом.

Если сравним полученное уравнение $с y = kx+ tilde b$ (см. §38 данного справочника), получаем:

Графиком $y = kx+ tilde b$ является прямая, угловой коэффициент k определяет угол наклона, слагаемое $tilde b$ – точку пересечения прямой с осью Y (см. §39 данного справочника).

Точки пересечения с осями координат:

График линейной функции ax+by=c с ненулевыми коэффициентами очень удобно чертить по двум точкам пересечения с осями координат: точка на оси X ( $frac$;0) и точка на оси Y (0; $frac$)

Равенство нулю коэффициентов при переменных:

$0x+2y = 4 Rightarrow y = 2$

График – прямая, параллельная оси Х.

$3x+0y = 3 Rightarrow x = 1$

График – прямая, параллельная оси У.

a = 0, b = 0, $c neq 0$

x, $y in Bbb R$ — любое действительное число.

График – вся координатная плоскость

График – пустое множество.

Взаимное расположение графиков двух уравнений

$$ a_1 x+b_1 y = c_1 и a_2 x+b_2 y = c_2 $$

Видео:8 класс, 20 урок, Функция y=ax^2+bx+c, ее свойства и графикСкачать

Алгоритм построения графика уравнения ax by c 0

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Линейное уравнение с двумя переменными и его график

Нам часто встречались уравнения вида ах + b = 0, где а, b — числа, х — переменная. Например, bх — 8 = 0, х + 4 = О, — 7х — 11 = 0 и т. д. Числа а, Ь (коэффициенты уравнения) могут быть любыми, исключает лишь случай, когда а = 0.

Уравнение ах + b = 0, где а 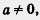, называют линейным уравнением с одной переменной х (или линейным уравнением с одним неизвестным х). Решить его, т. е. выразить х через а и b, мы с вами умеем:

Ранее мы отмечали, что довольно часто математической моделью реальной ситуации служит линейное уравнение с одной переменной или уравнение, которое после преобразований сводится к линейному. А теперь рассмотрим такую реальную ситуацию.

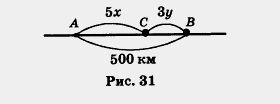
Из городов A и В, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3 ч после выхода второго поезда они встретились. Чему равны скорости поездов?

Составим математическую модель задачи. Пусть х км/ч — скорость первого поезда, у км/ч — скорость второго поезда. Первый был в пути 5 ч и, значит, прошел путь bх км. Второй поезд был в пути 3 ч, т.е. прошел путь Зу км.

Их встреча произошла в пункте С. На рисунке 31 представлена геометрическая модель ситуации. На алгебраическом языке ее можно описать так:

или
5х + Зу — 500 = 0.

Эту математическую модель называют линейным уравнением с двумя переменными х, у.
Вообще,

где а, b, с — числа, причем 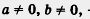, — линейное уравнение с двумя переменными х и у (или с двумя неизвестными х и у).

Вернемся к уравнению 5х + Зу = 500. Замечаем, что если х = 40, у = 100, то 5 • 40 + 3 • 100 = 500 — верное равенство. Значит, ответ на вопрос задачи может быть таким: скорость первого поезда 40 км/ч, скорость второго поезда 100 км/ч. Пару чисел х = 40, у = 100 называют решением уравнения 5х + Зу = 500. Говорят также, что эта пара значений (х; у) удовлетворяет уравнению 5х + Зу = 500.

К сожалению, это решение не единственно (мы ведь все любим определенность, однозначность). В самом деле, возможен и такой вариант: х = 64, у = 60; действительно, 5 • 64 + 3 • 60 = 500 — верное равенство. И такой: х = 70, у = 50 (поскольку 5 • 70 + 3 • 50 = 500 — верное равенство).

А вот, скажем, пара чисел х = 80, у = 60 решением уравнения не является, поскольку при этих значениях верного равенства не получается:

Вообще, решением уравнения ах + by + с = 0 называют всякую пару чисел (х; у), которая удовлетворяет этому уравнению, т. е. обращает равенство с переменными ах + by + с = 0 в верное числовое равенство. Таких решений бесконечно много.

Замечание. Вернемся еще раз к уравнению 5х + Зу = 500, полученному в рассмотренной выше задаче. Среди бесконечного множества его решений имеются, например, и такие: х = 100, у = 0 (в самом деле, 5 • 100 + 3 • 0 = 500 — верное числовое равенство); х = 118, у = — 30 (так как 5 • 118 + 3 • (-30) = 500 — верное числовое равенство). Однако, являясь решениями уравнения, эти пары не могут служить решениями данной задачи, ведь скорость поезда не может быть равной нулю (тогда он не едет, а стоит на месте); тем более скорость поезда не может быть отрицательной (тогда он едет не навстречу другому поезду, как сказано в условии задачи, а в противоположную сторону).

Пример 1. Изобразить решения линейного уравнения с двумя переменными х + у — 3 = 0 точками в координатной плоскости хОу.

Решение. Подберем несколько решений заданного уравнения, т. е. несколько пар чисел, которые удовлетворяют уравнению: (3; 0), (2; 1), (1; 2) (0; 3), (- 2; 5).

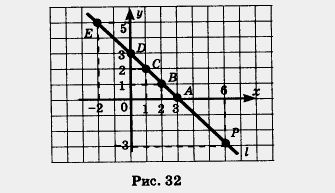
Построим в координатной плоскости хОу точки А (3; 0), B(2; 1), С (1; 2), D (0; 3), Е (- 2; 5) (рис. 32). Обратите внимание: все эти пять точек лежат на одной прямой I, проведем ее.

Говорят, что прямая I является графиком уравнения х + у — 3 = 0. Говорят также, что прямая I — геометрическая модель уравнения х + у — 3 = 0

Итак, если пара чисел (х; у) удовлетворяет уравнению х + у — 3 = 0, то точка М (х; у) принадлежит прямой I; если точка М(х; у) принадлежит прямой I, то пара (х; у) — решение уравнения х + у — 3 = 0. Например, точка Р(6; -3) принадлежит прямой I (рис. 32) и пара (6; -3) — решение уравнения х + у-3 = 0

Доказать теорему нам с вами пока не под силу — это будет сделано позднее, в курсе геометрии. Но пользоваться теоремой мы, конечно, имеем право уже сейчас.

Кстати, догадываетесь ли вы, откуда появился термин «линейное уравнение»? Это фактически напоминание о геометрической модели — прямой линии, которая служит график уравнения.

Пример 2. Построить график уравнения Зх-2у+6=0.

Решение. Подберем несколько решений заданного уравнения:

1) (0; 3); в самом деле, если х = 0, у = 3, то 3 • 0-2 • 3 + 6 = 0 — верное равенство (в уравнение Зx — 2у + 6 = 0 мы подставили значения х = 0, у = 3);

2) (- 2; 0); действительно, если х = — 2, у = 0, то 3 • (-2)-2 • 0 + 6 = 0 — верное равенство;

3) (2; 6); если х = 2, у = 6, то 3 • 2-2 • 6 + 6 = 0 — верное равенство;

4) (4; 9); если х = 4, у = 9, то 3 • 4-2 • 9 + 6 = 0 — верное равенство.

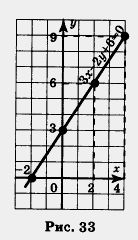
Построим точки (3; 3), (- 2; 0), (2; 6), (4; 9) на координатной плоскости хОу. Они лежат на одной прямой, проведем ее (рис. 33). Эта прямая и Рис. 33 есть график уравнения Зx — 2у + 6 = 0.

Пример решен, хотя и верно, но очень нерационально. Почему? Давайте рассуждать.

1. Мы знаем, что графиком линейного уравнения Зx — 2у + 6 = 0 является прямая (это утверждается в теореме). Чтобы провести прямую, достаточно указать две ее точки. Через две точки можно провести прямую и притом только одну — этому нас учит геометрия. Поэтому построенные выше четыре точки — это явный перебор. Достаточно было построить точки (0; 3) и (-2; 0) и с помощью линейки провести через них прямую.

2. Решения данного уравнения мы подбирали, т.е. угадывали. Угадать что-либо всегда труднее, чем действовать по определенному правилу. Нельзя ли было и здесь не угадывать, а действовать по какому-то правилу? Можно. Например, так. Дадим переменной х конкретное значение, например х = 0 (обычно пишут х₁ = 0). Подставив это значение в уравнение Зx — 2у + 6 = 0, получим: 3 • 0 — 2у + 6 = 0, т.е. -2у + 6 = 0. Из этого уравнения находим: у = 3 (обычно пишут у₁ = 3). Значит, если х = 0, то у = 3; пара (0; 3) — решение данного уравнения.

Дадим переменной х еще одно конкретное значение, например х = — 2 (обычно пишут хг = — 2). Подставив это значение в уравнение Зх-2у + 6 = 0, получим: 3 • (-2) — 2у + 6 = 0, т. е. — 2у = 0. Из этого уравнения находим у = 0 (обычно пишут у2 = 0). Значит, если х = -2, то у = 0; пара (- 2; 0) — решение данного уравнения.

Вот теперь мы в состоянии сформулировать алгоритм построения графика линейного уравнения ах + by + с = 0 (где, напомним, а,b,с — любые числа,

Алгоритм построения графика уравнения
ах + by + с = 0

Замечание. Чаще всего на первом шаге алгоритма берут значение х = 0. Второй шаг иногда немного изменяют: полагают у = 0 и находят соответствующее значение х.

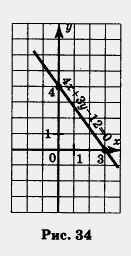
Пример 3. Построить график уравнения

Решение. Будем действовать по алгоритму (с учетом замечания).

1) Положим х = 0, подставим это значение в уравнение 4х + Зу- 12 = 0, получим: 4 • 0 + Зу -12 = 0, Зу-12 = 0, у = 4.

2) Положим у = 0, подставим это значение в уравнение 4х + Зу — 12 = 0, получим: 4 • х + 3 • 0 — 12 — 0, 4х — 12 = 0, х = 3.

3) Построим на координатной плоскости хОу две точки: (0; 4) — она найдена на первом шаге алгоритма и (3; 0) — она найдена на втором шаге.

4) Проведем через точки (0; 4) и (3; 0) прямую. Это и есть искомый график (рис. 34).

Пример 4. Иванов и Петров посадили на своих садовых участках яблони, причем Петров посадил яблонь в 2,5 раза больше, чем Иванов. На следующий год они увеличили число яблонь (подсадили новые саженцы), причем у Иванова стало яблонь в 3 раза больше, чем было, а у Петрова в 2 раза больше, чем было. В итоге у них вместе стало 16 яблонь. Сколько яблонь посадили Иванов и Петров в первый год?

Первый этап. Составление математической модели. Пусть х — число яблонь, посаженных в первый год Ивановым, а у — число яблонь, посаженных в первый год Петровым. По условию задачи у = 2,5х. Здесь целесообразно умножить обе части уравнения на 2, получим: 2у = 5х. Это уравнение перепишем в виде:

Далее, на второй год Иванов увеличил число саженцев на своем участке в 3 раза и, значит, у него стало Зx яблонь. Петров увеличил число саженцев на своем участке в 2 раза, т. е. у него стало 2у яблонь. По условию у обоих в сумме стало 16 яблонь, т. е. Зх + 2у= 16. Перепишем это уравнение в виде

3x + 2у — 16 = 0. (2)

Математическая модель задачи готова, она состоит из двух линейных уравнений с двумя переменными хну — из уравнений (1) и (2). Обычно в таких случаях уравнения записывают одно под другим и используют специальный символ — фигурную скобку:

Второй этап. Работа с составленной моделью. Интересующая нас пара чисел (х; у) должна удовлетворять и уравнению (1), и уравнению (2), т. е. интересующая нас точка (х; у) должна лежать как на прямой (1), так и на прямой (2). Что делать?

Ответ очевиден: надо построить прямую (1), затем прямую (2) и, наконец, найти точку пересечения этих прямых.

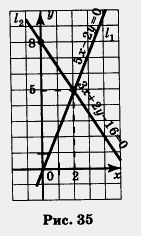
1) строим график уравнения Ьх — 2у = 0. Если х = 0, то у = 0; если х = 2, то у = 5. Проведем через точки (0; 0) и (2; 5) прямую I₁ (рис. 35).

2) строим график уравнения Зx + 2у — 16 = 0. Если х = 0, то у = 8; если х = 2, то у = 5. Проведем через точки (0; 8) и (2; 5) прямую 12 (см. 35).

3) прямые I₁ и I₂ пересекаются в точке (2; 5), т. е. х = 2, у = 5.

Третий этап. Ответ на вопрос задачи.

Спрашивается, сколько яблонь посадили в первый год Иванов и Петров, т. е. чему равны хну? Ответ на этот вопрос уже получен: х — 2, у = 5.

О т в е т: в первый год Иванов посадил 2 яблони, а Петров — 5 яблонь.

Как видите, не зря мы с вами учились строить графики линейных уравнений с двумя переменными. Это позволило нам от одной математической модели (алгебраической модели (3)) перейти к другой математической модели — геометрической (две прямые на координатной плоскости на рисунке 35), что и дало возможность довести решение до конца.

А можно ли работать непосредственно смоделью (3), не переходя к геометрической модели?

Можно, но об этом речь впереди, в главе 8. Там, используя новые знания, мы снова вернемся к модели (3).

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

💡 Видео

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Алгебра 7класс Тема 25. График линейного уравнения ax + by = c с двумя переменнымиСкачать

ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

График линейного уравнения с двумя переменными, 7 классСкачать

Как построить график линейной функции.Скачать

Как построить график функции без таблицыСкачать

Занятие 1. График линейной функции y=kx+bСкачать

График линейного уравнения с двумя переменными ax+by=cСкачать

АЛГЕБРА 8 класс: Квадратичная функция y = ax^2 + bx + c , её свойства и график | ВидеоурокСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать