Этот метод исключительно удобен для использования на ЭВМ.
Рассмотрим систему из трех уравнений с тремя неизвестными:
Предположим, что аиФ 0; аи Ф 0; а33 Ф 0, и перепишем систему в следующем виде:
Теперь возьмем некоторое первое приближение к решению этой системы, обозначив его через х, (0) , х2 х* 01 . Подставим это решение в (3.18) и вычислим новое значение х, (1) :
Используя только что вычисленное значение х<'* и начальное значение * 0) = 0, х ( 2 >] = 0, х = 0, как это обычно делается для начального приближения. Тогда, согласно формулам:
Получаем следующее приближение:
Последовательные приближения, вычисленные каждый раз с точностью до четырех значащих цифр, приведены в табл. 3.1.
Для системы из п уравнений с п неизвестными (диагональные элементы отличны от нуля) к-е приближение к решению будет задаваться функцией
Интерполяционный процесс продолжается до тех пор, пока все х- к) не станут достаточно близки к х^
г> . Критерий близости можно задавать в следующем виде:
где определяется максимальное значение разности для всех /, a s — некоторое положительное число.
Достаточным условием сходимости метода Гаусса-Зейделя является то, что диагональные члены должны преобладать в уравнении, т. е. они должны быть по абсолютной величине не меньше, а по крайней мере в одном случае больше недиагональных элементов для всех или для одного /:
Блок-схема алгоритма решения системы линейных уравнений итерационным методом Гаусса-Зейделя представлена на рис. 3.2, программа расчета на языке Паскаль приведена в приложении.
В качестве практического примера использования методов решения систем линейных уравнений приведем поиск коэффициентов параболической аппроксимации по набору экспериментальных точек (см. пример 5.8 раздела 5.3.3). Решение этого примера надежнее проводить с помощью прямого метода Гаусса, т. к. условие сходимости итерационного метода Гаусса-Зейделя может не выполниться. Блок-схема алгоритма расчета представлена на рис. 3.3. Программа расчета на языке Паскаль приведена в приложении. Матрица коэффициентов системы линейных уравнений обозначена двумерным массивом аа, искомые коэффициенты параболической аппроксимации — массивом а.
Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Вопросы для самоконтроля
- 1. В чем состоит постановка задачи при решении систем линейных уравнений?
- 2. Какие знаете методы решения линейных уравнений?
- 3. На чем основано решение систем линейных уравнений методом Гаусса?
- 4. Сущность метода Гаусса-Зейделя?
Рис. 3.2. Блок-схема решения системы линейных уравнений методом Гаусса-Зейделя

Рис. 3.3. Блок-схема расчета коэффициентов квадратичной аппроксимации зависимости теплоемкости циклопропана от температуры с использованием метода Гаусса
Видео:6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

РАЗРАБОТКА ТЕХНИЧЕСКИХ ТРЕБОВАНИЙ И ПОСТАНОВКА ЗАДАЧ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ
Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Зейделя. Блок-схема алгоритма решения системы линейных уравнений методом Зейделя представлена на рисунке 2. В качестве исходных данных вводятся коэффициенты и правые части уравнений системы, погрешность , допустимое число итераций М, а так же начальные приближения переменных . Отметим, что начальные приближения можно не вводить в ЭВМ, а полагать их равными некоторым значениям (например нулю) [5].
Для удобства чтения блок-схемы объясним некоторые обозначения: k — порядковый номер итерации; i — номер уравнения, а так же переменного, которое вычисляется в данном цикле; j — номер члена вида . Итерации прекращаются либо после выполнения условия
либо при k=M. В последнем случае итерации не сходятся, и после М итераций счет прекращается без выдачи результатов. Можно предусмотреть в этом случае также и вывод на печать некоторой поясняющей информации.
Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной учитываются уже вычисленные ранее (k+1)-е приближения .
Пусть дана приведенная линейная система:
Выберем произвольно начальные приближения корней
стараясь, конечно, чтобы они в какой-то мере соответствовали неизвестным
Далее предполагая, что k-е приближение корней известно, тогда в соответствии с идеей метода будем строить (k+1) — е приближение по следующим формулам:
Рисунок 2.1 Блок-схема метода Зейделя

Обычно процесс Зейделя дает лучшую сходимость, чем метод простой итерации, но, вообще говоря, он приводит к более громоздким вычислениям. Процесс Зейделя может сходится даже в том случае, если расходится процесс итерации. Однако это бывает не всегда. Возможны случаи, когда процесс Зейделя сходится медленнее процесса итерации. Более того, могут быть случаи, когда процесс итерации сходится, а процесс Зейделя расходится.
Пример. Методом Зейделя решить систему уравнений
Решение. Приведем эту систему к виду, удобному для итерации,
В качестве нулевых приближений корней возьмем:
Применяя процесс Зейделя, последовательно получим:
Результаты вычислений с точностью до четырех знаков поместим в таблицу 2.1.
Таблица 2.1 Результаты вычислений
|
|
|
|
Точные значения корней: ; ; .
Случай нормальной системы [3].
Определение. Целый однородный полином второй степени от n переменных называется квадратичной формой этих переменных. В общем случае квадратичная форма имеет вид
где -постоянные числа, причем для удобства соответствующие коэффициенты при взяты взяты в четной форме . Приравняв t постоянной с, получим уравнение центральной поверхности второго порядка
в n-мерном пространстве.
т.е. , то формулу (2.1) короче можно записать следующим образом:
носит название матрицы квадратичной формы (2.1′). В силу условия (2.3) матрица А будет симметрической, т.е. совпадет со своей транспонированной матрицей. Наоборот, для всякой симметрической матрицы можно построить соответствующую квадратичную форму (2.1′).
Определение. Квадратичная форма (2.3) называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения, обращаясь в нуль лишь при .
Если -положительно определенная квадратичная форма, то уравнение
представляет собой уравнение эллипсоида. Заметим, что в случае
Определение. Назовем линейную систему
нормальной, если: 1) матрица коэффициентов -симметрическая, т.е. , 2) соответствующая квадратичная форма
Нормальные системы встречаются при решении многих вопросов, например, в способе наименьших квадратов, при нахождении направлений главных осей эллипсоида и т.д. Нормальную систему (2.4) приведем обычным способом к специальному виду
Теорема. Если линейная система (2.4)-нормальная, то процесс Зейделя для эквивалентной ей приведенной системы (2.4′) всегда сходится.
Доказательство. Пусть линейная система
— нормальная, т.е. матрица — симметрическая и положительно определенная. Положим
— диагональная, — нижняя треугольная,
верхняя треугольная матрица, являющаяся ввиду симметричности матрицы транспонированной по отношению к матрице . Тогда имеем:
Согласно предыдущему процесс Зейделя для системы (2.5) или эквивалентной ей системы (3.6) строится следующим образом:
Для сходимости процесса необходимо и достаточно, чтобы все собственные значения матрицы
были по модулю меньше единицы.
В нашем случае имеем:
Пусть -единичный собственный вектор матрицы М, соответствующий собственному значению , т.е.
( и действительны и ).
Ввиду того, что матрица является транспонированной по отношению к матрице , получаем:
Используя положительную определенность матрицы А, будем иметь:
Далее, учитывая положительность числа , очевидно, имеем:
Таким образом, всегда выполнено неравенство
Отсюда для членов дроби (2.8) будем иметь:
Способ приведения линейной системы к нормальному виду указывается следующей теоремой [4]
Теорема. Если обе части линейной системы
с неособенной матрицей умножить слева на транспортированную матрицу , то полученная новая система
зейдель программирование mathcad алгоритм
Доказательство. Докажем сначала, что матрица есть симметрическая матрица. В самом деле, имеем:
Теперь докажем, что квадратичная, соответствующая матрице ,-положительно определенная. Составим квадратичную форму с матрицей :
Изменяя порядок суммирования, получим:
Так как значение суммы не зависит от обозначения индекса суммирования, то
Поэтому однородная система
имеет лишь нулевые решения. Следовательно,
Необходимые и достаточные условия сходимости процесса Зейделя для системы линейных уравнений [3].
Для линейной системы
рассмотрим процесс Зейделя
при произвольном начальном векторе
Тогда процесс Зейделя в матричном виде можно записать следующим образом:
Теорема. Для сходимости процесса Зейделя (2.14) для системы (2.13) при любом выборе свободного члена и начального вектора необходимо и достаточно, что бы все корни уравнения
были по модулю меньше единицы.
Доказательство. Из формулы (2.14) вытекает:
Матрица -неособенная, так как
Поэтому равенство (2.16) можно записать в виде
Отсюда ясно, что процесс Зейделя эквивалентен процессу итерации, примененному к линейной системе
Для сходимости итерационного процесса (2.17) необходимо и достаточно, чтобы корни характеристического уравнения
Уравнение (2.18), очевидно, равносильно уравнению (2.15).
Для применения метода Зейделя систему (2.19) обычно записывают в форме
Причем треугольные матрицы В и С реализуют разбиение матрицы системы (2.20), необходимое для применения процесса Зейделя. На основании формулы (2.15) сходимость процесса Зейделя для системы (2.19) зависит от свойств корней уравнения
Уравнение (2.21) можно заменить эквивалентным уравнением
Таким образом, для сходимости процесса Зейделя для системы (2.19) при любом свободном члене и любом начальном приближении необходимо и достаточно, чтобы все корни уравнения (2.22) удовлетворяли условиям
Области сходимости процесса обычной итерации и процесса Зейделя, вообще говоря, перекрываются. Можно привести примеры линейных систем, для которых процесс обычной итерации сходится, а процесс Зейделя расходится, и обратно.
Рассмотрим линейную систему
с кососимметрической матрицей
Характеристическое уравнение матрицы имеет вид
Для сходимости метода обычной итерации необходимо и достаточно, чтобы
(область А на рисунке 3).
Для метода Зейделя уравнение, определяющее сходимость, имеет вид
Для того что бы корни и уравнения (2.24) удовлетворяли условиям
необходимо и достаточно выполнение неравенств
Так как область А и В частично перекрываются, то отсюда следует, что для системы (2.23) можно выбрать коэффициенты и , во-первых, так, чтобы метод итерации сходился, а метод Зейделя расходился (например ; ), и, во-вторых, так, чтобы, наоборот, метод Зейделя сходился, а метод итерации расходился (например, ; ).
Рисунок 2.1 Области сходимости метода простой итерации и метода Зейделя
Видео:Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

1.2.3. Метод Зейделя (метод Гаусса-Зейделя, метод последовательных замещений)
Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения неизвестных x1, х2, .
В этом методе, как и в методе простой итерации, необходимо привести систему к виду (3), чтобы диагональные коэффициенты были максимальными по модулю, и проверить условия сходимости. Если условия сходимости не выполняются, то нужно произвести элементарные преобразования (см. п. 4). Пусть дана система из трех линейных уравнений. Приведем ее к виду (3). Выберем произвольно начальные приближения корней: х1(0), х2(0), х3(0), стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным. За нулевое приближение можно принять столбец свободных членов, т. е. х(0) = b
(т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3). Найдем Первое приближение х(1) по формулам:
Следует обратить внимание на особенность метода Зейделя, которая состоит в том, что полученное в первом уравнении значение х1(l) сразу же используется во втором уравнении, а значения х1(1), х2(1) – в третьем уравнении и т. д. То есть все найденные значения х1(1) подставляются в уравнения для нахождения хi+1(1) [6, 8].
Рабочие формулы для метода Зейделя для системы трех уравнений имеют следующий вид:
Запишем в общем виде для системы n-уравнений рабочие формулы:
Заметим, что теорема сходимости для метода простой итерации справедлива и для метода Зейделя.
Зададим определенную точность решения e, по достижении которой итерационный процесс завершается, т. е. решение продолжается до тех пор, пока не будет выполнено условие для всех уравнений: 
Пример №2. Методом Зейделя решить систему с точностью e = 10-3:
1. Приведем систему к виду:
2. В качестве начального вектора х(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:
3. Проведем итерации методом Зейделя. При k = 1

При вычислении х2(1) используем уже полученное значение х1(1) =
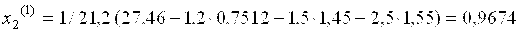
При вычислении х3(1) используем значения х1(1) и х2(1):
Наконец, используя значения х1(1), х2(1), х3(1), получаем:
Аналогичным образом ведем вычисления при k=2 и k=3. При k= 2:
Найдем модули разностей значений 
Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,80006, x2 = 1,00002, x3 = 1,19999, x4 = 1,40000.
💡 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Метод Зейделя Пример РешенияСкачать

9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод простой итерации Пример РешенияСкачать

Решение системы уравнений методом ГауссаСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

3 Метод простой итерации Блок-схема Решение системы линейных уравнений СЛАУСкачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Матричный метод решения систем уравненийСкачать

Решение системы уравнений методом Гаусса 4x4Скачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод_Зейделя_ExcelСкачать

Решение систем линейных алгебраических уравнений методом Зейделя (устар.)Скачать

ФСР системы линейных уравнений. Алгоритм ГауссаСкачать









































































