2. 5. Комбинированный метод хорд и касательных
Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, тогда уточнение корня происходит быстрее.
Пусть дано уравнение f ( x ) = 0, корень отделен на отрезке [ a , b ].
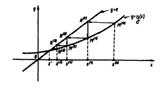
Рассмотрим случай, когда f ‘( x ) f ’’( x )>0 (рис. 2.13).
В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b ).
Тогда вычисления следует проводить по формулам:
Теперь корень ξ заключен в интервале [ a 1, b 1]. Применяя к этому отрезку комбинированный метод, получим:
Если же f ‘( x ) f ’’( x )
Вычислительный процесс прекращается, как только выполнится условие:
Видео:Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Электронная библиотека
Метод Ньютона называют также методом касательных. Комбинируя метод хорд и метод Ньютона, можно построить метод отыскания вещественных корней уравнения f(x) = 0, в котором при прежних предположениях относительно f(x) на каждом шаге итерационного процесса мы получаем два приближения к корню и , причем где с –точное значение корня.
1. Условия на применение метода те же, что и в методе Ньютона.
Пусть известен отрезок [a, b], который содержит один корень уравнения: f(x) = 0. Функция f(x) является дважды непрерывно дифференцируемой на [a, b] (f(x) Î C 2 [a, b]). Функция f принимает на концах отрезка [a, b] значения разных знаков (f(a)×f(b) 0, то слева применяем метод Ньютона, а справа метод хорд.
· если f(b)×f ¢¢(x) > 0, то слева применяем метод хорд, а справа метод Ньютона (метод касательных).
В качестве точек начального приближения выбираются: x0 = a, .
4. Условие остановки итерационного процесса: , при выполнении этого условия любая точка из отрезка [ ] приближает корень уравнения с точностью e.
Чаще всего принимают: .
На рис. 2.8. иллюстрируется применение комбинированного метода хорд и касательных. В рассматриваемом случае справа применяется метод Ньютона, а слева – метод хорд.
Рис. 2.8. Геометрический смысл комбинированного метода хорд и касательных
Построить алгоритм для уточнения корня уравнения x 3 + 3x – 1 = 0 комбинированным методом хорд и касательных с точностью e на отрезке [0.1, 1].
1. В предыдущих примерах мы проверили, что отрезок [0.1, 1] содержит один корень уравнения, и выполняются все условия для применения метода Ньютона:
2. Определим, какой из методов нужно применять слева, а какой справа:
Следовательно, слева применяем метод хорд, а справа – метод касательных (Ньютона). Запишем формулы:
3. Точки начального приближения:
4. Условие остановки итерационного процесса:
При выполнении условия остановки итерационного процесса х* является приближенным значением корня уравнения, полученным комбинированным методом хорд и касательных с точностью e.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Численное решение нелинейного уравнения. Этапы решения.
f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.
Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.
Задача нахождения корней состоит из 2 этапов:
1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:
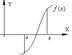
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.
Классификация методов уточнения корней :
1) Метод половинного деления отрезка(дихотомии).

Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.

Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).

В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.
Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).
4) Комбинированный метод – объединение методов хорд и касательных.

Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).
5) Метод простой итерации.
Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.
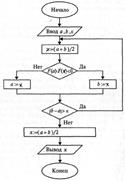
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм. Требуется вычислить корень уравнения f(x)=0 на [a;b] с заданной погрешностью Е. Отрезок [a;b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е.  Алгоритм метода: Алгоритм метода: |




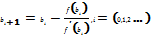
🎦 Видео
Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Метод половинного деления решение нелинейного уравненияСкачать

Численное решение уравнений, урок 1/5. Локализация корняСкачать
Метод простых итераций пример решения нелинейных уравненийСкачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод половинного деления. ДихотомияСкачать

Метод хордСкачать

Метод касательных (метод Ньютона)Скачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

10 Численные методы решения нелинейных уравненийСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод Ньютона, или Извлечение квадратного корняСкачать

1,2 Решение нелинейных уравнений методом хордСкачать