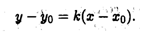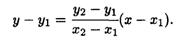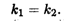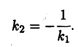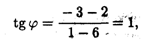Алгебраической линией 1 го порядка на плоскости является линия с уравнением (4 видео)

Содержание

3.1. Алгебраическая линия и её порядок
03.9.2. Линии первого порядка
Алгебраические уравнения линий на плоскости
Теорема (3.1) об инвариантности порядка алгебраической линии
🔍 Видео

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

3.1. Алгебраическая линия и её порядок

И сразу разбираемся в терминах:

Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид , где – многочлен, состоящий из слагаемых вида , где – действительное число, – целые неотрицательные числа.

Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательных степенях (т.е. корней и переменных в знаменателе тоже нет).

Порядок линии равен максимальному значению входящих в него слагаемых . Так, в уравнении прямой :

– слагаемое содержит «икс» в 1-й степени;
– слагаемое содержит «игрек» в 1-й степени;
– в слагаемом переменные отсутствуют, поэтому сумма их степеней равна нулю.

Максимальное значение равно 1, и поэтому прямая – это линия первого порядка.

Общее уравнение линии второго порядка имеет вид:
, где – произвольные действительные числа ( принято записывать с множителем-«двойкой»), причём коэффициенты не равны одновременно нулю.

Почему порядок этой линии равен двум?

– слагаемое содержит «икс» во 2-й степени;
– у слагаемого сумма степеней равна: 1 + 1 = 2;
– слагаемое содержит «игрек» во 2-й степени;
– все остальные слагаемые – меньшей степени.

Максимальное значение 2, и поэтому порядок линии равен двум.

Если к этому уравнению дополнительно приплюсовать, скажем, , то оно уже будет определять линию третьего порядка. Очевидно, что общее уравнение линии третьего порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
, где коэффициенты не равны одновременно нулю.

В том случае, если добавить одно или несколько слагаемых, которые содержат , то речь уже зайдёт о линии четвёртого порядка, и так далее.

С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат. Ну а пока осваиваем порядок второй. Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости, и для простоты будем считать, что все события происходят в декартовой системе координат .

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

03.9.2. Линии первого порядка

К линиям первого порядка относятся те линии, для которых задающее их уравнение (3.9) содержит переменные X и у только в первой степени. Иными словами, такие линии описываются уравнениями вида

Где А, В и С — постоянные числа. Из этого уравнения можно выразить переменную У как функцию от аргумента Х При В ≠ 0:

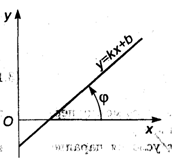
Уравнение (3.11) называют Уравнением прямой с угловым коэффициентом K = tg φ, где φ — угол наклона прямой к положительному направлению оси Ох (рис. 3.9). Если K = 0, то прямая параллельна оси Ох и отстоит от нее на B масштабных единиц.

Определим самые необходимые элементы знания о прямых на плоскости.

1. Кроме «классического» уравнения прямой (3.11) следует знать еще две его разновидности. Первая из них — это уравнение прямой с заданным угловым коэффициентом K, проходящей через заданную точку М0(X0, У0):

Другой вид — это уравнение прямой, проходящей через две заданные точки на плоскости M1(X1, Y1) и М2(х2, у2):

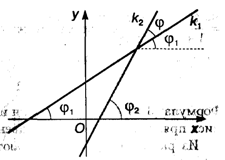
2. Угол между прямыми. Рассмотрим две прямые, заданные уравнениями У = K1X + B1 и У = K2X + B2, где K1 = tg φ1 И K2 = tg φ2 (рис. 3.10). Пусть φ — угол между этими прямыми. Тогда φ = φ2 — φ1 и мы получаем tg φ = tg (φ2 — φ1) = 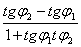Или, что то же самое,

Формула (3.12) определяет один из углов между пересекающимися прямыми; второй угол равен π — φ.

Из равенства (3.12) вытекают условия параллельности и перпендикулярности прямых. В самом деле, если прямые параллельны, то

Если прямые перпендикулярны, то α2 = π/2 + α1, откуда tg α2 = — ctg α1 = -1 / tg α1, или окончательно

Пример 1. Найти угол между прямыми, заданными уравнениями У = 2X — 5 и У = -3X + 4.

Решение. Подставляя в формулу (3.12) значения K1 = 2 и K2 = -3, имеем

Откуда получаем, что один из углов равен φ = π / 4.

3. Расстояние от точки до прямой. Пусть прямая задана уравнением общего вида (3.10). Тогда расстояние D От произвольной точки М0(X0, Y0) до прямой (рис. 3.11) дается формулой

Видео:9 класс, 5 урок, Уравнение линии на плоскостиСкачать

Алгебраические уравнения линий на плоскости

Напомним, что многочленом степени одной переменной называется выражение вида

где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .

Многочленом двух переменных называется выражение вида

где — действительные числа (коэффициенты многочлена), и — целые неотрицательные числа. Число

называется степенью многочлена двух переменных.

Алгебраической линией на плоскости называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида

где — многочлен двух переменных и .

Уравнение вида (3.4) называется алгебраическим уравнением с двумя неизвестными. Степенью уравнения (3.4) называется степень многочлена . Одна и та же линия может быть задана уравнением вида (3.4) с многочленами разных степеней. Порядком алгебраической линии называется наименьшая из степеней этих многочленов.

Всякую неалгебраическую линию называют трансцендентной.

В примере 3.1,а,б,в,г,е — линии алгебраические: а — первого порядка, б,в,г,е — второго порядка. Примером трансцендентной линии служит синусоида, т.е. график функции . Эту линию нельзя задать уравнением вида (3.4).

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Теорема (3.1) об инвариантности порядка алгебраической линии

Если в некоторой аффинной системе координат на плоскости линия задана уравнением (3.4), то и в любой другой аффинной системе координат эта линия задается уравнением того же вида (3.4) и той оке степени.

Действительно, пусть в аффинной системе координат уравнение имеет вид (3.4):

Получим уравнение этой линии в другой (новой) аффинной системе координат . Старые координаты точки связаны с новыми ее координатами выражениями (2.8):

где — координаты вектора переноса начала координат , а — элементы матрицы перехода базиса к новому . Подставим эти выражения в одночлен :

Раскрывая скобки, получаем многочлен двух переменных , степень которого не больше, чем . Аналогичные многочлены получим из других одночленов, входящих в левую часть (3.4). Сложив эти многочлены, получим многочлен , степень которого не превосходит степени исходного многочлена . Таким образом, при замене системы координат порядок алгебраической линии не увеличивается. Но он не может и уменьшиться, так как если порядок уменьшится при переходе к новой системе координат, то он должен увеличиться при обратном переходе к старой системе координат. Следовательно, порядок алгебраической линии остается неизменным в любой аффинной системе координат (говорят, что порядок алгебраической линии является инвариантом). Теорема доказана.

В аналитической геометрии на плоскости изучаются:

– алгебраические линии первого порядка, описываемые алгебраическим уравнением первой степени с двумя неизвестными:

– алгебраические линии второго порядка, описываемые алгебраическим уравнением второй степени с двумя неизвестными:

1. Теорема 3.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных

где , степень многочлена не изменяется.

Действительно, преобразование уравнения при переходе от одной системы координат к другой соответствует линейной невырожденной замене переменных многочлена в левой части уравнения.

2. Алгебраическое уравнение (3.4) может не иметь действительных решений. Например, на плоскости нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теоремы алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (3.4) , где и , задает некоторую алгебраическую линию на двумерной комплексной плоскости (см. пункт 2 замечаний 2.9). Если все точки этой линии вещественные (действительные), т.е. , а , то линию называют вещественной (действительной). В противном случае линию называют мнимой.

3. Алгебраическими неравенствами с двумя неизвестными называются неравенства вида

где — многочлен двух переменных и . Степенью алгебраического неравенства называется степень многочлена .

4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.

5. Многочлен второй степени

называется также квадратичной функцией двух переменных; многочлен называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.

6. Квадратичную функцию можно записать:

где — матрица квадратичной функции; расширенный (дополненный единицей)
столбец переменных;

б) выделяя квадратичную и линейную части:

7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).

8. Линии, задаваемые системой алгебраических уравнений и неравенств, называются полуалгебраическими. Например, уравнение задает на координатной плоскости полуалгебраическую линию:

9. Теорема 3.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .