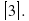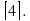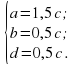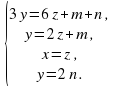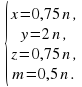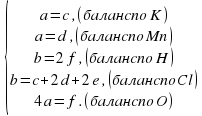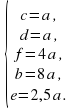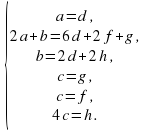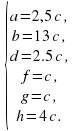Алгебраическое суммирование уравнений химических реакций

Алгебраический метод балансировки (с примерами) — Наука

Видео:Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Содержание:

В балансирующий алгебраический метод Он используется в химии, чтобы уравнять количество атомов по обе стороны химической реакции. Правильно написанная химическая реакция должна иметь формулы всех участвующих реагентов с левой стороны и продуктов с их формулами с правой стороны.

Теперь, когда у вас есть реакция, количество атомов в формулах реагентов не всегда равно количеству соответствующих атомов в формулах продуктов.

Однако масса сохраняется. Например, посмотрим на такую ​​реакцию:

В этом уравнении слева есть соединение, называемое хлоратом калия, которое при нагревании разлагается на хлорид калия и газообразный кислород. Но приглядевшись, мы замечаем, что в молекуле хлората есть 3 атома кислорода, тогда как справа есть только одна молекула газообразного кислорода с 2 атомами.

Затем нужно умножить реагент слева на числовой коэффициент таким образом, чтобы число атомов всех участвующих элементов было одинаковым до и после реакции.

Но… каково значение этого коэффициента?

Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Способы уравновесить уравнения

В приведенном выше уравнении легко определить соответствующие коэффициенты путем осмотра.Если мы умножим на 2 слева, мы получим 2 K атомов, 2 Cl и 6 O атомов.

Поэтому справа мы умножаем хлорид калия на 2 и O₂ по 3:

И теперь мы видим, что учет верен по обе стороны стрелки и реакция была сбалансированной. Обратите внимание, что другие числовые значения также могут привести к сбалансированному уравнению, например:

Однако вы всегда должны искать набор минимальных целых чисел, равных количеству атомов с обеих сторон.

Числа, которые умножают каждую формулу, называются коэффициенты. Очень важно отметить, что коэффициенты можно назначать для баланса, но индексы должны оставаться такими, как они появляются в каждой формуле.

Также нельзя вставлять коэффициенты в середину формулы каждого соединения, так как это изменит ее.

Простые уравнения, подобные приведенному в примере, можно сбалансировать путем проверки или проб и ошибок. Для тех, кто немного сложнее, есть алгебраический метод с серией простых шагов и элементарных арифметических операций, которые подробно описаны ниже.

Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Шаги по алгебраическому уравновешиванию химического уравнения

Видео:Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Шаг 1

-Присвойте каждой молекуле произвольный коэффициент, обозначенный буквой. Обычно буквы a, b, c, d . используются столько, сколько необходимо.

Важный: помни это только коэффициент на молекулу и никогда не зажат посередине, всегда помещается слева.

Видео:Уравнения химический реакций на ОГЭ: как составлять без ошибок?Скачать

Шаг 2

-Составьте список каждого участвующего элемента.

Видео:Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Шаг 3

-Разместите коэффициенты, присвоенные каждому соединению, слева и сопоставьте с коэффициентами справа. Если есть индексы, они умножаются на коэффициент, чтобы найти общее количество атомов.

И если элемент находится более чем в одной молекуле, количество атомов, присутствующих на каждой стороне, добавляется. Таким образом частные уравнения каждого элемента.

Видео:8 класс. Составление уравнений химических реакций.Скачать

Шаг 4

— Числовое значение присваивается только одному из коэффициентов. Обычно это числовое значение равно 1 и присваивается букве, которая встречается чаще всего. Таким образом получается простое уравнение, которое служит отправной точкой для нахождения других коэффициентов.

Видео:Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Шаг 5

-Определите значение следующего коэффициента, используя простую арифметику, и замените его значение другим уравнением, чтобы предложить новое.

Видео:Проклятая химическая реакция 😜 #shortsСкачать

Шаг 6

-Повторите предыдущий шаг замены значений и создания нового уравнения, пока не будут найдены все коэффициенты.

Видео:8 класс.Ч.1.Решение задач по уравнению реакций.Скачать

Шаг 7

-Заменить значения таким образом определенные. Если эти значения являются целыми числами, необходимо убедиться, что уравнение сбалансировано. Если они не были целыми числами, умножьте их на наименьшее общее кратное знаменателей и проверьте баланс.

Далее мы собираемся визуализировать применение этих шагов в разрешении некоторых примеров.

Видео:Типы химических реакций. 1 часть. 8 класс.Скачать

Отработанные примеры балансировки

Видео:Типы Химических Реакций — Химия // Урок Химии 8 КлассСкачать

Пример 1

При необходимости уравновесить следующую реакцию алгебраическим методом:

Видео:Как составлять ХИМИЧЕСКИЕ УРАВНЕНИЯ | 4 лайфхака - 95 ВСЕХ РЕАКЦИЙ в химии!Скачать

Решение

Мы наблюдаем, что реакция не сбалансирована, потому что, хотя есть 2 атома азота с обеих сторон, с кислородом количества слева и справа разные.

Затем мы должны выполнить шаги, описанные в предыдущем разделе:

-Мы снова напишем уравнение и умножим каждую молекулу на другой коэффициент. Строчные буквы выбираются так, чтобы их не перепутать с элементами:

-Теперь мы перечисляем каждый элемент и выравниваем количество указанного элемента слева и справа. Это частные уравнения для каждого элемента:

— Умножая коэффициент и индекс, получаем количество атомов азота. Из уравнения 1 получаем:

-Из уравнения 2 имеем 5-й атомы кислорода слева, а справа 4b Y 2 С:

-Мы присваиваем коэффициенту а значение 1, таким образом:

Этот выбор произвольный, сначала можно выбрать b = 1.

-Эти значения подставляются в уравнение 2 для определения значения c:

-Мы подставляем коэффициенты в исходное уравнение, 1 не нужно писать явно:

-Поскольку предпочтительно, чтобы коэффициенты были целыми числами, все уравнение умножается на наименьшее общее кратное знаменателей, которые равны 2 и 1:

Итак, умножив левый и правый на 2, вы получите:

И подсчитываем количество атомов с обеих сторон, чтобы проверить баланс:

• N налево: 4
• Или осталось: 10
• N правый: 4
• Или вправо: 8 + 2 = 10

Видео:Как решать задачи по химии? Расчет по уравнениям химических реакций | TutorOnlineСкачать

Пример 2

Уравновесить следующую химическую реакцию:

Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Решение

Умножаем каждую молекулу на другой коэффициент:

Далее предлагаем учет каждого элемента справа и слева от стрелки. Всего в реакции 4 элемента: натрий Na; водород H; углерод C и кислород O следует учитывать:

По каждому балансу получаются следующие уравнения:

1) а = 2б
2) а = 2с
3) а = b + d
4) а = 3b + c + 2d

Наиболее распространенный коэффициент к, поэтому присваиваем значение 1:

1) a = 2b ⇒ b = ½
2) a = 2c ⇒ c = ½
3) a = b + d ⇒ d = a — b = 1 — ½ = ½

Подставляем коэффициенты в уравнение:

Мы умножаем обе стороны стрелки на 2, поскольку это единственный имеющийся знаменатель, чтобы исключить дробь:

Мы подсчитываем количество атомов, присутствующих слева: 2 атома Na, H и C и 6 атомов O. Читатель может убедиться, что каждый из них также присутствует справа в равных количествах.

Видео:ЧТО ТАКОЕ уравнение химической реакции? Все намного проще чем ты думал! #shorts #yotubeshortsСкачать

Исследовательский проект «Алгебраический метод расстановки коэффициентов в стехиометрических уравнениях»

Математика – это язык, на котором говорят все точные науки.
Н.И. Лобачевский.
Математика превратила химию из описательной науки в экспериментальную, и именно математика сделала химию наукой. С помощью математики мы производим расчёты по химическим формулам и решаем уравнения химических реакций, моделируем химические процессы как в живой, так и неживой природе. Без математики невозможно ни одно химическое производство. Если на мгновение представить, что было бы, если из химии исчезли числа и математические расчёты… Мир бы лишился пищи, лекарств, красок, фотоплёнок, минеральных удобрений, пластмасс, металлических сплавов и многих других полезных веществ и вещей.
Математика для химиков – это, в первую очередь, полезный инструмент решения многих химических задач. В школьном курсе химии при решении сложных уравнений окислительно-восстановительных реакций возникают большие трудностив расстановке коэффициентов.Так как очень трудно найти какой-либо раздел математики, который совсем не используется в химии, возникла мысль применить математические знания к разрешению химических проблем. Можно ли сопоставить уравнения в химии и математике? Существует ли иной, математический метод расстановки коэффициентов в химических уравнениях?Вот вопросы, которые побудили нас заняться исследованием данной проблемы. Изучить новый подход к решению химических задач, заинтересовать старшеклассников — веское доказательство актуальности данной работы.

2. Цель исследования:
изучить алгебраический метод расстановки коэффициентов в химических уравнениях и обосновать его применение к решению задач.

Задачи:
Изучить источники информации по данной теме.
Выявить приемы решения химических задач алгебраическим методом.
Показать использование алгебраического метода при решении химических уравненийокислительно-восстановительных реакций.
Составить алгоритм нахождения коэффициентов в химических уравнениях.
Объект исследования: окислительно-восстановительные уравнения химических реакций.
Методы исследования:теоретический анализ литературы по данной проблеме, сравнительный анализ, синтез, моделирование и обобщение.
Гипотеза: алгебраический метод решения уравнений химических реакций позволяет упростить процесс нахождения коэффициентов в уравнениях.
Теоретическая значимость исследования заключается в изучении алгебраического метода и его применении для решения задач, а практическая — состоит в возможности использования данного материала на уроках химии и при подготовке к ОГЭ и ЕГЭ.

Просмотр содержимого документа
«проект на НПК»

ОКРУЖНАЯ НАУЧНО – ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ

Алгебраический метод расстановки коэффициентов

в стехиометрических уравнениях

Автор: Богданова Светлана, ученица 9 класса

ГБОУ СОШ с. Бобровка.

ОУ: государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Бобровка

муниципального района Кинельский Самарской области

Научный руководитель: Саликова Людмила Александровна, учитель математики.

Обоснование и актуальность проблемы……………………………….. 2

Цель и задачи исследовательского проекта…………………………. 2-3

Анализ источников информации по данной проблеме…………………. 4

2.2. Правила составления уравнений…………………………………….4 — 5

Расстановка коэффициентов в уравнения……………………………5-7

1.Обоснование гипотезы и выводы……………………………………. 7-11

Обоснование и актуальность проблемы.

Математика – это язык, на котором говорят все точные науки.

Н.И. Лобачевский

Математика превратила химию из описательной науки в экспериментальную, и именно математика сделала химию наукой. С помощью математики мы производим расчёты по химическим формулам и решаем уравнения химических реакций, моделируем химические процессы как в живой, так и неживой природе. Без математики невозможно ни одно химическое производство. Если на мгновение представить, что было бы, если из химии исчезли числа и математические расчёты… Мир бы лишился пищи, лекарств, красок, фотоплёнок, минеральных удобрений, пластмасс, металлических сплавов и многих других полезных веществ и вещей.

Математика для химиков – это, в первую очередь, полезный инструмент решения многих химических задач. В школьном курсе химии при решении сложных уравнений окислительно-восстановительных реакций возникают большие трудностив расстановке коэффициентов.Так как очень трудно найти какой-либо раздел математики, который совсем не используется в химии, возникла мысль применить математические знания к разрешению химических проблем. Можно ли сопоставить уравнения в химии и математике? Существует ли иной, математический метод расстановки коэффициентов в химических уравнениях?Вот вопросы, которые побудили нас заняться исследованием данной проблемы. Изучить новый подход к решению химических задач, заинтересовать старшеклассников — веское доказательство актуальности данной работы.

2. Цель исследования:

изучить алгебраический метод расстановки коэффициентов в химических уравнениях и обосновать его применение к решению задач.

Изучить источники информации по данной теме.

Выявить приемы решения химических задач алгебраическим методом.

Показать использование алгебраического метода при решении химических уравненийокислительно-восстановительных реакций.

Составить алгоритм нахождения коэффициентов в химических уравнениях.

Объект исследования: окислительно-восстановительные уравнения химических реакций.

Методы исследования:теоретический анализ литературы по данной проблеме, сравнительный анализ, синтез, моделирование и обобщение.

Гипотеза: алгебраический метод решения уравнений химических реакций позволяет упростить процесс нахождения коэффициентов в уравнениях.

Теоретическая значимость исследования заключается в изучении алгебраического метода и его применении для решения задач, а практическая — состоит в возможности использования данного материала на уроках химии и при подготовке к ОГЭ и ЕГЭ.

Понятийный аппарат

Химическим уравнением (уравнением химической реакции) 1 — называют условную запись химической реакции с помощью химических формул, числовых коэффициентов и математических символов.

Стехиометрия 2 (от др.-греч. στοιχεῖον «элемент» + μετρέω «измерять») — раздел химии о соотношениях реагентов в химических реакциях.

Реагенты 3 – химические препараты, предназначенные для химического анализа научно-исследовательских, различных лабораторных работ.

Закон сохранения массы 4 гласит, что количество вещества каждого элемента до реакции равняется количеству вещества каждого элемента после реакции.

стехиометрическое уравнение 5 — уравнение, показывающее количественные соотношения реагентов и продуктов химической реакции.

коэффициенты 6 –натуральные числа, стоящие перед формулами веществ.

Анализ источников информации по данной проблеме.

История науки говорит о том, что на границах различных областей знания могут происходить очень интересные события. И хотя химики и математики мыслят совсем по-разному, те случаи, когда им удается взаимодействовать, приводят к появлению красивых и нетривиальных результатов и способствуют обогащению обеих наук.

В Конце XVIII — начале XIX вв.началось становлениезаконов стехиометрии.У истоков этих исследований стоял немецкий ученый И. В. Рихтер. В студенческие годы на него большое впечатление произвели слова его учителя — философа И. Канта о том, что в отдельных направлениях естественных наук истинной науки столько, сколько в ней математикиРихтер посвятил свою диссертацию использованию математики в химии. В своих научных работах Рихтер стремился отыскать математические зависимости в химических реакциях.Не будучи, в сущности, химиком, Рихтер ввел первые количественные уравнения химических реакций 1 ,стал использовать термин стехиометрия 2 .

Видео:Балансирование химических уравненийСкачать

Правила составления уравнений.

Уравнение химической реакции даёт качественную и количественную информацию о химической реакции, реагентах 3 и продуктах реакции; его составление основывается на законе сохранения массы 4 веществ в химических реакциях

Составляя стехиометрическое уравнение 5 , вего левой части записывают формулывеществ, вступивших в реакцию, соединяя их знаком «плюс», а в правой части записывают формулыобразовавшихся веществ, также соединенных знаком «плюс». Между частями уравнения ставят стрелку. Получают схему реакции. Затем, используя закон сохранения массы веществ, находят коэффициенты 6 так, чтобы число атомов одинаковых элементов в левой и правой частях уравнения было равным

Чтобы превратитьсхему реакции в химическое уравнение, нужно подобрать коэффициенты для каждого вещества (в случаенеобходимости), записать их перед химическими формулами и заменить стрелку на знак равенства. Мы не ставим перед собой задачу научить составлять химические уравнения.Для того чтобы это сделать, нужно «совсем чуть-чуть» – знать свойства элементов.Практически же, даже высококвалифицированный химик не всегда «с ходу» может написать продукты реакции для данных исходныхвеществ.

Дальнейшее изложение относится только к ситуации, когда составленасхема реакции, т.е. известны формулы исходных веществ и продуктов, ноне известны стехиометрические коэффициенты в уравнении.

Видео:Составление уравнений химических реакций. 2 часть. 8 класс.Скачать

Расстановка коэффициентов в уравнениях.

Одним из способов уравнивания количества атомов в химическом уравнении является подбор коэффициентов методом проб и ошибок. В простых уравнениях реакций расстановка коэффициентов не вызывает большого затруднения: находится наименьшее общее кратное количества атомов и уравниваются правая и левая части. Сложно расставлять коэффициенты в уравнениях реакций, где число веществ, вступающих и образующихся в результате реакции более двух. В таких уравнениях подбор коэффициентов проводят методом электронного баланса, который носит не строго формализованный характер и имеет свои тонкости.

В ходе анализа источников информации по теме мы убедились, что существуети формально математический метод нахождениякоэффициентов, пригодный для разных химических реакций, которыйоснован на законе сохранения массы. Он называется алгебраическим. Наиболее подробно этот метод был изложен в записках профессора С. Г. Крапивина.

Оценивания алгебраический метод, профессор С.Г. Крапивин отмечает, что «все дело сводится к подсчету и комбинированию количеств атомов различных элементов для составления системы уравнений. Химическая сторона вопроса здесь не затрагивается».

Для нахождения коэффициентов необходимо ввести неизвестные, при этом общее количество неизвестных должно равняться количеству реагирующих веществ. Затем, опираясь на число атомов каждого элемента, составляется система уравнений. Число уравнений в системе должно равняться числу химических элементов, участвующих в реакции.

Математические уравнения и методы, используемые в химии, имеют дело с конкретными свойствами атомов и молекул, которые подчиняются естественным природным ограничениям. Иногда эти ограничения бывают довольно жесткими и приводят к резкому сужению числа возможных решений математических уравнений. Математические уравнения, применяемые в химии, а также их решения должны иметь химический смысл. Поэтому на решения системы накладываются ограничения: решения системы должны быть натуральными и взаимно простыми.

Рассмотрим применение алгебраического метода на примере конкретной окислительно-восстановительной реакции, схема которой

HNO ₂ → HNO ₃ + NO + Н₂О

Поставим в уравнение реакции коэффициенты в алгебраической форме,т.е. буквенные

Опираясь на число атомов в каждом из соединений, составим систему уравнений материального баланса по каждому элементу (число атомов каждого элемента слева и справа от знака равенствадолжно быть одинаково):

a = b + 2d (баланс по водороду);

a = b + c (баланс по азоту);

2a = 3b + c + d (баланс по кислороду).

Таким образом, мы получили систему из 3 линейных уравнений с 4 неизвестными.

Решим систему линейных уравнений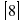. Преобразуем уравнения таким образом, чтобы все коэффициенты были выражены через какой-либо один, например, c:

Используя требования натуральности коэффициентов и условие, что они должны быть взаимно простыми, нетрудно увидеть, что c=2, a = 3, b=1 и d=1. Итак, уравнение имеет вид:

Проверка правильности расстановки коэффициентов в любом химическом уравнении производится подсчетом количества атомов кислорода, если в левой и правой части количество атомов кислорода одинаково, значит, коэффициенты расставлены правильно.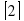

Рассмотрим применение алгебраического метода для более сложных стехиометрических уравнений.

Составить уравнение реакции: Cu + HNO ₃ → Cu ( NO ₃)₂ + NO + H ₂ O

Расставляем алгебраические коэффициенты.

2.Опираясь на число атомов в каждом из этих соединений, составляем уравнения материального баланса.

3 y = 6 z + m + n (по кислороду)

y = 2 z + m (по азоту)

y = 2 n ( по водороду)

3.Составляем систему уравнений.

Заметим, что в полученной системе 4 уравнения и 5 неизвестных.

4.Выражаем все коэффициентычерез n .

Умножим второе уравнение на 3 и вычтем из первого, получим m = 0,5 n .

Выразим из второго уравнения z , получим: z = = 0,75 n .

Итак,

Очевидно, что для натуральных и «несокращаемых» коэффициентов n = 4, значит

x = 3, y = 8, z = 3, m = 2.

Окончательный вид уравнения:

Составить уравнение реакции:

Расставляем алгебраические коэффициенты.
aKMnO ₄ + bHCl = cKCl + dMnCl ₂ + eCl ₂ + fH ₂ O

Составляем систему уравнений материального баланса по каждому элементу.

Заметим, что в полученной системе 5 уравнений и 6 неизвестных.

Выражаем все коэффициенты через а:

Получаем:
a=c=d=2; e=5; b=16; f=8.
Уравнение принимает вид:

2 KMnO ₄ +16 HCl =2 KCl +2 MnCl ₂ +5 Cl ₂ +8 H ₂ O .
Пример 3.

Составить уравнение реакции:

Коэффициенты этого уравнения вряд ли можно легко подобрать, а вот

алгебраический метод нас не подведет.

1. Расставляем алгебраические коэффициенты

2.Составляем систему уравнений материального баланса по каждому элементу.

Заметим, что в полученной системе 6 уравнений и 7 неизвестных.

3.Теперь выражаем все коэффициенты через c:

Очевидно, что для натуральных и «несокращаемых» коэффициентов

c=2, а=5, b =26, d =5, f = g =2, h =8.

Окончательный вид уравненияокислительно – восстановительной реакции:

Рассматривая примеры, можно сделать вывод:если число уравнений материальногобаланса на единицу меньше числа коэффициентов, т.е. числа веществ, тоалгебраический метод позволяет однозначно находить коэффициенты, неприбегая ни к каким дополнительным соображениям.

Известны такие реакции, где число веществ меньше чем число входящих в них элементов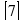. Рассмотрим такую реакцию.
Пример 4.
FeCl ₃ + KCNS → KCl+ Fe(CNS) ₃

Заметим, что группа атомов(CNS) переходит из одних веществ в другие, не изменяясь.
1.Расставляем алгебраические коэффициенты и составляем систему уравненийматериального баланса.
aFeCl ₃ + bKCNS = cKCl+ dFe(CNS) ₃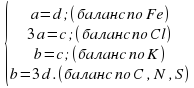
Мы видим, что уравнения по С, N , S повторяются.

Отсюда 3a=b=c=3d, в простом случае a=d=1; b=c=3.
Получаем уравнение.
FeCl ₃ + 3KCNS = 3KCl+ Fe(CNS) ₃

Значит, алгебраический метод можно применять и к реакциям, где число веществ меньше чем число входящих в них элементов.

На основе проделанной работыможно составить алгоритм нахождения коэффициентов в стехиометрических уравнениях алгебраическим способом.

Для нахождения коэффициентов в стехиометрических уравнениях алгебраическим способом поступают следующим образом:

Обозначают все неизвестные коэффициенты переменными.

Составляют уравнения материального баланса, опираясь на число атомов в каждом из этих соединений.

Составляют систему линейных уравнений.

Решают полученную систему уравнений, выражая все коэффициенты через один из них.

Истолковывают результат, учитывая ограничения, применяемые в химии (решения системы должны быть натуральными и взаимно простыми).

Записывают получившееся уравнение.

Данная работа предназначена для наиболее любознательного читателя. Проведенные исследования оказались важными и значимыми, так как с их помощью был найден новый прием решения стехиометрических уравнений.

В ходе исследований подтверждена истинность выдвинутой гипотезы: представленный алгебраический метод позволяет существенно упростить процесс нахождения коэффициентов в уравнениях химических реакций.Но этим методом может пользоваться лишь тот, кто владеет техникой решения систем линейных уравнений. Хочется надеяться, что данная работа окажет помощь учащимся 9,11 классов при подготовке к экзаменам, а также будет интересна всем тем, кто увлекается математикой.

АбкинГ.Л., Методикарешениязадачпохимии.Пособиедляучителей. М., «Просвещение», 1971.

Берг Л.Г., Громаков С.Д.,Зороацкая И.В.,Аверко-Антонович И.Н. Способы подбора коэффициентов в химических уравнениях — Казань: изд-во Казанского ун-та, 1959.

Википедия — свободная энциклопедия. http://ru.wikipedia.org/

Габриелян О. С., Химия. 9 класс- М.: Дрофа, 2010.

Лиман М.М., Школьникам о математике и математиках: пособие для учащихся сред.школы.М.: Просвещение,1981.

Левицкий М. Язык химиков // Химия и жизнь. – 2000. –№1.

СрагоИ.А.,Окислительно-восстановительные реакции. Конспект лекций.http://window.edu.ru/library/

Цыпкин А.Г.,Пинский А.И., Справочное пособие по методам решения задач по математике. М.: «Наука»,1983

Просмотр содержимого презентации
«презентация к проекту»

Математика –это язык,

на котором говорят все точные науки Н. И. Лобачевский

Алгебраический метод расстановки коэффициентов

в стехиометрических уравнениях

Автор: Богданова Светлана, ученица 9 класса ГБОУ СОШ с. Бобровка Руководитель: Саликова Людмила Александровна, учитель математики

Алгебраический метод расстановки коэффициентов

в стехиометрических уравнениях

Цель работы : изучить алгебраический метод расстановки коэффициентов в химических уравнениях и обосновать его применение к решению задач.

• Изучить источники информации по данной теме.
• Выявить приемы решения химических задач алгебраическим методом.
• Показать использование алгебраического метода при решении химических уравнений окислительно-восстановительных реакций.
• Составить алгоритм нахождения коэффициентов в химических уравнениях алгебраическим методом.

алгебраический метод решения уравнений позволяет упростить процесс нахождения коэффициентов в стехиометрических уравнениях.

Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. Д. Сантаяна

Способы расстановки коэффициентов

в химических уравнениях

• подбор коэффициентов методом проб и ошибок;

• метод электронного баланса;

• математический метод (алгебраический).

«…все дело сводится к подсчету и комбинированию количеств атомов различных элементов для составления системы уравнений. Химическая сторона вопроса здесь не затрагивается»

Профессор С.Г. Крапивин

Схема химической реакции:

HNO 2 → HNO 3 + NO + Н 2 О

Химическое уравнение: a HNO 2 = b HNO 3 + c NO + d Н 2 О

Уравнения материального баланса:

a = b + 2d (баланс по водороду);

a = b + c (баланс по азоту);

2a = 3b + c + d (баланс по кислороду).

d=0,5c; b+c-3d=0 отсюда b=0,5c;

Человек, не знающий математики, не способен ни к каким другим наукам. Роджер Бэкон

Таким образом, все коэффициенты выражены через с

Используя требования натуральности коэффициентов и

условие, что они должны быть взаимно простыми, нетрудно

увидеть, что c=2, тогда a = 3, b=1 и d=1.

Итак, уравнение имеет вид:

составить уравнение реакции:

1. Расставляем алгебраические коэффициенты.

х Cu + y HNO 3 = z Cu (NO 3 ) 2 + m NO + n H 2 O

2. Составляем уравнения материального баланса и получаем систему из четырех уравнений с пятью неизвестными:

3. Выражаем все коэффициенты через n.

Умножим второе уравнение на 3 и вычтем из первого, получим m = 0,5n.

Выразим из второго уравнения z, получим: z= = 0,75n.

4. Для натуральных и «несокращаемых» коэффициентов n = 4 , значит

x = 3, y = 8, z = 3, m = 2.

Окончательный вид уравнения:

Математика –это язык,

на котором говорят все точные науки. Н. И. Лобачевский

Вывод: если число уравнений материального баланса на единицу меньше числа коэффициентов, т.е. числа веществ, то алгебраический метод позволяет однозначно находить коэффициенты, не прибегая ни к каким дополнительным соображениям .

В каждой естественной науке заключено столько истины, сколько в ней есть математики. И. Кант

Заметим, что группа атомов(CNS) переходит из одних веществ в другие,

1.Расставляем алгебраические коэффициенты

а FeCl 3 + b KCNS= c KCl+ d Fe(CNS) 3 и составляем систему

уравнений материального баланса.

Мы видим, что уравнения по С,N,S повторяются .

Отсюда 3a=b=c=3d , в простом случае a=d=1; b=c=3 .

Получаем уравнение. FeCl 3 + 3KCNS = 3KCl+ Fe(CNS) 3

алгебраический метод можно применять и к реакциям, где число веществ меньше чем число входящих в них элементов.

Математика –это язык,

на котором говорят все точные науки Н. И. Лобачевский

Для нахождения коэффициентов в стехиометрических уравнениях поступают следующим образом: 1 .Обозначают все неизвестные коэффициенты переменными. 2 .Составляют уравнения материального баланса, опираясь на закон сохранения массы. 3 .Составляют систему линейных уравнений. 4 .Решают полученную систему уравнений, выражая все коэффициенты через один из них. 5 .Истолковывают результат, учитывая ограничения, применяемые в химии (решения системы должны быть натуральными и взаимно простыми). 6 .Записывают получившееся уравнение.

Математика –это язык,

на котором говорят все точные науки Н. И. Лобачевский

Представленный алгебраический метод позволяет существенно упростить процесс нахождения коэффициентов в уравнениях химических реакций для тех, кто владеет техникой решения систем линейных уравнений .

Математика –это язык,

на котором говорят все точные науки Н. И. Лобачевский

Библиография 1.АбкинГ.Л., Методика решения задач похимии.Пособиедляучителей. М., «Просвещение», 1971. 2.Берг Л.Г., Громаков С.Д.,Зороацкая И.В.,Аверко-Антонович И.Н. Способы подбора коэффициентов в химических уравнениях — Казань: изд-во Казанского ун-та, 1959. 3.Википедия — свободная энциклопедия. http://ru.wikipedia.org/ 4.Габриелян О. С., Химия. 9 класс- М.: Дрофа, 2010. 5.Лиман М.М., Школьникам о математике и математиках: пособие для учащихся сред.школы.М.: Просвещение,1981. 6.Левицкий М. Язык химиков // Химия и жизнь. – 2000. –№1. 7.СрагоИ.А.,Окислительно-восстановительные реакции. Конспект лекций.http://window.edu.ru/library/ 8.Цыпкин А.Г.,Пинский А.И., Справочное пособие по методам решения задач по математике. М.: «Наука»,1983

Математика –это язык,

на котором говорят все точные науки Н. И. Лобачевский

Видео:Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать

Как решать задачи по химии. Расчет по уравнениям химических реакций.

Как решать задачи по химии? Как проводить простейшие расчеты по уравнениям химических реакций? Сколько выделяется газа, образуется воды, выпадает осадка или сколько получается конечного продукта реакций? Сейчас мы постараемся разобрать все нюансы и ответить на эти вопросы, которые очень часто возникают при изучении химии.

Решение задач в химии является неотъемлемой частью в изучении этой сложной, но очень интересной науки.

Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Алгоритм решения задач по химии

1. Прочитать условия задачи (если они есть). Да, об этом все знают — как же решить задачу без условий — но все же, для полноты инструкции, мы не могли не указать этот пункт.
2. Записать данные задачи. На этом пункте мы не будем заострять внимание, так как требования различных учебных заведений, учителей и преподавателей могут значительно отличаться.
3. Записать уравнение реакции. Теперь начинается самое интересное! Здесь нужно быть внимательным! Обязательно необходимо верно расставить коэффициенты перед формулами веществ. Если вы забудете это сделать, то все наши усилия буду напрасны.
4. Провести соответствующие расчеты по химическому уравнению. Далее рассмотрим, как же сделать эти самые расчеты.

Для этого у нас есть два пути, как решить задачу по химии. Условно, назовем их правильным (используя понятия количества вещества) и неправильным (используя пропорции). Конечно же, мы бы рекомендовали решать задачи правильным путем. Так как у неправильного пути имеется очень много противников. Как правило, учителя считают, что ученики, решающие задачи через пропорции, не понимают самой сути протекания процессов химических реакций и решают задачи просто математически.

Расчет по уравнениям химических реакций с использованием понятия количества вещества

Суть данного метода, состоит в том, что вещества реагируют друг с другом в строгом соотношении. И уравнение реакции, которое мы записали ранее, дает нам это соотношение. Коэффициенты перед формулами веществ дают нам нужные данные для расчетов.

Для примера, запишем простую реакцию нейтрализации серной кислоты и гидроксида натрия.

H_SO_ + NaOH → Na_SO_ + H_O

H_SO_ + 2NaOH → Na_SO_ + 2H_O

Исходя из этого уравнения, мы видим, что одна молекула серной кислоты взаимодействует с двумя молекулами гидроксида натрия. И в результате этой реакции получается одна молекула сульфата натрия и две молекулы воды.

Сейчас мы немного отступим от разбора задач, чтобы познакомиться с основными понятиями, которые пригодятся нам в решении задач по химии.

Рассчитывать количество молекул, например в 98 граммах серной кислоты — это не самое удобное занятие. Числа будут получаться огромными ( ≈ 6,022140857⋅10 23 молекул в 98 граммах серной кислоты) . Для этого в химии ввели понятие количества вещества (моль) и молярная масса.

1 Моль (единица измерения количества вещества) — это такое количество атомов, молекул или каких либо еще структурных единиц, которое содержится в 12 граммах изотопа углерода-12. Позднее выяснилось, что в 12 граммах вещества углерод-12 содержится 6,022140857⋅10 23 атомов. Соответственно, можно сказать, что 1 моль, это такая масса вещества, в которой содержится 6,022140857⋅10 23 атомов (или молекул) этого вещества.

Но ведь молекулы и атомы имеют различный состав и различное строение. Разные атомы содержат разное количество протонов и нейтронов. Соответственно 1 моль для разных веществ будет иметь разную массу, имея при это одинаковое количество молекул ( атомов). Эта масса называется молярной.

Молярная масса — это масса 1 моля вещества.

Используя данные понятия, можно сказать, что 1 моль серной кислоты реагирует с 2 молями гидроксида натрия, и в результате получается 1 моль сульфата натрия и 2 моль воды. Давайте запишем эти данные под уравнением реакции для наглядности.

beginH_SO_ & + & 2NaOH & → & Na_SO_ & + & 2H_O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль end

Следом запишем молярные массы для этих веществ

begin H_SO_ & + & 2NaOH & → & Na_SO_ & + & 2H_O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г end

Теперь, зная массу одного из веществ, мы можем рассчитать, сколько нам необходимо второго вещества для полного протекания реакции, и сколько образуется конечных продуктов.

Для примера, решим по этому же уравнению несколько задач.

Задача. Сколько грамм гидроксида натрия (NaOH) необходимо для того, чтобы 49 грамм серной кислоты (H₂SO₄) прореагировало полностью?

Итак, наши действия: записываем уравнение химической реакции, расставляем коэффициенты. Для наглядности, запишем данные задачи над уравнением реакции. Неизвестную величину примем за Х. Под уравнением записываем молярные массы, и количество молей веществ, согласно уравнению реакции:

begin49 : г & & X : г & & & & \ H_SO_ & + & 2NaOH & → & Na_SO_ & + & 2H_O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г end

Записывать данные под каждым веществом — не обязательно. Достаточно это будет сделать для интересующих нас веществ, из условия задачи. Запись выше дана для примера.

Примерно так должны выглядеть данные, записанные по условиям задачи. Не претендуем на единственно правильное оформление, требования у всех разные. Но так, как нам кажется, смотрится все довольно наглядно и информативно.

Первое наше действие — пересчитываем массу известного вещества в моли. Для этого разделим известную массу вещества (49 грамм) на молярную массу:

4998=0,5 моль серной кислоты

Как уже упоминалось ранее, по уравнению реакции 1 моль серной кислоты реагирует с 2 моль гидроксида натрия. Соответственно с 0,5 моль серной кислоты прореагирует 1 моль гидроксида натрия.

n(NaOH)=0.5*2=1 моль гидроксида натрия

Найдем массу гидроксида натрия, умножив количество вещества на молярную массу:

1 моль * 40 г/моль = 40 грамм гидроксида натрия.

Ответ: 40 грамм NaOH

Как видите, в решении задачи по уравнению реакции нет ничего сложного. Задача решается в 2-3 действия, с которыми справятся ученики начальных классов. Вам необходимо всего лишь запомнить несколько понятий.

Решение задач по химии через пропорцию

Ну и расскажем про второй способ вычислений по уравнениям химических реакций — вычисления через пропорцию. Этот способ может показаться немного легче, так как в некоторых случаях можно пропустить стадию перевода массы вещества в его количество. Чтобы было более понятно, объясню на том же примере.

Так же, как и в прошлом примере, запишем уравнение реакции, расставим коэффициенты и запишем над уравнением и под уравнением известные данные.

Для этого способа, нам так же понадобится записать под уравнением реакции, следом за молярной массой, массу вещества, соответствующую его количеству по уравнению. Если проще, то просто перемножить две строки под уравнением реакции, количество моль и молярную массу. Должно получиться так:

begin49 : г & & X : г & & & & \ H_SO_ & + & 2NaOH & → & Na_SO_ & + & 2H_O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г \ 98 : г & & 80 : г & & 142 : г & & 36 : г end

А теперь внимание, начинается магия! Нас интересует строка данных над уравнением, и самая нижняя строка под уравнением. Составим из этих данных пропорцию.

Далее находим неизвестное значение Х из пропорции и радуемся полученному значению:

Х=49*80/98=40 грамм

Как видим, получается тот же результат. Прежде всего, при решении задач в химии, главное все же — понимание химических процессов. Тогда решение задачи не станет для вас проблемой!