Алгебраический метод решения уравнений с параметрами

Видео:Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Аналитический методСкачать

Алгебраические уравнения высших степеней с параметрами

Разделы: Математика

1.1. Общая методическая концепция решения уравнений с параметрами

Пусть дано уравнение F(x, a) = 0, (1)

если ставится задача для каждого значения а А решить уравнение (1) относительно х, т.е. получить уравнение

то уравнение (1) называется уравнением с неизвестным х и параметром а. А – область изменения параметра. Принято считать, что А – множество действительных чисел. Решить уравнение (1) – значит решить множество уравнений, которые получаются из уравнения (1) при а R. Сделать это можно, если по некоторому признаку разбить множество А на подмножества и решить заданное уравнение на каждом из них. Значения а называются контрольными.

1.2. Использование параметра как равноправной переменной

Некоторые уравнения бывает целесообразно решать, рассматривая их как уравнение именно относительно параметра, который фигурирует в условии, а не относительно искомой переменной. Этот путь эффективен, в частности, в тех случаях, когда степень переменной относительно высока, а степень параметра равна двум.

Пример 1. Решить уравнение с параметром.

2x 3 – (а+2)х 2 – ах + а 2 = 0 (1)

Решение: Данное уравнение можно рассматривать как квадратное относительно параметра а, переписав его в виде:

а 2 – х(х+1)а – 2х 2 + 2х 3 = 0 (2)

Найдем дискриминант D.

D = х 2 (х+1) 2 – 8(х 3 – х 2 ) = х 4 — 6х 3 + 9х 2 = х 2 (х 2 — 6х + 9) = х 2 (х — 3) 2 .

Найдем корни уравнения (2).

; а₂ = 2х.

Получим уравнение (а – х 2 + х)(а – 2х) = 0 равносильное исходному уравнению, которое ещё в свою очередь равносильно совокупности

Рассмотрим уравнение х 2 – х – а = 0, D = 1 – 4а.

D = 0 при а = -1/4 один корень х = 1/2

D 0 при а > -1/4 два корня

Рассмотрим уравнение х = а/2, при а = -1/4, х = -1/8.

Ответ: при а > -1/4 три корня: х1 = а/2,

при а = -1/4 два корня: х1 = -1/8; х 2 = ½

при а 4 – (а+2)х 3 – (а – 1)х 2 + (а 2 – 1) = 0;

1.3. Графический способ решения уравнений с параметрами

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. В самом деле, поскольку параметр «равен в правах» с переменной, то ему, естественно можно выделить и свою координатную ось. Таким образом, возникает координатная плоскость (х; а). Рассмотрим примеры.

Пример 1. В зависимости от параметра а определить число корней уравнения.

x 4 – 10х 3 – 2(а — 11)х 2 + 2(5а + 6)х + 2а + а 2 = 0;

Решение. Рассмотрим это уравнение как квадратное относительно а.

а 2 + 2а(1 + 5х – х 2 ) + (х 4 – 10х 3 + 22х 2 + 12х) = 0;

D/4 = 1 + 25х 2 + х 4 + 10х – 10х 3 – 2х 2 – х 4 + 10х 3 – 22х 2 – 12х = х 2 – 2х +1 = = (х – 1) 2

Найдем а₁ и а₂ ; а₁ = х 2 -5х – 1 + х – 1 = х 2 — 4х – 2;

а₂ = х 2 -5х – 1 — х + 1 = = х 2 – 6х.

Теперь обращаемся к координатной плоскости (х; а).

х 2 — 4х – 2 = х 2 – 6х, 2х = 2, х = 1, а(1) = -5.

Ответ: если а -5, то четыре решения.

Упражнения

Найти все значения параметра а, при каждом из которых уравнение имеет три решения.

1. (х 2 – 12а) 2 – 24х 2 + 32х + 96а = 0;
2. (2х 2 – а) 2 – 24х 2 + 16х + 4а = 0;
3. (2х 2 – а) 2 = 13х 2 + 6х – 2а = 0.

1.4. Использование свойств функций для решения алгебраических уравнений

На выпускных экзаменах за курс средней школы встречаются уравнения с параметром, решение которых связано с использованием четности функций. Напомним определение четности функции.

Определение. Функция f(x) называется четной, если f(-x) = f(x) для любого х из области определения этой функции. График четной функции симметричен относительно оси ординат. У четной функции область определения симметрична относительно начала координат.

Пример 1. Может ли при каком-нибудь значении а уравнение

2х 8 – 3ах 6 + 4х 4 – ах 2 = 5 иметь 5 корней?

Решение. Обозначим f(x) = 2х 8 – 3ах 6 + 4х 4 – ах 2 . f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х₀ – тоже, х = 0 не является корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого уравнения при любом действительном а четно, поэтому 5 корней оно иметь не может.

Пример 2. При каком значении а уравнение х 10 – а|х| + a 2 – а = 0 имеет единственное решение?

Решение. Обозначим f(x) = х 10 – а|х| + a 2 – а, f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х₀ – тоже. Значит для единственности решения необходимо, чтобы х₀ = 0. В этом случае из уравнения получим: a 2 – а = 0, а = 0 или а = 1. Проверим достаточность каждого из полученных значений параметра а,

при а = 0, х 10 = 0, т.е. х = 0 единственное решение.

при а = 1, х 10 — |x| = 0. Корнями являются числа ± 1, 0.

Ответ: при а = 0 уравнение имеет единственное решение.

Упражнения

1. Может ли при каком-нибудь а уравнение 2х 6 – х 4 – ах 2 = 1 иметь три корня?
2. Может ли при каком-нибудь а уравнение 2х 6 – 2ах 4 + 3х 2 = 4 иметь пять корней?
3. При каком значении а уравнение имеет единственное решение?

1.5. Метод замены

Как мы уже знаем, что рациональное и быстрое решение уравнения зависит от замены переменной. Рассмотрим примеры, для решения которых нужны специальные замены, которые приводят как раз к быстрому решению уравнений.

Пример 1. Решить уравнение (х + 2а)(х +3а)(х + 8а)(х + 12а) = 4а 2 х 2 ,

где а – параметр.

Решение. Данное уравнение относится к уравнению вида

(х + а)(х +b)(х + c)(х + d) = Eх 2 (см. п. 2.5 (3))

Используя специфику решения такого уравнения, будем иметь:

(х 2 + 14ах +24а 2 )( х 2 + 11ах +24а 2 ) = 4а 2 х 2

Если а = 0, то х = 0.

Обратно, если а ≠ 0, то х ≠ 0.

Разделим обе части этого уравнения на а 2 х 2 , будем иметь

В полученном уравнении сделаем подстановку и получим уравнение (у + 14)(у + 11) = 4, у 2 + 25у + 150 = 0, у₁ = — 15, у₂ = — 10.

Таким образом, получим два уравнения

и

Решим первое уравнение х 2 + 15ах + 24а 2 = 0, D = 129a 2 , х_1,2

Решим второе уравнение х 2 + 10ах + 24а 2 = 0, D = 4a 2

х 3 = -6а, х 4 = -4а

Ответ: если а = 0, то х = 0
если а ≠ 0, то х_1,2, х 3 = -6а, х 4 = -4а

Упражнения

1. Найдите все действительные значения величины а, при которых уравнение х(х +1)(х + а)(х + 1 + а) = а 2 имеет четыре действительных корня.
2. Решить уравнение х 4 + а 4 – 3ах 3 + 3а 2 х = 0.
3. При каких значениях а уравнение (х 2 – 2х) 2 — (а + 2)(х 2 – 2х) + 3а – 3 = 0 имеет четыре корня?
4. Решить уравнение (х + а)(х + 2а)(х + 3а)(х + 4а) = 3а 4

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Уравнения с параметром — алгоритмы и примеры решения

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

Видео:9 класс, 7 урок, Задачи с параметрамиСкачать

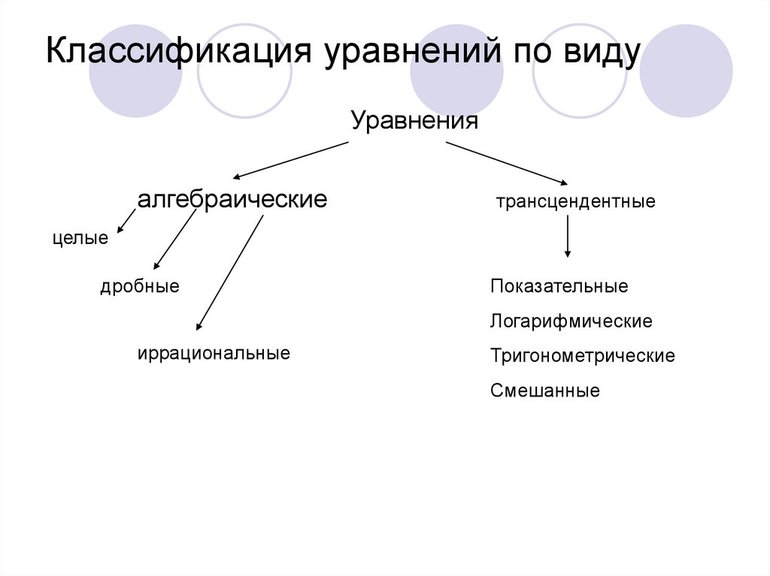
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Видео:8 класс, 39 урок, Задачи с параметрамиСкачать

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

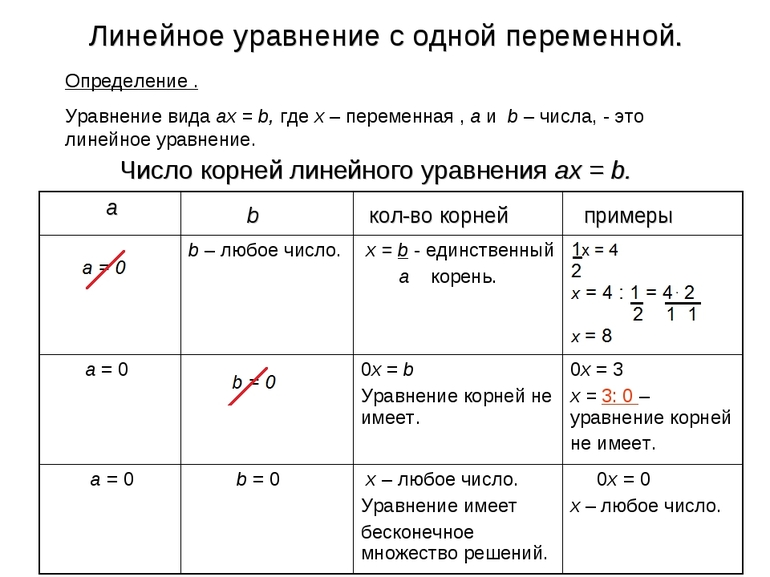
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: ^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Уравнения с параметром

Что нужно знать

• Способы решения алгебраических уравнений. Особое внимание следует уделить исследованию квадратных уравнений ;
• Способы построения и преобразования графиков элементарных функций.

Видео:Уравнения с параметрами | Алгебра 11 класс #32 | ИнфоурокСкачать

Параметр

Параметр – фиксированное, но неизвестное число, обозначенное буквой.

Чему равно решение уравнения 3 x + a = 0 3x+a=0 3 x + a = 0 при a = 3 a=3 a = 3 ?

Простейшие примеры

В некоторых задачах требуется найти значение параметра, при котором известное число является решением уравнения. Проще всего подставить это число в уравнение и найти значение параметра, при котором равенство является верным.

Вместо того, чтобы выражать корни уравнения через a a a , подставим x = 5 x=5 x = 5 в уравнение. Чему равно a a a ?

При некоторых значениях параметра уравнение может не иметь решений. Когда корень уравнения выражается через параметр, важно следить за тем, при каких значениях параметра это выражение действительно является корнем. Все преобразования (при раскрытии корня, избавлении от логарифма и т.д.) должны быть равносильны:

2. Решите уравнение x = a sqrt=a x

В зависимости от конкретных значений параметра уравнение может иметь разное количество корней. Если мы выразили корень как функцию параметра, то нужно отдельно рассмотреть те значения параметра, при которых эта функция не имеет смысла. Например, функция 4 − a 2 sqrt 4 − a 2

3. Решить уравнение ( a 2 − 1 ) x = a + 1 (a^2-1)x=a+1 ( a 2 − 1 ) x = a + 1 .

Разложив на множители левую часть уравнения, получим ( a + 1 ) ( a − 1 ) x = a + 1 (a+1)(a -1)x=a+1 ( a + 1 ) ( a − 1 ) x = a + 1 . Рассмотрим особые случаи для параметра a a a .

Чему равно решение уравнения при a = − 1 a=-1 a = − 1 ?

Чему равно решение этого уравнения при a = 1 a=1 a = 1 ?

Чему равно решение уравнения при a ≠ 1 aneq 1 a ≠ 1 и a ≠ − 1 aneq -1 a ≠ − 1 ?

Решение: Рассмотреть разные случаи

Видео:9 класс. Алгебра. Уравнение с параметрами.Скачать

Постановка задачи

В заданиях 18 часто встречаются задачи, которые можно свести к следующей формулировке:

Найти значения параметра, при которых уравнение обладает определённым количеством корней, удовлетворяющих заданному условию.

Посвятим остаток данной статьи разбору различных способов решения таких задач.

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

Способы решения

• Перебор;
• Исследование квадратного трёхчлена;
• Рассмотрение параметра как равноправной переменной;
• Графический метод.

Перебор

Некоторые задачи можно свести к перебору отдельных случаев. Например, мы можем найти несколько возможных корней уравнения. Затем для каждого из них определить, при каких значениях параметра они принадлежат ОДЗ и удовлетворяют другим условиям задачи. Обратимся к примеру, приведённому выше:

Объединим два случая, чтобы получить ответ. При каких значениях a a a хотя бы один корень удовлетворяет условиям?

Исследование квадратного трёхчлена

Часто уравнение с параметром удаётся привести к квадратному. В таких задачах нужно найти значения параметра, при которых корни лежат на некотором промежутке. Для решения подобных примеров необходимо произвести анализ расположения корней. Чтобы определить взаимное расположение границ промежутка и корней уравнения, следует воспользоваться следующими утверждениями:

Для использования приведённых выше утверждений не нужно непосредственно вычислять корни уравнения.

Параметр как равноправная переменная

Несмотря на то, что выше параметр рассматривался как фиксированное, но неизвестное число, можно считать его равноправной переменной.

🎥 Видео

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Простейшие уравнения с параметром #2Скачать

Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решают уравнения в России и США!?Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать