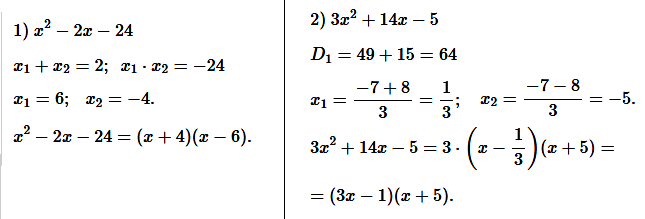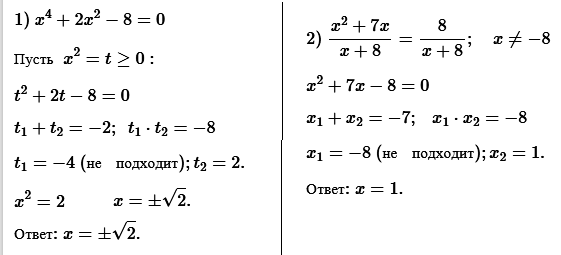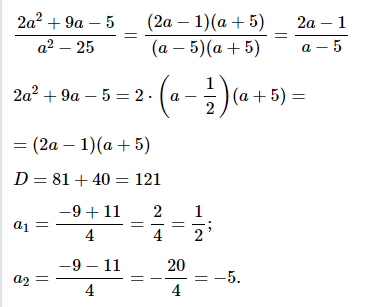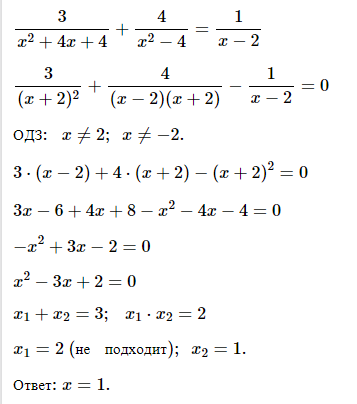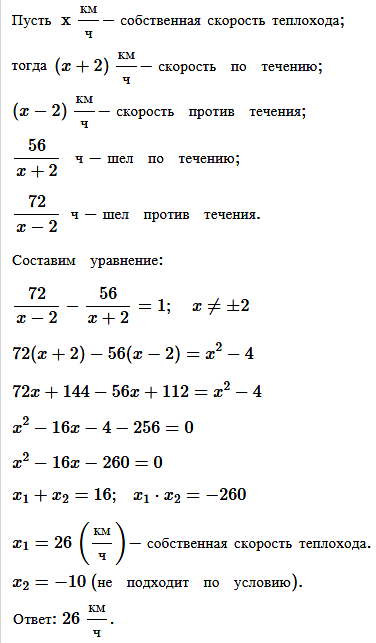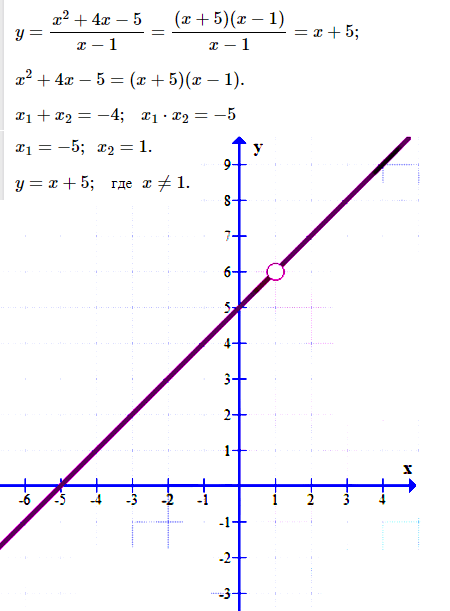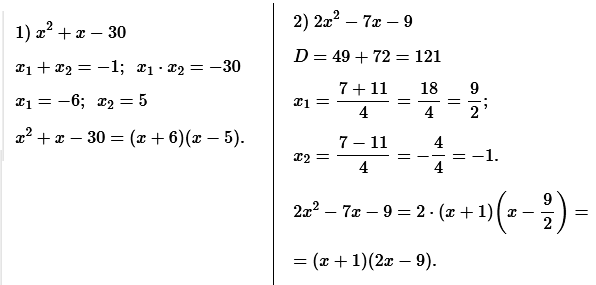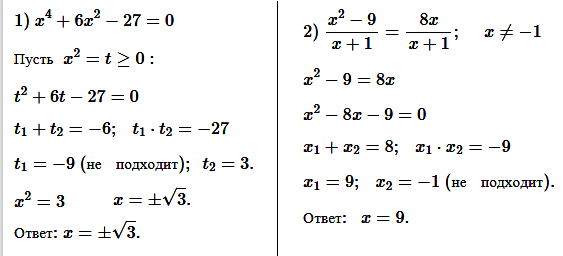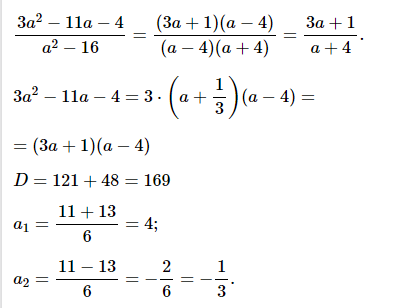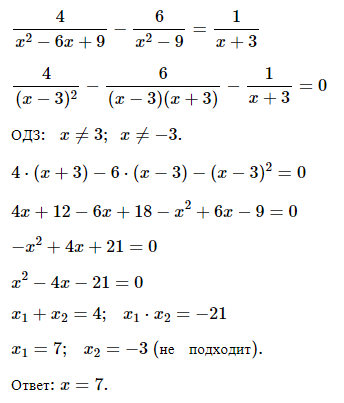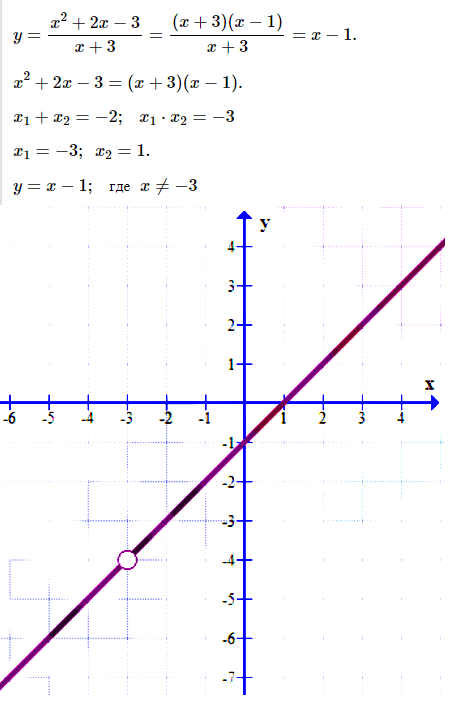Алгебра контрольная работа 8 класс решение задач с помощью рациональных уравнений

Контрольная работа содержит 4 варианта с подробным решением.

Просмотр содержимого документа
«Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»»

В а р и а н т 1

1. Решите уравнение:

а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

В а р и а н т 2

1. Решите уравнение:

а) ; б) = 2.

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч.

В а р и а н т 3

1. Решите уравнение:

а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?

В а р и а н т 4

1. Решите уравнение:

а) ; б) = 2.

2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?

Решение вариантов контрольной работы

В а р и а н т 1

1. а) . Общий знаменатель х 2 – 9.

По теореме, обратной теореме Виета, х₁ = 3; х₂ = –4.

Если х = 3, то х 2 – 9 = 0.

Если х = –4, то х 2 – 9 ≠ 0.

б) = 3. Общий знаменатель х (х – 2).

D = (–17) 2 – 4 · 3 · 10 = 289 – 120 = 169, D 0, 2 корня.

x₁ = = 5;

x₂ = .

Если х = , то х (х – 2) ≠ 0.

О т в е т: а) –4; б) ; 5.

2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 10 мин ( часа) меньше, составим уравнение:

– = . Общий знаменатель 6х (х – 3).

D = (–45) 2 – 4 · 486 = 81, D 0, 2 корня.

x₁ = = 27;

x₂ = = 18.

Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

О т в е т: 18 км/ч.

В а р и а н т 2

1. а) . Общий знаменатель х 2 – 16.

По теореме, обратной теореме Виета х₁ = 4; х₂ = –1.

Если х = 4, то х 2 – 16 = 0.

Если х = – 1, то х 2 – 16 ≠ 0.

б) = 2. Общий знаменатель х (х – 5).

D = (–21) 2 – 4 · 2 · 40 = 441 – 320 = 121, D 0, 2 корня.

x₁ = = 8;

О т в е т: а) –1; б) 2,5; 8.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 3) км/ч, по течению – (х + 3) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

12х 2 + 36х + 5х 2 – 15х – 18х 2 + 162 = 0;

D = (–21) 2 – 4 · 162 = 441 + 648 = 1089, D 0, 2 корня.

Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи.

О т в е т: 27 км/ч.

В а р и а н т 3

1. а) . Общий знаменатель х 2 – 1.

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –1.

Если х = 5, то х 2 – 1 ≠ 0.

Если х = –1, то х 2 – 1 = 0.

б) = 3. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 4; х₂ = –2.

О т в е т: а) 5; б) –2; 4.

2. Пусть х км/ч – скорость, с которой велосипедист ехал из А в В, тогда (х + 4) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение:

– = 1. Общий знаменатель х (х + 4).

Ни один из корней не обращает знаменатель в нуль, но корень х = –12 не удовлетворяет условию задачи.

О т в е т: 16 км/ч.

В а р и а н т 4

1. а) . Общий знаменатель х 2 – 4.

По теореме, обратной теореме Виета, х₁ = 7; х₂ = –2.

Если х = 7, то х 2 – 4 ≠ 0.

Если х = –2, то х 2 – 4 = 0.

б) = 2. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –3.

О т в е т: а) 7; б) –3; 5.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 2) км/ч, по течению – (х + 2) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

15х 2 + 30х + 6х 2 – 12х – 22х 2 + 88 = 0;

Ни один из корней не обращает знаменатель в нуль, но корень х = –4 не удовлетворяет условию задачи.

Видео:Решение задач с помощью рациональных уравнений. Видеоурок 20. Алгебра 8 классСкачать

Мерзляк 8 класс Контрольная 6 Варианты 3-4

Контрольная работа «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений» по алгебре в 8 классе с ответами для УМК Мерзляк, Полонский, Якир. Методическое пособие. Алгебра. Мерзляк 8 класс Контрольная 6 Варианты 3-4.

Видео:Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Алгебра 8 класс (УМК Мерзляк)
Контрольная работа № 6

по теме «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений»

Варианты 1 и 2 этой же контрольной работы № 6 смотрите тут:

Решения и Ответы на Вариант 3

№ 1. Разложите на множители квадратный трёхчлен: 1) x 2 – 2x – 24; 2) 3x 2 + 14x – 5.
ОТВЕТ:

№ 2. Решите уравнение: 1) x 4 + 2x 2 – 8 = 0; 2) (x 2 + 7x)/(x + 8) = 8/(x + 8).
ОТВЕТ:

№ 3. Сократите дробь 1) (2a 2 + 9a – 5)/(a 2 – 25).
ОТВЕТ:

№ 4. Решите уравнение 3/(x 2 + 4x + 4) + 4/(x 2 – 4) = 1/(x – 2).
ОТВЕТ:

№ 5. Теплоход прошёл 72 км против течения реки и 56 км по течению, затратив на путь против течения на 1 ч больше, чем на путь по течению. Найдите собственную скорость теплохода, если скорость течения реки составляет 2 км/ч.
ОТВЕТ: 26 км/ч.

№ 6. Постройте график функции у = (x 2 + 4 x – 5)/(x – 1).

Решения и Ответы на Вариант 4

№ 1. Разложите на множители квадратный трёхчлен: 1) x 2 + x – 30; 2) 2x 2 – 7x – 9.
ОТВЕТ:

№ 2. Решите уравнение: 1) x 4 + 6x 2 – 27 = 0; 2) (x 2 – 9)/(x + 1) = 8x/(x + 1).
ОТВЕТ:

№ 3. Сократите дробь (3a 2 – 11a – 4)/(a 2 – 16).
ОТВЕТ:

№ 4. Решите уравнение 4/(x 2 – 6x + 9) – 6/(x 2 – 9) = 1/(x + 3).
ОТВЕТ:

№ 5. Катер прошёл 64 км против течения реки и 38 км по течению, затратив на путь по течению на 1 ч меньше, чем на путь против течения. Найдите собственную скорость катера, если скорость течения реки составляет 3 км/ч.
ОТВЕТ: 22 км/ч.

№ 6. Постройте график функции у = (x 2 + 2 x – 3)/(x + 3).

Варианты 1 и 2 этой же контрольной работы № 6 смотрите тут:

Вы смотрели: Контрольную работу «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений» по алгебре в 8 классе с ответами для УМК Мерзляк, Полонский, Якир. Методическое пособие. Алгебра. Мерзляк 8 класс Контрольная 6 Варианты 3-4.

(с) Цитаты из пособия «Алгебра 8 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Алгебра 8 класс (Урок№32 - Решение задач с помощью рациональных уравнений.)Скачать

ГДЗ дидактические материалы по алгебре 8 класс Потапов, Никольский, Шевкин Задание: Вариант 1

1. Решите уравнение

2. Решите уравнение

3. Два велосипедиста выезжают одновременно из пункта A и направляются в пункт B, удаленный от A на 90 км. Скорость первого велосипедиста на 1 км/ч больше скорости второго, поэтому первый велосипедист прибыл в B на 1 ч раньше второго. Какова скорость каждого велосипедиста?

4. Решите уравнение

5. Решите уравнение, если известно, что один из его корней равен 3.

📸 Видео

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Алгебра 8. Урок 14 - Задачи на составление дробно-рациональных уравнений (Часть 3)Скачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Решение задач с помощью рациональных уравненийСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

8 класс Решение задач с помощью рациональных уравнений.Скачать

Алгебра 8. Урок 13 - Задачи на составление дробно-рациональных уравнений (Часть 2)Скачать

8 класс. Применение дробных рациональных уравнений. Решение задач. Контрольная работа. Ершова А.П.Скачать

Решение задач с помощью рациональных уравнений (урок 1))Скачать

Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

решение задач с помощью рациональных уравнений 8 класс алгебра № 619Скачать

Рациональные уравнения как математические модели реальных ситуаций - алгебра 8 классСкачать

Алгебра 8. Решение задач с помощью рациональных уравненийСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Алгебра 8 класс. Контрольная работа 6. По учебнику МакарычеваСкачать