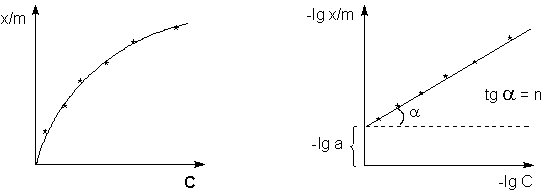ПРАКТИКУМ ПО ФИЗИЧЕСКОЙ И КОЛЛОИДНОЙ ХИМИИ
для студентов биолого-почвенного факультета
Работа № 6
АДСОРБЦИЯ УКСУСНОЙ КИСЛОТЫ НА АКТИВИРОВАННОМ УГЛЕ
Задания к работе
1. Приготовить серию растворов уксусной кислоты с заданными концентрациями.
2. Определить равновесную концентрацию при адсорбции на активированном угле для каждого из растворов.
3. Построить графики изотермы адсорбции в обычных и логарифмических координатах.
4. Определить коэффициенты уравнения Фрейндлиха.
В шести пронумерованных конических колбах объемом 250 мл разбавлением 0.8 М раствора уксусной кислоты готовят рабочие растворы СН3СООН в соответствии с указанным преподавателем номером задания (табл. 1).
Для приготовления растворов при помощи мерного цилиндра (с точностью до 1 мл) наливают в каждую колбу рассчитанное по формуле (1) количество 0.8 М раствора уксусной кислоты и доливают необходимое количество дистиллированной воды.
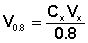
Здесь Сx и Vx — концентрация и объем приготовляемого раствора;
V0.8 — необходимый объем 0.8 М раствора СН3СООН.
Номер задания
Приблизительная концентрация приготовляемых растворов, моль/л
1
2
3
4
5
6
0.01
0.01
0.01
0.01
0.02
0.02
0.02
0.02
0.03
0.03
0.04
0.03
0.04
0.05
0.06
0.07
0.08
0.08
0.08
0.10
0.12
0.15
0.16
0.12
0.16
0.20
0.24
0.30
0.32
0.25
0.32
0.40
0.36
0.40
0.40
0.40
Объём, мл
Точную концентрацию приготовленных растворов определяют титрованием 0.1 М раствором NаОН. Для этого в колбы из второго комплекта с соответствующим номером отбирают из колб №№ 1-3 по 50 мл, из колбы № 4 — 25 мл, из колбы № 5 — 10 мл и из колбы № 6 — 5 мл раствора (т.е. такое количество, чтобы во всех колбах оставалось по 100 мл раствора). После титрования точную концентрацию приготовленных растворов вычисляют по формуле (2):
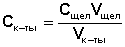
Здесь Сщел и Vщел — концентрация и объем раствора щелочи, затраченного на титрование пробы;
Vк-ты — объем пробы, взятой для титрования.
В каждую из колб со 100 мл раствора вносят указанное преподавателем количество растертого в ступке активированного угля, энергично перемешивают и оставляют на 30 минут, в течении которых содержимое колб периодически взбалтывают (это время можно использовать для титрования отобранных проб). По истечении получаса растворы профильтровывают через складчатые фильтры (первую порцию фильтрата необходимо отбросить, чтобы устранить погрешность, вносимую адсорбцией кислоты на фильтровальной бумаге и разбавлением раствора остающимися в колбе каплями воды). Из фильтрата отбирают пробы такого же объема, что и ранее, титруют их раствором щелочи и рассчитывают концентрацию растворов кислоты после адсорбции.
По формуле (6.3) вычисляют х — количество миллимолей уксусной кислоты, адсорбированной активированным углем и рассчитывают величину удельной адсорбции x/m (m — масса активированного угля) для каждого из растворов.
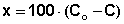
Здесь Со — концентрация исходного раствора;
С — концентрация раствора после адсорбции.
Адсорбция уксусной кислоты на активированном угле описывается уравнением Фрейндлиха:
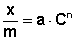
После логарифмирования выражения (4) получается линейная функция (5):
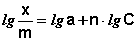
Рисунок 1. Изотерма адсорбции
Рисунок 2. Изотерма адсорбции
в логарифмических координатах.
Полученные данные заносят в таблицу 1 и строят на миллиметровой бумаге изотерму адсорбции, откладывая по оси абсцисс концентрации растворов после адсорбции С, а по оси ординат — значения удельной адсорбции (рис.1).
Для определения коэффициентов в эмпирическом уравнении Фрейндлиха (4) строят изотерму адсорбции в логарифмических координатах (рис. 2). При этом отрезок, отсекаемый на оси ординат, равен lg a, а тангенс угла наклона прямой к оси абсцисс — показателю степени n.
Видео:Лабораторная работа 3. Кинетика адсорбции уксусной кислоты на активированном углеСкачать

Отчет по лабораторной работе Изучение адсорбции уксусной кислоты на активированном угле
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
и аналитической химии
ИЗУЧЕНИЕ АДСОРБЦИИ УКСУСНОЙ КИСЛОТЫ НА АКТИВИРОВАННОМ УГЛЕ
Цель работы: ________________________________________
Адсорбция – это _____________________________________________
Абсолютная адсорбция – это___________________________________
Гиббсовская адсорбция – это__________________________________
Уравнение изотермы мономолекулярной адсорбции Лэнгмюра:
где: А∞ — ____________________________________________________
Изотерма мономолекулярной адсорбции Лэнгмюра:
Уравнение адсорбции Лэнгмюра в линейной форме:
Эмпирическое уравнение адсорбции Фрейндлиха:
где: β — ______________________________________________________

Изучение адсорбции уксусной кислоты из ее водных растворов на активированном угле с использованием титриметрического метода определения концентраций
1. Приготовление растворов уксусной кислоты следующих концентраций: 0,6 М, 0,4 М, 0,3 М, 0,2 М, 0,1 М, 0,05 М.
2. Проведение процесса адсорбции.
3. Определение точной концентрации приготовленных растворов уксусной кислоты методом титрования.
Точную концентрацию приготовленных растворов уксусной кислоты рассчитывают по формуле:

где: 



Результаты титрования приготовленных растворов уксусной кислоты до адсорбции
Исходный раствор титруемой кислоты, моль/л
Объем аликвоты кислоты, взятой для титрования (
Объем щелочи, пошедший на титрова-ние, мл
Среднее значение объема щелочи 
Рассчитанная концентрация кислоты до адсорбции (
Видео:Адсорбция. Простой эксперимент дома / ХимХопСкачать

Изучение адсорбции уксусной кислоты на активированном угле — файл n1.doc
приобрести
Изучение адсорбции уксусной кислоты на активированном угле
скачать (170 kb.)
Доступные файлы (1):
| n1.doc | 170kb. | 22.08.2012 20:15 | скачать |
Видео:Изучение адсорбции уксусной кислоты из водного раствора на активированном углеСкачать

n1.doc
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
Томский политехнический университет
Направление (специальность): Химическая технология и биотехнология
Кафедра: Физической и аналитической химии
Лабораторная работа №3
по курсу «Поверхностные явления и дисперсные системы»
Изучение адсорбции уксусной кислоты
на активированном угле
Студент гр. ФФФ ФФФ.
Руководитель
канд. хим. наук, доц. ФФФФ.
Томск 2009
Цель работы:
1. Изучить процесс адсорбции на границе твердое тело-раствор на примере адсорбции уксусной кислоты на активированном угле
2. Сравнить изотерму адсорбции, полученную экспериментально с изотермами адсорбции, рассчитанными по уравнениям Фрэйндлиха и Лэнгмюра.
Теоретическая часть.
- Адсорбция. Основные понятия и определения
Поверхностная энергия любой термодинамической системы стремится самопроизвольно уменьшиться. Это выражается в уменьшении или площади межфазной поверхности, или поверхностного натяжения. К явлениям, происходящим вследствие стремления к самопроизвольному снижению поверхностного натяжения, относится адсорбция.
На любой границе раздела фаз существует так называемый «поверхностный слой» – переходная область от одной объемной фазы к другой. Поверхностный слой имеет очень малую толщину (всего несколько молекул), но в нем сосредоточен весь избыток поверхностной энергии и массы вещества.
Адсорбция – процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой, т.е. поглощение одного вещества поверхностью другого.
В однокомпонентных системах при формировании поверхностного слоя происходит изменение его структуры (сгущение, уплотнение), которые часто называют автоадсорбцией. В многокомпонентных системах при перераспределении компонентов в поверхностный слой предпочтительнее переходит тот компонент, который сильнее уменьшает межфазное (поверхностное) натяжение.
Если поглощаемое вещество диффундирует вглубь поглотителя и распределяется по всему объему, то такое явление называют абсорбцией (поглощение объемом).
Адсорбент – вещество, на поверхности которого идет адсорбция. Адсорбат – вещество, адсорбированное поверхностью адсорбента. Адсорбтив – вещество, находящееся в объемной фазе, способное к адсорбции.
С термодинамической точки зрения адсорбция — самопроизвольный процесс выравнивания химических потенциалов компонента в объеме системы и поверхностном слое. Этот процесс происходит вследствие стремления к минимуму поверхностной энергии или энергии Гиббса системы.
- Количественные способы выражения адсорбции
Количественно величину адсорбции выражают двумя способами:
- Абсолютная адсорбция (А) – количество вещества (моль) в поверхностном слое, приходящееся на единицу площади поверхности или единицу массы адсорбента (моль/м 2 , моль/г).

где: CS – концентрация компонента в поверхностном слое объемом
h – толщина поверхностного слоя.
Гиббсовская (избыточная) адсорбция (Г) – избыточное число моль адсорбата в поверхностном слое (на единицу площади поверхности) по сравнению с тем числом моль, который бы находился в адсорбционном объеме в отсутствии адсорбции.

где: Nобщ – общее число моль адсорбтива;
СV – равновесная объемная концентрация адсорбтива;
S – площадь поверхности адсорбента;
С0 – исходная концентрация адсорбтива;
CS – концентрация адсорбата в поверхностном слое.
При больших избытках адсорбата в поверхностном слое (СS>>CV), равновесной концентрацией адсорбтива в объеме фазы (CV) можно пренебречь, поэтому величины А и Г приблизительно равны.
При экспериментальном определении величину адсорбции рассчитывают по разности исходных и равновесных концентраций адсорбтива, т.е. определяют величину Г.

где: C0 – концентрация адсорбтива до адсорбции;
Ср – равновесная концентрация адсорбтива после адсорбции,
S – площадь межфазной поверхности,
V – объем раствора.
Если адсорбентом является твердое пористое тело, общую поверхность которого определить невозможно, то адсорбцию Г относят к единице массы адсорбента (моль/г).
3. Теория мономолекулярной адсорбции Лэнгмюра
В настоящее время не создано общей теории, которая бы достаточно корректно описывала бы все виды адсорбции на различных поверхностях раздела фаз. Рассмотрим основные положения «классической» теории адсорбции, разработанной в начале XX века Лэнгмюром:
- Адсорбция молекул адсорбата происходит на активных центрах, всегда существующих на поверхности адсорбента. Активные центры адсорбента энергетически равноценны.
- Каждый активный центр может адсорбировать только одну молекулу адсорбата. В результате этого на поверхности адсорбента образуется мономолекулярный слой адсорбата.
- Адсорбированные молекулы не взаимодействуют друг с другом. Поэтому время пребывания молекул на активных центрах не зависит от того, заняты молекулами соседние активные центры или нет.
- Адсорбция носит динамический характер. Адсорбат удерживается на поверхности адсорбента некоторое время, а потом десорбируется.
На основе приведенных исходных положений Лэнгмюром было предложено уравнение изотермы мономолекулярной адсорбции, которое для адсорбции из растворов имеет вид:

где: С – равновесная концентрация адсорбтива;
К – константа адсорбционного равновесия, характеризующая энергию взаимодействия адсорбата и адсорбента;
А? – предельная адсорбция (емкость адсорбционного монослоя).
Типичный вид изотермы Лэнгмюра показан на рисунке 1.
Рис.1. Изотерма мономолекулярной адсорбции Лэнгмюра в координатах А=f(С).
На изотерме адсорбции Лэнгмюра выделяют три участка:
I — область малых концентраций (КС >1), тогда: А=А?, вся поверхность адсорбента занята молекулами адсорбата.
II – область средних концентраций: расчет ведут по уравнению (4).
3.1. Расчет констант уравнения Лэнгмюра
Константы (К и А?) уравнения Лэнгмюра рассчитывают двумя способами:
1. Аналитический способ: в уравнение (4) подставляют экспериментальные значения А при соответствующих значения С, решают систему уравнений с двумя неизвестными, находят А? и К.
2. Графический способ: уравнение (4) приводят к линейному виду: y=a+bx.

Строят изотерму адсорбции в координатах линейной формы уравнения Лэнгмюра (рис.2):
Рис.2. Изотерма адсорбции в координатах линейной формы уравнения Лэнгмюра.
Экстраполяция зависимости до оси ординат дает отрезок, равный 

Уравнение Лэнгмюра, выведенное для описания процесса адсорбции газа на твердой поверхности, используют и для описания молекулярной адсорбции из растворов.
4. Эмпирическое уравнение адсорбции Фрейндлиха
Для описания процесса адсорбции также используют эмпирическое уравнение Фрейндлиха.

где: С – равновесная концентрация адсорбтива;
? и n – константы, определяемые опытным путем.
Константа ? по своему физическому смыслу представляет собой значение адсорбции при равновесной концентрации адсорбтива, равной единице (при С=1, А = ?). Эта константа для различных адсорбционных систем колеблется в пределах 2 ч 2,5.
Показатель 

Константы уравнения Фрейндлиха из опытных данных определяют графически. Для этого уравнение (6) логарифмируют:

Уравнение (7) представляет собой уравнение прямой в координатах 
Рис.3. График для нахождения констант в уравнении Фрейндлиха
Экстраполяция зависимости до оси ординат дает отрезок, равный lg ?, тангенс угла наклона прямой равен 
Таблица 1. Результаты титрования исходных растворов уксусной кислоты до адсорбции
| Раствор кислоты, концентрация которого проверяется, моль/л | Объем кислоты, взятый на титрование (Vк), мл | Объем щелочи, пошедший на титрование, мл | Среднее значение объема щелочи (Vщ), мл | Рассчитанная концентрация кислоты, моль/л |
| 0,6 | 2 | 14,5 14,3 | 14,30 | 0,71 |
| 0,4 | 2 | 9,5 9,6 | 9,53 | 0,47 |
| 0,3 | 5 | 24,8 24,7 | 24,67 | 0,49 |
| 0,2 | 5 | 16,2 16,3 | 16,23 | 0,32 |
| 0,1 | 5 | 9,5 9,6 | 9,43 | 0,19 |
| 0,05 | 5 | 4,6 4,4 | 4,5 | 0,09 |
Таблица 2. Результаты титрования растворов уксусной кислоты после адсорбции
| Раствор титруемой кислоты моль/л | Объем кислоты, взятый на титрование (Vк), мл | Объем щелочи, пошедший на титрование, мл | Среднее значение объема щелочи (Vщ), мл | Рассчитанная концентрация кислоты, моль/л |
| 0,71 | 2 | 11,2 11,2 | 11,13 | 0,56 |
| 0,47 | 2 | 6,6 6,7 | 6,67 | 0,33 |
| 0,49 | 5 | 15,6 15,5 | 15,63 | 0,31 |
| 0,32 | 5 | 5,7 5,7 | 5,73 | 0,11 |
| 0,19 | 5 | 2,6 2,6 2,6 | 2,6 | 0,05 |
| 0,09 | 5 | 0,8 0,7 | 0,6 | 0,01 |
Таблица 3.
| № | Ci равн, моль/л | Гi эксп, ммоль/г | Сi/Гi, г/л | Ai (Лэнгмюр), ммоль/г | Ai (Фрэйндлих), ммоль/г | lgГi эксп | lgСi равн |
| 1 | 0,71 | 7,5 | 94,66667 | 7,83 | 11,65 | 0,875061 | 2,851258 |
| 2 | 0,47 | 7 | 67,14286 | 7,64 | 10,40 | 0,845098 | 2,672098 |
| 3 | 0,49 | 9 | 54,44444 | 7,66 | 10,52 | 0,954243 | 2,690196 |
| 4 | 0,32 | 10,5 | 30,47619 | 7,39 | 9,36 | 1,021189 | 2,50515 |
| 5 | 0,19 | 7 | 27,14286 | 6,92 | 8,11 | 0,845098 | 2,278754 |
| 6 | 0,09 | 4 | 22,5 | 5,88 | 6,60 | 0,60206 | 1,954243 |
Расчет по Лэнгмюру

Расчет по Фрэйндлиху
При выполнении работы был изучен процесс адсорбции уксусной кислоты на активированном угле. По результатам экспериментальных данных были построены изотермы адсорбции по Лэнгмюру и Фрэйндлиху. Изотерма по Лэнгмюру более схожа с экспериментальной.
🔥 Видео
Адсорбция на твёрдой поверхностиСкачать

Адсорбция. Как очистить воду при помощи активированного угля.Скачать

Изучение явления адсорбцииСкачать

5.1. Адсорбция. Классификация адсорбцииСкачать

Лабораторная работа Исследование процессов адсорбции активированным углем различных веществСкачать

Адсорбция на поверхностях растворовСкачать

Адсорбция Активированный угольСкачать

Адсорбция из растворов на твердой поверхности (лабораторная работа 2)Скачать

Лабораторная работа №16. Свойства уксусной кислоты. 9 класс.Скачать

АдсорбцияСкачать

Практическое занятие 4. Адсорбция на границе твердое тело – газСкачать

Активированный уголь. Опыты с детьми. Точка Гравитиции.Скачать

Поверхностные явления. Адсорбция.Скачать

АдсорбцияСкачать

АДСОРБЦИОННЫЕ СВОЙСТВА АКТИВИРОВАННОГО УГЛЯ И СИЛИКАГЕЛЯСкачать

Взаимодействие уксусной кислоты с металламиСкачать

Только так можно убрать инсулинорезистентность, метаболический синдром и сахарный диабет 2 типа!Скачать