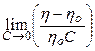Окклюзия — поглощение газов металлами (сплавами) или их расплавами с образов, растворов или химических соединений (оксидов, нитридов, гидридов и т.п.). При окклюзии газы поглощаются не поверхностным слоем, а всем объемом поглотителя, подобно абсорбции (растворению) газов в жидкостях. При окклюзии в отличие от поверхностной адсорбции примеси поглощаются по всей массе осадка внутри его кристаллов.
Наиболее, характерна окклюзия газов, например Н2, металлами VIII группы Периодической системы элементов. Так, при комнатной температуре 1 объём иридия поглощает более 800, а палладия — более 700 объёмов водорода. Окклюдированный газ даёт с металлами твёрдый раствор; иногда часть поглощённого газа образует с ними химические соединения (гидриды, нитриды и др.).
Твёрдое тело, поглощающее газ, называют сорбентом (адсорбентом, абсорбентом). Газ или пар, поглощаемый сорбентом, называют сорбатом (адсорбатом, абсорбатом).
Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Капиллярная конденсация
Капиллярная конденсация — сжижение пара в капиллярах, щелях или порах в твердых телах. Капиллярная конденсация обусловлена наличием у адсорбента мелких пор. Пары адсорбтива конденсируются в таких порах при давлениях, меньших давления насыщенного пара над плоской поверхностью вследствие образования в капиллярах вогнутых менисков. Возникновение этих менисков следует представлять как результат слияния жидких слоев, образовавшихся на стенках капилляра вследствие адсорбции паров. Возникновение вогнутых менисков возможно только в том случае, если образовавшаяся жидкость смачивает стенки капилляра.
Явление конденсации отлично от физической адсорбции. Элементарная теория капиллярной конденсации не учитывает специфического действия поверхностных сил. Адсорбция может происходить на плоских поверхностях, тогда как капиллярная конденсация в таких условия невозможна.
Для расчета изотерм капиллярной конденсации используют модельные системы — решеточные системы, упаковки из частиц правильной формы. Чаще уравнения капиллярной конденсации используют для решения обратной задачи, то есть определяют размеры пор и их распределение по размерам на основании изотерм, с привлечением модельных представлений о геометрии порового пространства. Капиллярная конденсация может наблюдаться не только в системах жидкость-пар, но и в промерзающих пористых телах при наличии прослоек незамерзающей воды на внутренней поверхности пор.
Большую роль капиллярная конденсация играет также в процессах сушки, удерживания влаги почвами и другими пористыми материалами. Отрицательное капиллярное давление может удерживать вместе смачиваемые жидкостью частицы, обеспечивая прочность таких структур. В случае несвязных пористых тел возможна их объемная деформация под действием капиллярных сил — так называемая капиллярная контракция. Капиллярная конденсация может быть причиной прилипания частиц пыли к твердым поверхностям, разрушения пористых тел при замораживании сконденсированной жидкости в порах. Для уменьшения эффекта капиллярной конденсации используют лиофобизацию поверхности пористых тел.
Задачи [8, стр. 70-75]
1. Вычислить степень адсорбции фенола на поверхности капель эмульгированного масла по экспериментальным данным зависимости поверхностного натяжения водного раствора фенола от его концентрации:
Видео:5.3. Адсорбция на границе жидкость-газ. Поверхностно активные вещества ПАВСкачать

Адсорбционная теория Ленгмюра
Для описания изотермы по рис. 2.10а используют уравнения вида:
где К и к—константы.
Приведенные уравнение являются основными в теории мономолеку- лярной адсорбции Ленгмюра. Чаще используется первый вариант, так как в случае адсорбции ПАВ справедливы все уравнения, содержащие величину А, поскольку при этом абсолютная и гиббсовская адсорбции практически одинаковы ( А = Г).
При выводе уравнения Ленгмюра физическое взаимодействие на поверхности может быть представлено как квазихимическая реакция:
где А — адсорбционные центры поверхности; В— распределяемое вещество; АВ — комплекс, образующийся на поверхности.
По мерс увеличения концентрации (давления) вещества В равновесие реакции сдвигается в сторону образования комплекса и свободных центров становится меньше. Константа адсорбционного равновесия по закону действия масс имеет вид:
Введем обозначения: 
центров, приходящихся на единицу площади поверхности или единицу массы адсорбента. Если А — величина предельной адсорбции (емкость адсорбционного монослоя), то 

Для газов вместо концентрации используется давление д (так как концентрация газов и паров при газовой адсорбции практически пропорциональна парциальным давлениям):
Для характеристики адсорбции используется степень заполнения поверхности 
можно записать в виде
Константы адсорбционного равновесия в разных видах уравнений Ленгмюра (К, к и к’) характеризуют энергию взаимодействия адсорбента и адсорбата: чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия.
Известен другой вариант вывода уравнения Ленгмюра — кинетический, в котором основное внимание уделяется скорости наступления динамичного равновесия процессов адсорбции и десорбции. При этом выводе показывается, что константа адсорбционного равновесия равна отношению констант скорости адсорбции и десорбции:
Для анализа изотермы адсорбции по уравнению Ленгмюра воспроизведем типичную изотерму адсорбции по мономолекулярному механизму (рис. 2.26).
Рис. 2.26. Изотерма мономолекулярной адсорбции
Анализ изотермы мономолекулярной адсорбции:
— при очень малых концентрациях, когда с^О, произведением К с в знаменателе можно пренебречь, поэтому получаем А = АСС-Кс или А = КГ‘С. Полученные соотношения соответствуют закону Генри и коэффициент пропорциональности Кг — константа Генри. По закону Генри
величина адсорбции с ростом концентрации на участке АВ увеличивается линейно;
— при больших концентрациях или давлениях, когда произведение К-с» 1, адсорбция стремится к предельному значению А = А#. Это соотношение на участке СД отвечает состоянию насыщения поверхности адсорбента молекулами адсорбата, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата;
в области средних концентраций на участке ВС уравнение Ленгмюра применимо в полной форме.
Физический смысл константы Генри, иногда называемый еще константой распределения, поясняют следующие рассуждения. Если поверхностный слой рассматривать как отдельную фазу, то перераспределение вещества между поверхностным слоем и объемом фазы будет происходить до тех пор, пока химические потенциалы обеих фаз не станут равными:
где ps — химический потенциал в поверхностном слое; pv— химический потенциал объемной фазы.
Учитывая, что 

Если в области малых концентраций активности считать равными концентрациям, то поверхностная концентрация равна адсорбции
as = сs = А и тогда 
чается уравнение Генри: А = Кр-с.
Можно получить подобное выражение через давление, учитывая, что в области малых концентраций газ подчиняется закону состояния идеального газа pV = nRT, откуда 
нее соотношение в уравнение адсорбции, получаем:
Уравнения Генри просты по виду, но иногда их бывает вполне достаточно для практических расчетов. На твердых поверхностях область действия этого закона мала из-за неоднородности поверхности. Но даже на однородной поверхности обнаруживается отклонение от линейной зависимости при увеличении концентрации (давления). Это объясняется уменьшением доли свободной поверхности, приводящим к замедлению роста адсорбции.
Отклонения от закона Генри учитывает эмпирическое уравнение, установленное Фрейндлихом и Бедекером на основе изучения адсорбции газов на твердых адсорбентах. Позднее это уравнение было теоретически обосновано Зельдовичем и оказалось применимым и для растворов.
Теория мономолекулярной адсорбции была создана Ленгмюром при изучении адсорбции газов на твердых поверхностях. Основные положения теории состоят в следующем:
- — на поверхности твердого адсорбента имеются активные центры, все они энергетически однородны (поверхность эквипотенциальна) и их количество на единице площади постоянно для данного адсорбента;
- — каждый активный ценгр удерживает только одну молекулу адсорбата, которая закреплена с ним силами физической природы (адсорбция обратима). Адсорбированная молекула образует с центром прочный комплекс и не способна перемещаться по поверхности;
- — учитываются только силы взаимодействия молекулы с адсорбционным центром (без учета взаимодействия между молекулами адсорбага).
Несмотря на жесткие ограничения, теория широко используется и даст хорошую сходимость с практическими результатами для большого количества видов адсорбции. В настоящее время она распространяется на адсорбцию на других границах раздела.
Теория Ленгмюра объясняет адсорбцию ПАВ на границе вода — воздух, когда полярная группа, обладая большим сродством к полярной фазе, втягивается в воду, в то время как неполярный радикал выталкивается в неполярную фазу (воздух) и при малых концентрациях углеводородные цепи «плавают» на поверхности воды (это возможно из-за их гибкости). С ростом концентрации цепи поднимаются и в насыщенном адсорбционном слое занимают вертикальное положение, при этом поверхность воды сплошь покрыта «частоколом» из вертикально ориентированных молекул ПАВ. Значение поверхностного натяжения в этом случае приближается к значению чистого жидкого ПАВ на границе с воздухом. Максимальная адсорбция Га0 именно поэтому не зависит от длины углеводородного радикала, а определяется только размерами поперечного сечения молекул.
Существование насыщенных адсорбционных слоев позволяет определять размеры молекул ПАВ. Впервые в истории химии размеры молекул были определены именно коллоидно-химическим путем и уже позже подтверждены другими методами. Поскольку в насыщенном слое молекулы плотно упакованы и имеют вертикальную ориентацию, то можно рассчитать важные характеристики мономолекулярного слоя:
— размер поперечного сечения молекул, то есть площадь, занимаемую одной молекулой ПАВ в поверхностном слое («посадочную площадку»):
— длину молекулы ПАВ, равную толщине адсорбционного слоя:
где NА — число Авогадро, р и М — плотность и молекулярная масса поверхностно-активного вещества.
Для определения постоянных параметров проводят преобразование уравнения Ленгмюра к уравнению прямой линии
Представляя экспериментальные данные в обратных осях 




дельной адсорбции, по которому можно вычислить адсорбционную константу К. Во втором случае, наоборот, отрезок на ординате связан с величиной обратной предельной адсорбции 
прямой можно определить 
Рассмотрим вариант определения констант уравнения Ленгмюра на примере адсорбции в системе вода — изоамиловый спирт. В таблице представлены экспериментальные данные но величинам поверхностного натяжения о растворов различной концентрации с:
Видео:Адсорбция на поверхностях растворовСкачать

VII. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ. АДСОРБЦИЯ
Задача 168. Суспензия кварца содержит сферические частицы, причем 30% массы приходится на частицы, имеющие радиус 1·10 — 5 м, а масса остальных – на частицы радиуса 5·10 — 5 м. Какова удельная поверхность кварца?
Задача 169. Определите коэффициент диффузии красителя конго красный в водном растворе, если при градиенте концентрация 0,5 кг/м 3 за 2 ч через 25·10 — 4 м 2 проходит 4,9·10 — 7 г вещества.
Задача 170. Определите радиус частиц золя иодида серебра, используя следующие данные: коэффициент диффузии равен 1,2·10 — 10 м 2 /с. Вязкость среды – 10 — 3 Н·с/м 2 , температура – 298 К.
Задача 171. Золь диоксида кремния в воде содержит частицы, радиус которых равен 2·10 — 8 м. Определите, на какой высоте начального уровня концентрация частиц уменьшается в 2 раза. Для расчетов используйте следующие данные: плотность частиц – 2,1·10 — 3 кг/м 3 , плотность среды – 1·10 — 3 кг/м 3 , температура -298 К.
Задача 172. Рассчитайте среднее квадратичное смещение аэрозольной частицы за 15 с по следующим данным: радиус частицы – 10 — 8 м, вязкость среды – 1,9·10 — 7 Н·с/м 2 , температура – 298 К.
Задача 173. Вычислите удельную поверхность частиц золя золота, полученного в результате дробления 0,5 г золота на частицы шарообразной формы диаметром 7,0·10 — 9 м. Плотность золота ρ = 19320 кг/м 3 .
Задача 174. Золь иодида серебра AgI получен при добавлении к 0,02 л 0,01н раствора KI 0,028 л 0,005 н AgNO3. Определите заряд частиц полученного золя и напишите формулу его мицеллы.
Задача 175. Какой объем 0,002н раствора BaCl2 надо добавить к 0,03 л 0,0006 н. Al2(SO4)3, чтобы получить положительно заряженные частицы золя сульфата бария. Напишите формулу мицеллы золя BaSO4.
Задача 176. Определите, за какое время осядет частица бентонита, находящаяся на поверхности жидкости, если высота столба жидкости равна 0,1 м, вязкость среды – 2·10 — 3 Н·с/м 2 , радиус частицы – 14·10 — 6 м, плотность частицы – 2,1·10 — 3 кг/м 3 , плотность жидкости – 1,1·10 — 3 кг/м 3 . Во сколько раз быстрее осядет эта же частица, если жидкость центрифугировать в пробирке с угловой скоростью 600 с — 1 ? Начальное расстояние частицы от оси вращения –0,15 м, конечное – 0,25 м.
Задача 177. Какова дисперсность частиц талька, если удельная поверхность порошка талька: а) 2·10 2 м 2 /кг; б) 2·10 3 м 2 /кг; в) 2·10 4 м 2 /кг. Плотность талька – 2,7 г/см 3 , частицы порошка имеют сферическую форму. Какой из порошков лучше использовать для кожных присыпок?
Задача 178. . Определите константы уравнения изотермы адсорбции Ленгмюра для растворов гексилового и гептилового спиртов. Выполняется ли правило Дюкло-Траубе в этом случае? Зависимости адсорбции этих соединений от концентрации приводятся в таблице.
| Гексиловый спирт | Гептиловый спирт | ||
| концентрация С·10 3 кмоль/м 3 | адсорбция Г·10 3 кмоль/м 3 | концентрация С·10 3 кмоль/м 3 | адсорбция Г·10 3 кмоль/м 3 |
| 0,935 1,875 3,10 5,5 11,05 | 8,75 17,35 25,1 37,8 56,5 | 0,384 0,50 0,655 1,25 2,60 | 11,1 14,5 18,2 27,8 49,2 |
Задача 179.Зависимость поверхностного натяжения водных растворов амилового спи
рта (С5Н11ОН) от концентрации при 25 о С выражается следующим образом:
| Концентрация, кмоль/м 3 | Поверхностное натяжение, мн/м |
| 72,0 | |
| 0,0019 | 70,4 |
| 0,0038 | 69,2 |
| 0,0075 | 66,7 |
| 0,015 | 61,7 |
| 0,030 | 55,3 |
| 0,060 | 46,6 |
| 0,120 | 38,0 |
Определите графически адсорбцию амилового спирта из раствора с концентрацией 0,030 кмоль/м 3 .
Задача 180. При исследовании адсорбции азота на 1 г активированного угля при 273 К получены следующие результаты (объем поглощенного газа пересчитан к н. у.):
| р, Торр | 4,5 | 9,2 | 18,6 | 40,2 |
| V, см 3 ·г -1 | 1,12 | 2,22 | 4,22 | 8,02 |
Выясните, описываются ли эти данные изотермой Ленгмюра и определите площадь поверхности адсорбента, если в плотном монослое молекула азота занимает площадь 0,162 нм 2 .
Задача 181. При 195 К и парциальном давлении р(Ar) = 24 Торр на 1 г коксового угля адсорбируется некоторое количество аргона. При увеличении давления в 9 раз количество сорбирующегося газа возрастает в 5 раз. Определите степень заполнения поверхности при 195 К и давлении аргона 100 Торр.
Задача 182. При 312 К и давлении 1,21 Торр на поверхности микропористого глинистого адсорбента сорбируется 1,37 моль·кг -1 паров метилового спирта. Такая же адсорбция достигается при повышении температуры до 320 К и увеличении давления до 3,16 Торр. Вычислите энтальпию адсорбции метилового спирта при данной степени заполнения поверхности.
Задача 183. Определить суммарную площадь поверхности частиц, если при дроблении 1 г серы получаются частицы: а) кубической формы с длиной ребра 10 — 5 см; б) частицы шарообразной формы с поперечником 2·10 — 6 см. Плотность серы 2,07 г/см 3 .
Задача 184.Врач ошибочно выписал рецепт на лекарство:
Rp: Strychnini nitratis 0,001
Carbonis activati 0,5
M. f. Pulv. D. t. d. 5
S. По одному порошку через 2 часа,
не учитывая, что активный уголь будет адсорбировать алкалоиды, вследствие чего организм больного не получит необходимой дозы ни противоядия, ни антагониста. Вычислите количество каждого из алкалоидов, адсорбированных 1 г угля, если стрихнина нитрат адсорбируется полностью, а кофеин – на 80%.
Задача 185. Определить число частиц, образующихся при раздроблении 0,2 см 3 ртути на правильные кубики с длиной ребра 8·10 -6 см. Плотность ртути равна 13,546 г/см 3 .
Задача 186. Определить поверхностный избыток (кмоль/м 2 ) при 10 о С для раствора, содержащего 50 мг/л пеларгоновой кислоты С8Н17СООН. Поверхностное натяжение исследуемого раствора 57,0·10 — 3 Н/м. σ 10 Н2О = 74,22·10 -3 н/м.
Задача 187. К 100 см 3 раствора уксусной кислоты различной концентрации при 20 0 С добавили по 3 г активированного угля. Количество кислоты до и после адсорбции определяли титрованием 50 см 3 раствора 0,1н NаОН. Определить соотношение x/m для каждого из растворов, используя данные титрования:
| Объем NаОН, израсходованный на титрование до адсорбции, см 3 | 5,5 | 10,6 | 23,0 |
| Объем NаОН, израсходованный на титрование после адсорбции, см 3 | 1,2 | 3,65 | 10,2 |
Задача 188.По опытным данным, полученным при изучении адсорбции углем бензойной кислоты из раствора ее в бензоле при 25 о С, определить графически константы а и 1/n в уравнении Фрейндлиха:
| С,ммоль/см 3 | 0,006 | 0,025 | 0,053 | 0,118 |
| х/т,ммоль/г | 0,44 | 0,78 | 1,04 | 1,44 |
VIII. КОЛЛОИДНАЯ ХИМИЯ
Задача 189. Определите энергию Гиббса Gs поверхности капель водяного тумана массой m = 4 г при 293 К, если поверхностное натяжение воды σ = 72,7 мДж/м 2 , плотность воды ρ = 0,998 г/см 3 , дисперсность частиц D = 50 мкм — 1 .
Задача 190. Рассчитайте полную поверхностную энергию 5 г эмульсии бензола в воде с концентрацией 75 % (масс.) и дисперсностью D = 2 мкм — 1 при температуре 313 К. Плотность бензола при этой температуре ρ = 0,858 г/см 3 , поверхностное натяжение σ = 32,0 мДж/м 2 , температурный коэффициент поверхностного натяжения бензола dσ/dT = – 0,13 мДж/(м 2 ·К).
Задача 191. Рассчитайте давление насыщенных паров p над каплями воды с дисперсностью D = 0,1 нм — 1 при температуре 293 К. Давление паров воды над плоской поверхностью при этой температуре ps = 2338 Па, плотность воды ρ = 0,998 г/см 3 , поверхностное натяжение воды σ = 72,7 мДж/м 2 .
Задача 192. Две вертикальные параллельные пластинки частично погружены в жидкость на расстоянии d = 1 мм друг от друга. Угол смачивания θ пластинок жидкостью составляет 30 о . Поверхностное натяжение жидкости σ = 65 мДж/м 2 , разность плотностей жидкости и воздуха Δρ = 1 г/см 3 .
Задача 193. В воздухе, содержащем пары воды, образуется туман при температуре 270,8К (коэффициент пресыщения γ равен 4,21). Рассчитайте критический размер ядер конденсации и число молекул, содержащихся в них. Поверхностное натяжение воды σ = 74 мДж/м 2 , мольный объем воды VM = 18·10 -6 м 3 /моль.
Задача 194. Рассчитайте работу адгезии Wa ртути к стеклу при 293 К, если известен краевой угол θ = 130 о . Поверхностное натяжение ртути σ = 475 мДж/м 2 . Найдите коэффициент растекания f ртути по поверхности стекла.
Задача 195.Ниже приведены экспериментальные данные по адсорбции азота на TiO2 (рутиле) при 75 К:
| р·10 — 2 , Па | 60,94 | 116,41 | 169,84 | 218,65 | 272,25 |
| А, моль/кг | 0,367 | 0,417 | 0,467 | 0,512 | 0,567 |
Постройте график, соответствующий линейному уравнению БЭТ. Найдите константы А∞ и С. Рассчитайте удельную поверхность адсорбента. Давление насыщенного пара азота при указанной температуре ps = 78,3·10 3 Па, площадь, занимаемая одной молекулой азота, Sо= 0,16 нм 2 .
Задача 196. Постройте кривую капиллярной конденсации и интегральную кривую распределения пор по размерам для активированного угля, пользуясь экспериментальными данными капиллярной конденсации паров бензола при 293 К:
| р·10 -2 , Па | 19,8 | 29,9 | 39,8 | 59,6 | 79,7 | 89,4 | 98,3 | |
| А, моль/кг | адсорбция | 4,5 | 5,4 | 6,5 | 10,2 | 14,4 | 17,0 | 20,0 |
| десорбция | 4,5 | 6,0 | 9,0 | 13,9 | 17,5 | 19,0 | 20,0 |
При этой температуре для бензола мольный объем VM=89·10 — 6 м 3 /моль, поверхностное натяжение σ = 28,9 мДж/м 2 , давление насыщенного пара ps = 99,3·10 2 Па.
Задача 197. Рассчитайте изостерическую теплоту адсорбции этана на поверхности графитированной сажи (при степени заполнения θ = 1) по следующим данным:
| р, Па | 251,2 | 89,9 | 33,1 | 12,6 |
| Т, К |
Задача 198. Адсорбция растворенного в воде ПАВ на поверхности ртуть – вода подчиняется уравнению Ленгмюра. При концентрации ПАВ 0,2 моль/л степень заполнения поверхности θ = 0,5. Рассчитайте поверхностное натяжение ртути на границе с раствором при 298 К и концентрации ПАВ в растворе 0,1 моль/л. Предельное значение площади, занимаемой молекулой ПАВ на поверхности, Sо = 0,20 нм 2 , поверхностное натяжение ртути на границе с водой равно 0,373 Дж/м 2 .
Задача 199. Ниже приведены значения поверхностного давления π валериановой кислоты при 292К при различной площади поверхности, приходящейся на 1 моль кислоты:
| π·10 2 , Н/м | 0,35 | 0,53 | 0,78 | 1,10 | 1,49 | 1,92 | 2,36 | 2,85 | 3,36 |
| SM·10 — 5 , м 2 /моль | 6,92 | 4,66 | 3,49 | 2,77 | 2,44 | 2,27 | 2,11 | 2,03 | 1,89 |
Известно, что поверхностное давление раствора валериановой кислоты с концентрацией 4 ммоль/л равно 0,002 Н/м. Рассчитайте константы уравнения Шишковского.
Задача 200. Полистирольный сульфокатионит в Н + -форме в количестве m = 1 г внесли в раствор KСl с исходной концентрацией Со = 100 экв/м 3 объемом V = 50 мл и смесь выдержали до равновесного состояния. Рассчитайте равновесную концентрацию калия в ионите, если константа ионообменного равновесия KK + /Н + = 2,5, а полная обменная емкость катионита ПОЕ = 5 экв/кг.
Задача 201. Определите коэффициент диффузии D и средне-квадратичный сдвиг Δ частицы гидрозоля за время τ = 10 с, если радиус частицы r = 50 нм, температура опыта 293 К, вязкость среды η = 10 -3 Па·с.
Задача 202. Определите радиус частиц гидрозоля золота, если после установления диффузионно-седиментационного равновесия при 293 К на высоте h = 8,56 см концентрация частиц изменяется в е раз. Плотность золота ρ = 19,3 г/см 3 , плотность воды ρ0 = 1,0 г/см 3 .
Задача 203 Рассчитайте осмотическое давление 30%-ного (масс.) гидрозоля SiO2 при 293 К, если удельная поверхность частиц Sуд = 2,7·10 5 м 2 /кг. Плотность частиц гидрозоля ρ = 2,2 г/см 3 , плотность среды ρ0 = 1,15 г/см 3 .
Задача 204. Частицы бентонита дисперсностью D = 0,8 мкм — 1 оседают в водной среде под действием силы тяжести. Определите время оседания τ1 на расстояние h = 0,1 м, если плотность бентонита ρ = 2,1 г/см 3 , плотность среды ρ0 = 1,1 г/см 3 , вязкость среды η = 2·10 — 3 Па·с. Во сколько раз быстрее осядут частицы на то же расстояние в центробежном поле, если начальное расстояние от оси вращения х0 = 0,15 м, а скорость вращения центрифуги n = 600 об/с.
Задача 205. Рассчитайте электрокинетический потенциал на границе водный раствор – пористая стеклянная мембрана по данным электроосмоса: сила тока I = 3·10 -3 А, за время 60 с переносится 0,63 мл раствора, вязкость дисперсионной среды η = 10 — 3 Па·с, относительная диэлектрическая проницаемость среды ε = 80,1. Электрическое сопротивление мембраны с дисперсионной средой R1 = 4500 Ом, а сопротивление мембраны, заполненной 0,1 М раствором KCl, составляет R2 = 52 Ом. Удельная электропроводность 0,1 М раствора KCl равна χKCl = 1,167 См·м — 1 .
Задача 206. Рассчитайте толщину диффузного ионного слоя λ на поверхности частиц сульфата бария, находящихся в водном растворе NaCl концентрацией 25 мг/л. Относительная диэлектрическая проницаемость раствора при 288 К равна ε = 82,2.
Задача 207.Рассчитайте электрокинетический потенциал на границе керамический фильтр – водный раствор KCl, если при протекании раствора под давлением р = 3,1·10 4 Па потенциал течения составил U = 1,2·10 — 2 В. Свойства дисперсионной среды при 298 К: удельная электропроводность χ = 0,141 См·м — 1 (0,01 М раствор KCl), вязкость среды η = 8,94·10 — 4 Па·с, относительная диэлектрическая проницаемость ε = 78,5.
Задача 208. Поток света с длиной волны λ = 528 нм, проходя через эмульсию CCl4 в воде толщиной слоя l = 5 см, ослабляется в результате светорассеяния в два раза. Рассчитайте радиус частиц дисперсной фазы, если ее объмное содержание cV = 0,8 %, показатель преломления CCl4 n = 1,460, воды n0 = 1,333. Свет рассеивается в соответствии с уравнением Рэлея и ослабляется по закону Бугера-Ламберта-Бера.
Задача 209. Критическая концентрация мицеллообразования (ККМ) додецилсульфата натрия при 20, 40 и 60 о С составляет соответственно 1,51·10 — 3 ; 1,62·10 — 3 и 1,87·10 — 3 моль/л. Рассчитайте стандартную теплоту, энергию Гиббса и энтропию мицеллообразования при 20 о С.
Задача 210. Постройте кривую кинетики набухания каучука в четыреххлористом углероде в координатах α–τ по следующим экспериментальным данным:
| Время набухания τ, мин | ||||||||
| Степень набухания ατ | 0,33 | 1,15 | 2,33 | 2,91 | 3,25 | 3,41 | 3,58 | 3,58 |
Определите графическим способом константу скорости набухания К.
Задача 211. Постройте график зависимости приведенного осмотического давления от концентрации раствора сополимера стирола и метакриловой кислоты в толуоле (Т = 300 К) по следующим данным:
| Концентрация р-ра С·10 — 3 , г/м 3 | 1,1 | 2,8 | 5,4 | 7,6 |
| Осмотическое давление π, Па | 9,8 | 37,3 | 106,4 | 187,4 |
По графической зависимости π/С=f(C) определите относительную молекулярную массу М полимера и значение второго вириального коэффициента А2.
Задача 212. Экспериментально получена зависимость общего числа частиц гидрозоля золота в 1 м 3 υΣ от времени коагуляции τ, вызванной электролитом NaCl:
| τ, с | |||||
| υΣ·10 -14 , част/м 3 | 20,2 | 8,08 | 5,05 | 3,67 | 3,31 |
Вязкость среды η = 10 3 Па·с, температура 293 К.
Покажите применимость уравнения Смолуховского для описания кинетики коагуляции данного золя. Рассчитайте время половинной коагуляции θ и константу скорости быстрой коагуляции Кб. Сравните значение константы скорости быстрой коагуляции, рассчитанной теоретически, с экспериментальной величиной.
Задача 213. Рассчитайте и постройте потенциальную кривую взаимодействия сферических частиц диаметром 200 нм в водном растворе NaCl, если потенциал φσ = 20 мВ, константа Гамакера А* = 0,5·10 — 19 Дж, параметр χ = 1·10 8 м — 1 и температура 293 К. Значения суммарной энергии взаимодействия частиц определите при расстояниях между их поверхностями h = 2, 5, 10, 20 и 40 нм.
Задача 214. Реологические свойства 20%-ной суспензии бентонитовой глины в исследуемом интервале нагрузок описываются реологической моделью, состоящей из последовательно соединенных элемента Гука и модели Кельвина–Фойгта со следующими параметрами: модуль упругости элемента Гука Е = 1,5·10 3 Па; модуль эластичности Еэ=1,3·10 3 Па; вязкость элемента Ньютона η= 1,2·10 5 Па·с. Рассчитайте деформацию, развивающуюся в системе за 100 с при напряжении сдвига Р = 10 Па.
Задача 215. При изучении структурно-механических свойств графитовых паст глубина погружения конуса пластометра Ребиндера составляла h=2 мм при нагрузке F = 3 Н. Константа конуса KL = 0,4. Рассчитайте предельное напряжение сдвига графитовой пасты.
Задача 216. При изучении структурно-механических свойств суспензий пылевидного кварца с помощью прибора Вейлера–Ребиндера определено усилие Fмакс=1,5·10 — 2 Н, необходимое для смещения рабочей пластины прибора. Длина пластины 1 см, ширина 0,5 см. Рассчитайте предельное напряжение сдвига Pm суспензии.
Задача 217.При измерении вязкости растворов полистирола в толуоле с помощью капиллярного вискозиметра (типа вискозиметра Оствальда) получены следующие данные:
| Концентрация раствора С, г/л | 1,70 | 2,12 | 2,52 | 2,95 | 3,40 | |
| Время истечения раствора τ, с | 97,6 | 115,6 | 120,2 | 124,5 | 129,8 | 134,9 |
Рассчитайте значения относительной, удельной, приведенной вязкости растворов полимеров и постройте график зависимости ηуд/С = f(C). Определите характеристическую вязкость [η] и значение вискозиметрической константы Хаггинса К΄.
Задача 218. Рассчитайте толщину гидратных оболочек δ золя Al2O3, если реологическими измерениями установлено, что при концентрации 12 % (масс.) золь является ньютоновской жидкостью с вязкостью η = 1,18·10 — 3 Па·с. Радиус частиц золя r равен 10 нм. Плотность частиц дисперсной фазы ρ = 4 г/см 3 , дисперсионной среды ρ0 = 1 г/см 3 . Вязкость дисперсионной среды η0 = 1,18·10 — 3 Па·с. Коэффициент формы частиц α = 2,5.
Задача 219. Образец вулканизата массой 1,7564 кг, изготовленный на основе синтетического каучука СКН-26, поместили в бензол. Через 24 часа выдержки при 25 0 С масса этого образца стала равной 5,3921·10 -2 кг. Рассчитайте степень набухания этого вулканизата в бензоле при указанных условиях.
Задача 220. Характеристическая вязкость раствора образца синтетического каучука СКИ-3 в толуоле при 20 о С равна 4,62·10 — 3 м 3 /моль. Рассчитайте среднюю молярную массу этого каучука в условиях испытания. Постоянные k и α уравнения Штаудингера принять равными 5,14·10 — 5 моль/м 3 и 0,67.
Задача 221. По нижеприведенной зависимости осмотического давления, измеренного при 25 о С, от концентрации полистирола в бензоле рассчитайте среднюю молярную массу полимера при условиях опыта:
| ρi, кг/м 3 | 1,660 | 4,170 | 6,570 | 9,180 | 11,38 | 13,36 |
| πi, Па | 46,3 | 120,9 | 197,8 | 287,3 | 374,0 | 465,0 |
Задача 222. На коагуляцию гидрозоля иодида серебра из 1,0·10 — 2 м 3 сточных вод КБО потребовалось 8,0·10 — 4 м 3 10 %-го раствора NaCl (плотность 1,07·10 3 кг/м 3 ). Рассчитайте расход 28%-го раствора Al2(SO4)3 (плотность 1,30·10 3 кг/м 3 ) для извлечения AgI из 100 м 3 указанных сточных вод, если заряд коллоидных частиц иодида серебра в этих водах: а) положительный; б) отрицательный.
Задача 223. Белок плазмы крови человека (альбумин) имеет молекулярную массу 69000. Рассчитайте осмотическое давление раствора, содержащего 2 г этого белка в 100 мл, при 25 о С.
Задача 224. Суспензия 1 г гемоглобина в 1 л воды имеет осмотическое давление 3,6×10 — 4 атм при 25° С. Определите вес частицы гемоглобина.
Задача 225. При измерении осмотического давления раствора g-глобулина в 0,15 М NaCl при 37° С получены следующие данные:
| Концентрация g-глобулина С, г-на 100 мл | Осмотическое давление Р, мм Н2О |
| 19,27 | |
| 12,35 | |
| 5,81 |
Определите молекулярный вес g-глобулина.
Задача 226. Установлено, что связь между истинной вязкостью и молекулярным весом (М) раствора полиизобутилена при 20 о С описывается формулой h=3,60×10 — 4 М 0,64 . Определите молекулярный вес фракции полиизобутилена в растворе с истинной вязкостью 1,80 дл×г — 1 . Истинная вязкость может быть найдена из уравнения
[h] =
где h0 — вязкость растворителя, а C- концентрация, выраженная в граммах на 1 децилитр.
Задача 227. а) Какова поверхность куба, имеющего ребро 1 см? б) какова общая площадь поверхности того же материала,если он размельчен на кубики коллоидного размера, имеющие ребро 10 — 7 см. Выразите результат в м 2 .
Задача 228.Адсорбция азота на древесном угле исследовалась при -77° С, причем найдено, что 0,0946 г образца угля адсорбировали следующие количества азота х при указанном давлении Р.
| Р, атм | х, г | Р, атм | х, г |
| 3,5 | 0,0119 | 25,7 | 0,0192 |
| 10,0 | 0,0161 | 33,5 | 0,0195 |
| 16,7 | 0,0181 | 39,2 | 0,0196 |
| 48,6 | 0,0199 |
Нанесите на диаграмму эти данные таким образом, чтобы получить прямую линию в соответствии со следующими зависимостями, и оцените постоянные. Нет необходимости строить графики по уравнениям в их данной форме. Сначала, если необходимо, переведите уравнения в форму, которая дает прямолинейную зависимость; т — вес угля (г).
а) 

Задача 229. Получены следующие данные по адсорбции на древесном угле уксусной кислоты из водных растворов (во всех случаях объем раствора с углем был постоянным, 200 мл):
| Co, молярность уксусной кислоты в растворе до добавления угля | Се, молярность уксусной кислоты, оставшейся в растворе при равновесии | Вес угля m, г |
| 0,503 | 0,434 | 3,96 |
| 0,252 | 0,202 | 3,94 |
| 0,126 | 0,0899 | 4,00 |
| 0,0628 | 0,0347 | 4,12 |
| 0,0314 | 0,0113 | 4,04 |
| 0,0157 | 0,00333 | 4,00 |
Покажите, что эти данные удовлетворяют изотерме адсорбции Фрейндлиха
где х – количество граммов адсорбированной уксусной кислоты. Оцените постоянные k и n.
Задача 230. Во сколько раз дисперсность частиц сульфадимезина, молотого на струйной мельнице, больше дисперсности частиц сульфадимезина фармакопейного, если удельные поверхности их порошков соответственно равны 3600 и 210 м 2 /кг (форма частиц сферическая, плотность 1,80 г/см 3 )?
Задача 231. Важной физико-химической характеристикой порошка является его удельная поверхность. От нее зависит стабильность при хранении, прессуемость и скорость растворения порошка. Как отличаются удельные поверхности порошков пенталгина, выпускаемого тремя заводами, если дисперсности равны: 0,0458; 0,0472; 0,0564 мкм -1 (форма частиц сферическая, плотность 1,41 г/см)?
Задача 232. Для приготовления лекарственной мази на основе гепарина натрия необходимо определить дисперсность частиц гепарина натрия согласно следующим данным: время оседания частиц в водной среде на расстояние 0,2 м составляет 1,36×10 5 с, плотность гепарина натрия – 2,42 г/см 3 , плотность среды — 1,4 г/см 3 , вязкость среды – 1,8×10 -3 Пах (форма частиц сферическая).
Задача 233. Концентрация гидрозоля золота — 2 г/дм 3 , плотность золота 19,3 г/см 3 , частицы имеют сферическую форму с радиусом 510 — 9 м.Сколько частиц содержится в 1 м 3 золя? Какова удельная поверхность частиц (м — 1 )?
Задача 234. Определите удельную поверхность порошка сульфата бария (в расчете на единицу массы), если частицы BaSO4 оседают в .водной среде на 20 см за 20 мин. Плотность сульфата бария составляет 4,5; воды — 1 г/см 3 , вязкость воды — 1×10 — 3 Па×с (форма частиц сферическая).
Задача 235.Для приготовления лекарственной болтушки на основе оксида цинка необходимо определить дисперсность частиц ZnO по следующим данным: время оседания частиц в водной среде на расстояние 1 см составляет 30 с; плотность ZnO — 4 г/см 3 ;плотность среды — 1 г/см 3 ; вязкость среды — 1-10 — 3 Па×с(форма частиц сферическая).
Задача 236. Вычислите удельную поверхность частиц бентонита (форма частиц сферическая), если время их оседания на расстояние 2 см составляет 100 с. Плотность дисперсной фазы – 2,7 г/см 3 ; дисперсионной среды – 1,1 г/см 3 , вязкость дисперсионной среды – 2,5×10 -3 Па×с
Задача 237. Концентрация гидрозоля серебра — 1 г/дм , плотность серебра -10,5 г/см , частицы имеют форму куба с длиной ребра 5,0 нм. Сколько частиц содержится в 1 дм золя? Какова удельная поверхность частиц (м — 1 )? Каково осмотическое давление золя при 293 К?
Задача 238. Напишите формулу мицеллы гидрозоля, полученного конденсационным методом с помощью химической реакции с указанным стабилизатором (табл. 1) и определите ионы, образующие потенциалопределяющий, адсорбционный и диффузный слои:
| № п/п | Химическая реакция | Стабилизатор |
| 238.1 | CaCl2 + (NH4)2C2O4 → CaC2O4 + 2NH4Cl | CaCl2 |
| 238.2 | CaCl2 + (NH4)2C2O4 → CaC2O4 + 2NH4Cl | (NH4)2C2O4 |
| 238.3 | 2CuSO4 + K4[Fe(CN)6] → Cu2[Fe(CN)6] + 2K2SO4 | CuSO4 |
| 238.4 | 2CuSO4 + K4[Fe(CN)6] → Cu2[Fe(CN)6] + 2K2SO4 | K4[Fe(CN)6] |
| 238.5 | Na2S + CuSO4 → CuS + Na2SO4 | Na2S |
| 238.6 | Na2S + CuSO4 → CuS + Na2SO4 | CuSO4 |
| № п/п | Химическая реакция | Стабилизатор |
| 238.7 | 2KI + Pb(NO3)2 → PbI2 + 2KNO3 | KI |
| 238.8 | 2KI + Pb(NO3)2 → PbI2 + 2KNO3 | Pb(NO3)2 |
| 238.9 | Fe2(SO4)3 + 2K3PO4 → 2FePO4 + 3K2SO4 | Fe2(SO4)3 |
| 238.10 | Fe2(SO4)3 + 2K3PO4 → 2FePO4 + 3K2SO4 | K3PO4 |
| 238.11 | Na2SiO3 + 2HCl → H2SiO3 + 2NaCl | Na2SiO3 |
| 238.12 | Na2SiO3 + 2HCl → H2SiO3 + 2NaCl | HCl |
| 238.13 | Ni(NO3)2 + K2S → NiS + 2KNO3 | Ni(NO3)2 |
| 238.14 | Ni(NO3)2 + K2S → NiS + 2KNO3 | K2S |
| 238.15 | CoCl2 + 2NaOH → Co(OH)2 + 2NaCl | CoCl2 |
| 238.16 | CoCl2 + 2NaOH → Co(OH)2 + 2NaCl | NaOH |
| 238.17 | Pb(CH3COO)2 + H2SO4 → PbSO4 + 2CH3COOH | Pb(CH3COO)2 |
| 238.18 | Pb(CH3COO)2 + H2SO4 → PbSO4 + 2CH3COOH | H2SO4 |
| 238.19 | ZnSO4 + Na2CO3 → ZnCO3 + Na2SO4 | ZnSO4 |
| 238.20 | ZnSO4 + Na2CO3 → ZnCO3 + Na2SO4 | Na2CO3 |
| 238.21 | 2KMnO4 + 3KNO2 + H2O → 2MnO2 + 3KNO3 + 3KOH | KMnO4 |
| 238.22 | AlCl3 + 3NaOH → Al(OH)3 + 3NaCl | AlCl3 |
| 238.23 | AlCl3 + 3NaOH → Al(OH)3 + 3NaCl | NaOH |
| 238.24 | Na2SO3 + CaCl2 → CaSO3 + 2NaCl | Na2SO3 |
| 238.25 | Na2SO3 + CaCl2 → CaSO3 + 2NaCl | CaCl2 |
| 238.26 | Ba(OH)2 + Pb(NO3)2 → Pb(OH)2 + Ba(NO3)2 | Ba(OH)2 |
| 238.27 | Ba(OH)2 + Pb(NO3)2 → Pb(OH)2 + Ba(NO3)2 | Pb(NO3)2 |
| 238.28 | 2Na3PO4 + 3CaCl2 → Ca3(PO4)2 + 6NaCl | Na3PO4 |
| 238.29 | 2Na3PO4 + 3CaCl2 → Ca3(PO4)2 + 6NaCl | CaCl2 |
| 238.30 | Cu(NO3)2 + 2KOH → Cu(OH)2 + 2KNO3 | Cu(NO3)2 |
| 238.31 | Cu(NO3)2 + 2KOH → Cu(OH)2 + 2KNO3 | KOH |
| 238.32 | CuSO4 + H2S → CuS + H2SO4 | CuSO4 |
| 238.33 | CuSO4 + H2S → CuS + H2SO4 | H2S |
| 238.34 | MgCl2 + Na2HPO4 + NH4OH → MgNH4PO4 + 2NaCl | MgCl2 |
| 238.35 | BaCl2 + K2CrO4 → BaCrO4 + 2KCl | BaCl2 |
| 238.36 | BaCl2 + K2CrO4 → BaCrO4 + 2KCl | K2CrO4 |
| 238.37 | AsH3 + AgNO3 + H2O → Ag + HNO3 + H3AsO3 | AgNO3 |
| 238.38 | K2Cr2O7 + 2AgNO3 → Ag2Cr2O7 + 2KNO3 | K2Cr2O7 |
| 238.39 | K2Cr2O7 + 2AgNO3 → Ag2Cr2O7 + 2KNO3 | AgNO3 |
| 238.40 | 2H3AsO3 + 3H2S → As2S3 + 6H2O | H2S |
| 238.41 | H2S + ½ O2 → S + H2O | H2S |
| 238.42 | 8KMnO4 + 3Na2S2O3 + H2O → →8MnO2 + 3Na2SO4 ++ 3K2SO4 + 2KOH | KMnO4 |
| 238.43 | Ba(NO3)2 + K2SO4 → BaSO4 + 2KNO3 | Ba(NO3)2 |
| 238.44 | Ba(NO3)2 + K2SO4 → BaSO4 + 2KNO3 | K2SO4 |
| 238.45 | 3K4[Fe(CN)6] + 4FeCl3 → Fe4[Fe(CN)6] + 12KCl | K4[Fe(CN)6] |
| 238.46 | 3K4[Fe(CN)6] + 4FeCl3 → Fe4[Fe(CN)6] + 12KCl | FeCl3 |
| 238.47 | AgNO3 + KBr → AgBr + KNO3 | AgNO3 |
| 238.48 | AgNO3 + KBr → AgBr + KNO3 | KBr |
| 238.49 | KAuO2 + 3HCHO + K2CO3 → 2Au + 3HCOOK ++ KHCO3 + H2O | KAuO2 |
| 238.50 | FeCl3 + 3H2O → Fe(OH)3 + 3HCl | FeOCl |
Задача 239. Какова дисперсность частиц амиксина, если удельная поверхность порошка амексина 140 м /кг, а плотность – 1,55 г/см 3 (форма частиц сферическая)?
🌟 Видео
Поверхностные явленияСкачать

Поверхностное натяжение (видео 3) | Силы межмолекулярного взаимодействия | ХимияСкачать
Адсорбция на твёрдой поверхностиСкачать

Адсорбция (Киевнаучфильм)Скачать
Уравнение ЛенгмюраСкачать

АдсорбцияСкачать

8.1 Поверхностно-активные вещества | Химия вокруг насСкачать

Адсорбция. Простой эксперимент дома / ХимХопСкачать

Поверхностные явления. Адсорбция.Скачать

Поверхностно-активные веществаСкачать

Коллоидная химия. Лекция 1. Физико-химия поверхностных явленийСкачать

Адсорбция на границе фаз раствор-воздух (лабораторная работа)Скачать

Растворение. Растворимость веществ в воде | Химия 8 класс #39 | ИнфоурокСкачать

Поверхностные явленияСкачать

Коллоидные растворы ПАВ (мицеллярные растворы, лиофильнные растворы) | Коллоидная химия | Лекция 5Скачать

Адсорбция на силикагелеСкачать

АдсорберыСкачать