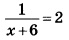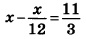9 задание 9 333007 решите уравнение (7 видео)

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Содержание

Калькулятор онлайн. Решение показательных уравнений.
Немного теории.
Показательная функция, её свойства и график
Показательные уравнения
Задание №9 ОГЭ по математике
Теория к заданию №9
Задание 9 ЕГЭ по математике. Графики функций
🎦 Видео

Видео:ОГЭ 2024. Математика. Задание 9. УравненияСкачать

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Видео:ОГЭ для НОЛИКОВ, Уравнения N-9Скачать

Немного теории.

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, ( a neq 1)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, ( a neq 1), не имеет корней, если ( b leqslant 0), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Видео:ВСЕ ТИПЫ 9 ЗАДАНИЯ ОГЭ 2023 МАТЕМАТИКАСкачать

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, ( a neq 1), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac = 1 ), откуда ( left( frac right) ^x = 1 ), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
( left( frac right) ^ = 1 )
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Видео:9)Решите уравнение 7х+9=4х. ОГЭ математика 2023. Канал Математика бесплатно. ОГЭ по математике.Скачать

Задание №9 ОГЭ по математике

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.

Найдите корень уравнения:

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x – 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

Затем делим обе части на 10:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

Так как в ответе просят указать наименьший корень, то это -4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

Далее вычисляем дискриминант:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

pазбирался: Даниил Романович | обсудить разбор | оценить

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

режде всего, исключим

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выполним умножение в левой части уравнения и раскроем скобки справа:

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

Переносим 12 из левой части в правую:

ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите корень уравнения:

Обе части уравнения приводим к единому знаменателю 12: 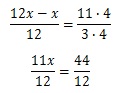Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем: 11х=44 х=44:11 х=4

pазбирался: Даниил Романович | обсудить разбор | оценить

Имеем линейное уравнение:

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ОГЭ N338480 Решите уравнение.Скачать

Задание 9 ЕГЭ по математике. Графики функций

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №9 ЕГЭ.

Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 9 в формате ЕГЭ-2021

Линейная функция

1. На рисунке изображён график функции . Найдите значение , при котором

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

Вычтем из первого уравнения второе:

Уравнение прямой имеет вид:

Найдем, при каком значение функции равно -13,5.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции

Вычтем из первого уравнения второе.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен

Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой

Для точки пересечения прямых:

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть

5. На рисунке изображен график функции . Найдите с.

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид .

6. На рисунке изображён график функции Найдите

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

Формула функции имеет вид:

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому

График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

Найдем абсциссу точки B. Для точек A и B:

(это абсцисса точки A) или (это абсцисса точки B).

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

График функции проходит через точку (2; 1); значит,

График функции проходит через точки (2; 1) и (1; -4), — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда

Для точек A и B имеем:

Отсюда (абсцисса точки A) или (абсцисса точки B).

9. На рисунке изображён график функции . Найдите f (6,76).

Функция задана формулой:

Ее график проходит через точку (4; 5); значит,

10. На рисунке изображен график функции . Найдите .

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда =5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:

Поделим второе уравнение на первое:

Подставим во второе уравнение:

12. На рисунке изображен график функции . Найдите

График функции проходит через точку Это значит, что

формула функции имеет вид: .

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

Вычтем из второго уравнения первое:

или — не подходит, так как (как основание логарифма).

14. На рисунке изображен график функции .

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на .

16. На рисунке изображён график функции

На рисунке — график функции Так как

График функции проходит через точку A Подставим и координаты точки А в формулу функции.

Так как получим:

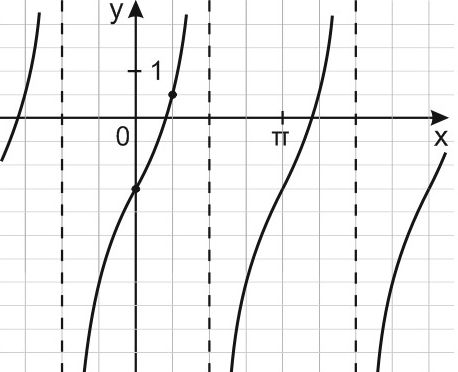
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 9 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.