9 коагуляция быстрая и медленная кинетика быстрой коагуляции уравнение м смолуховского

План лекции:

Видео:Быстрая речь Как замедлить речьСкачать

АГРЕГАТИВНАЯ УСТОЙЧИВОСТЬ

Под агрегативной устойчивостью подразумевают сохранение межфазовой поверхности и поверхностной энергии.

Агрегативная устойчивость определяется способностью дисперсных систем противодействовать слипанию частиц. Взаимодействие и слипание твердых частиц приводит к образованию агрегатов. В результате происходит укрупнение частиц, структура дисперсной фазы изменяется, а агрегаты приобретают способность оседать или всплывать. Агрегация и укрупнение частиц называется коагуляцией.

Все дисперсные системы по механизму образования классифицируются:

1. Лиофильные — получаются при самопроизвольном диспергировании одной из фаз.

2. Лиофобные — получаются в результате диспергировании с конденсацией с пересыщением (не самопроизвольно)

В лиофобных системах, если они не закреплены стабилизатором, идут самопроизвольные процессы укрупнения частиц. Такие системы называют агрегативно-неустойчивыми.

Укрупнение может идти двумя путями:

1. изотермическая перегонка — перенос вещества от мелких частиц к крупным,

2. коагуляция — слипание частиц.

Агрегативная устойчивость нестабилизированных систем носит кинетический характер и судить о ней можно по скорости процессов, вызываемых избытком поверхностной энергии. Агрегативная устойчивость может носить и термодинамический характер, если дисперсная система не обладает избытком поверхностной энергии.

Видео:Вьетнамская Техника Оздоровит Сердце и Мозг. Как расслабить сосуды мозга и сердца - 1Скачать

ТЕРМОДИНАМИЧЕСКИЕ И КИНЕТИЧЕСКИЕ ФАКТОРЫ УСТОЙЧИВОСТИ ДИСПЕРСНЫХ СИСТЕМ

1. Электростатический — уменьшение межфазного натяжения из-за возникновения ДЭС на поверхности частиц.

2 .Адсорбционно-сольватный — уменьшение межфазного натяжения при взаимодействии частиц дисперсной фазы со средой.

3. Энтропийный — действует в системах, где частицы участвуют в тепловом движении.

4. Структурно-механический — на поверхности частиц имеются пленки, обладающие упругостью и механической прочностью, разрушение их требует затраты энергии.

5. Гидродинамический — уменьшение скорости коагуляции, благодаря изменению вязкости среды.

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

ИЗОТЕРМИЧЕСКАЯ ПЕРЕГОНКА

Изотермическая перегонка может происходить практически во всех системах. Частицы разных размеров обладают неодинаковыми химическими потенциалами, что создает движущую силу переноса вещества от мелких частиц к крупным. Этот процесс ведет к исчезновению мелких частиц, уменьшению средней дисперсности, уменьшению свободной энергии поверхности.

1.растворение и испарение мелких частиц,

2.перенос вещества к крупным частицам,

3.рост крупных частиц.

(1) и (3) стадии — химические процессы, (2) стадия диффузионная.

Скорость изотермической перегонки часто лимитируется (2) стадией, которая подчиняется закону Фика и зависит от градиента концентраций или давлений, которые, в свою очередь, определяются размером частиц

(9.1)

где D с — скорость диффузионного массопереноса (разность концентраций у поверхности малой и большой частиц, V _М — мольный объем, r _ср — средний радиус частиц, s — поверхностное натяжение.

То есть перенос вещества зависит от:

3.растворимости дисперсной фазы,

Если дисперсная фаза хорошо растворима в дисперсионной среде, то система обладает малой устойчивостью по отношению к изотермической перегонке. Этим объясняется невозможность получения высокодисперсных систем при хорошей растворимости дисперсной фазы. Межфазное натяжение способствует переносу вещества.

Видео:Как быстро убрать слизь в горле? | Чудо-упражнение от мокротыСкачать

КИНЕТИКА КОАГУЛЯЦИИ

Коагуляция протекает в термодинамически неустойчивых дисперсных системах. Смолуховским была рассмотрена коагуляция монодисперсных золей со сферическими частицами, которые сталкиваются между собой в результате броуновского движения.

Чтобы определить число столкновений, рассматривают диффузный поток частиц через сферу, окружающую одну частицу, фиксированную в начале координат. Коэффициент диффузии движущейся частицы равен сумме коэффициентов диффузии сталкивающихся n — и m -мерных частиц.

Поток через сферическую частицу по закону Фика:

концентрация частиц : n _{n m} = k _{n m} n _m n _n (9.4),

Умножим (9.2) на (9.3), получим:

(9.6)

При каждом столкновении два агрегата дают один.

d n / d t = k n _t 2 , решение этого выражения дает уравнение Смолуховского:

(9.7)

t _к — время коагуляции, n ₀ — исходная концентрация системы.

Различают кинетику медленной и быстрой коагуляции.

Быстрая коагуляция.

При быстрой коагуляции все столкновения частиц эффективны, то есть приводят к слипанию частиц. Быстрой коагуляции отвечает условие равенства нулю потенциального барьера D Е = 0 и равенство единице стерического множителя Р = 1.(Р учитывает благоприятные пространственные расположения частиц при столкновении).

Константа скорости быстрой коагуляции равна :

Если учесть, что R = 2 r , D = k _БТ/(6 p h r ),то

Из соотношения (9.9) следует, что константа скорости быстрой коагуляции зависит только от температуры и вязкости среды. Вязкость жидкостей, как правило, уменьшается с повышением температуры, что обуславливает резкую зависимость константы скорости коагуляции от температуры.

Медленная коагуляция.

D Е не равна нулю.

Связь эффективности соударений с потенциальным барьером была показана Фуксом. Он ввел понятие коэффициента замедления W , который показывает, во сколько раз К_м меньше К_б.

Видео:Как механически очищать почки? Упражнения при опущении почек и мочекаменной болезниСкачать

ТЕРМОДИНАМИЧЕСКАЯ ТЕОРИЯ АГРЕГАТИВНОЙ УСТОЙЧИВОСТИ ДИСПЕРСНЫХ СИСТЕМ

Лиофильные (термодинамически агрегативно устойчивые) дисперсные системы могут образовываться самопроизвольно. То есть из любого агрегатного состояния система переходит в данное состояние с уменьшением D G , то есть лиофильные системы — равновесные и обратимые.

D G = D Н — Т D S 0

D Н характеризует межфазное натяжение, D Н не может уменьшаться до 0, так как система должна оставаться гетерогенной.

Наличие D S возможно у дисперсных систем, частицы которых способны к броуновскому движению. То есть из свободнодисперсных систем термодинамически устойчивыми могут быть только ультрамикрогетерогенные — золи.

Условие термодинамической агрегативной устойчивости.

( ¶ D G / d S ) _s 0 и ( ¶ D G / d r ) _s 0 (9.12)

Это означает, что D G не должно увеличиваться с ростом межфазной поверхности или с уменьшением размера частиц.

Наиболее типичные представители лиофильных коллоидных систем — растворы коллоидных поверхностно активных веществ (ПАВ) и высокомолекулярных соединений (ВМС).

Термодинамически устойчивые к коагуляции лиофобные системы могут быть рассмотрены аналогично лиофильным, если представить уже раздробленную и стабилизированную фазу.

Стабилизаторы увеличивают энтропийную составляющую. Такие системы не могут образовываться самопроизвольно, но могут самопроизвольно пептизировать после коагуляции.

Энергия Гиббса смешения D G _N — мера термодинамической агрегативной устойчивости дисперсных систем.

(9.13)

SHAPE * MERGEFORMAT

n = n _{+ +} n _— — стехиометрический коэффициент диссоциирующей частицы.

Условие т/д агрегативной устойчивости: D G _N 0,

Критическое значение межфазного натяжения, выше которого система теряет агрегативную устойчивость ( D G _N = 0).

(9.14)

При отсутствии ДЭС ( n = 1)

(9.15)

d — средний размер частиц, n — безразмерный множитель, учитывающий влияние концентрации и формы частиц.

Чтобы использовать это уравнение для более конкретного рассмотрения влияния различных факторов на агрегативную устойчивость ионно-стабилизированных систем, оно было преобразовано: Стехиометрический коэффициент можно представить с помощью числа способных к диссоциации поверхностных функциональных групп А₀ на единице поверхности, степени их диссоциации a и заряда противоионов z :

(9.16)

Подставим в это выражение (9.14), получим:

(9.17)

Из общих критериальных соображений следует, что критическое межфазное натяжение тем выше, чем больше стехиометрический коэффициент диссоциирующей частицы и меньше размер частиц и их концентрация. Диссоциация частиц лиофильных систем облегчает образование системы. Для стабилизации лиофобных систем необходимо обеспечить достаточную плотность способных к диссоциации групп на поверхности частиц, их диссоциацию, а также образование ДЭС.

Таким образом, т/д устойчивость к коагуляции лиофобных систем может быть обеспечена путем формирования поверхностных слоев, способных уменьшить межфазное натяжение и увеличить энтропию до требуемых значений.

Видео:Лучшие приёмы для сердца омолодят сосуды за 1 минуту в день!Скачать

Кинетика коагуляции. Медленная и быстрая коагуляция

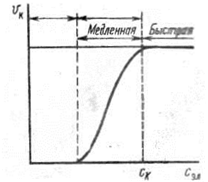
Ход коагуляции в зависимости от концентрации коагулирующего электролита можно подразделить на две стадии (рис. 12): медленную и быструю. При медленной коагуляции изменение концентрации коагулирующего электролита сопровождается резким изменением скорости коагуляции. В области быстрой коагуляции увеличение концентрации коагулирующего электролита не вызывает изменение скорости коагуляции, достигшей своего максимального значения. Концентрацию электролита, начиная с которой скорость коагуляции остается постоянной, называют порогом быстрой коагуляции.

Рис 12 Зависимость скорости коагуляции от концентрации электролита.

Теория быстрой коагуляции была разработана М.Смолуховским. Она основана на предположении, что в области быстрой коагуляции любое столкновение частиц приводит к их слипанию и что все мицеллы золя до коагуляции имеют одинаковый размер и сферическую форму. Число столкновений в единицу времени определяется интенсивностью броуновского движения частиц. Для количественного описания коагуляции М.Смолуховский использовал уравнения формальной химической кинетики. При этом были использованы следующие допущения:

1) при столкновении двух первичных частиц, из которых состоял золь до начала коагуляции, появляются более крупные частицы, называемые вторичными;

2) при столкновении вторичных частиц с первичными появляются третичные частицы;

3) частицы более высокого, четвертого, порядка образуются либо в результате слипания двух вторичных частиц, либо третичной частицы с первичной; подобные процессы приводят к образованию частиц большей кратности.

При увеличении концентрации электролита начинается образование частиц низших (I, II, III и т.п.) порядков, которое протекает незаметно для невооруженного взгляда и называется поэтому скрытой коагуляцией. Дальнейшее увеличение концентрации электролита ведет к прогрессивному развитию коагуляции, повышению её скорости и сопровождается появлением частиц более высоких порядков. Золь претерпевает видимые изменения: он мутнее или изменяется его окраска. Эта стадия процесса называется явной коагуляцией.Переход скрытой в явную называется порогомкоагуляции.

Уравнение скорости быстрой коагуляции можно представить как реакцию второго порядка:

(13)

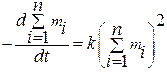
где к – константа скорости, m=∑m_i=m₁+m₂+m₃+…+m_i – общая концентрация частиц всех порядков (кратности) в системе, m₁, m₂, m₃, …, m_i – соответственно концентрации первичных, вторичных, третичных, I – ой кратности частиц.

М. Смолуховский развил теорию медленной коагуляции частиц, сохраняющих некоторую стабильность, предполагая, что не каждое столкновение частиц приводит к их слипанию. Кинетика медленной коагуляции развита в работах Н.А.Фукса. Если эффективной является лишь часть столкновений α, то константа скорости реакции равна:

(14)

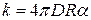
При коагуляции вместе с уменьшением числа частиц и их укрупнением происходит изменение ряда свойств растворов: понижается скорость диффузии и фильтрации частиц, увеличивается скорость седиментации, меняется интенсивность рассеянного света, а вместе с тем и окраска растворов.

Вопрос 7. Коллоидная защита, физический смысл явления

Коагуляция в ряде случаев зависит от способа прибавления электролита-коагулятора. Экспериментальные данные свидетельствуют о том, что если электролит добавлять к золю небольшими порциями, то в итоге коагуляция наступает при более высокой концентрации электролита, чем при внесении сразу большого его количества. Такое явление называется привыканием золя.Причиной привыкания золя может быть образование пептизатора или адсорбция ионов, заряженных одноименно с частицей, что приводит к повышению первоначального заряда частицы. Устойчивость лиофобных золей против коагуляции возрастает в присутствии ВМВ: белков, полисахаридов и т.п. Это проявляется в повышении значений порогов коагуляции у защищенного золя и неподчинению правилу Шульце-Гарди.

Механизм защитного действия можно объяснить тем, что макромолекулы ВМВ адсорбируются на поверхности коллоидных частиц, создавая адсорбционные сольватные слои, которые повышают гидрофильность коллоидных частиц. Вследствие этого усиливается взаимодействие частица-растворитель. Сольватные слои обеспечивают большее расклинивающее давление при сближении двух частиц и препятствуют их слипанию. Защитное действие усиливается, если в адсорбционном слое ВМВ образуются гелеобразные структуры, обладающие повышенной прочностью и упругостью (это относится, например к желатину).

В то же время при малых добавках ВМВ в ряде случаев наблюдается не повышение, а снижение устойчивости коллоидов. Это явление называют сенсибилизацией.Объяснить механизм сенсибилизации можно тем, что при малой концентрации ВМВ на частицах образуется рыхлый адсорбционный слой, часть поверхности частиц остается свободной и возрастает вероятность адсорбции одной макромолекулы различными участками на двух частицах дисперсной фазы. Происходит коагуляция путем «сшивания» частиц.

Р.Зигмонди предложил количественное определение защитного действия того или иного защитного коллоида – так называемое золотое число. Известно, коллоидное золото, весьма чувствительное к прибавкам электролита, в высокодисперсном состоянии имеет красный цвет. При уменьшении степени дисперсности золь золота приобретает голубой цвет.

Золотое число выражается количеством миллиграммов защитного коллоида, которое достаточно, чтобы предотвратить изменение цвета 10 мл красного золя золота в голубой при прибавлении 1 мл 10%-ого раствора хлорида натрия.

Чем меньше золотое число, тем больше защитное действие коллоида. Различные защитные коллоиды обладают отличающимся действием и, следовательно, характеризуются различным золотым числом.

Было определено также защитное действие в отношении золей серебра (серебряное число), конго рубинового (рубиновое число), серы и т.д.

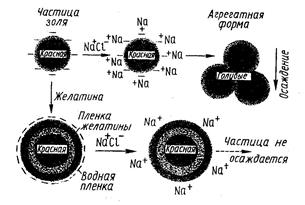
На рис. 13 схематично изображен процесс осаждения золя золота под действием электролита и защитное коллоидное действие желатина на золь. Частица золя золота в результате адсорбции анионов приобретает заряд. В отсутствие защитного коллоида эта частица не обладает защитной оболочкой из молекул растворителя и поэтому при добавлении в раствор хлорида натрия легко осаждается. Ионы натрия нейтрализуют заряд золя, частицы золя уже не отталкивают друг друга и агрегируют.

Рис 13 Защитное действие желатина на золь золота.

Если к золю добавить желатин, белок прикрепляется к частицам золя и образует вокруг них защитную пленку. Ионная поверхность желатина сообщает частицам дополнительный заряд, как положительный, так и отрицательный. Поверхность белка адсорбирует молекулы воды, что обеспечивает частицам золя золота добавочную защиту. Добавление хлорида натрия уменьшает заряд золя, но не столь эффективно, как это наблюдалось в отсутствии защитного коллоида. В результате частица не осаждается.

Вопрос 8. Приложение понятия коагуляции к биосистемам

Процессы коагуляции и пептизации имеют большое значение для жизнедеятельности организмов, так как коллоиды клеток и биологических жидкостей также подвержены коагуляции и постоянно испытывают воздействие со стороны электролитов. Согласно правилу Шульце-Гарди для сохранения постоянства физико-химических условий в организме и при экспериментах in vitro необходимо соблюдать постоянство не только концентрации электролитов, но и их качественного состава. Действительно, если приготовить изотонический раствор не из NaCL, а из равной концентрации многозарядных ионов, хотя бы Mg(OH)₂, то двухзарядные ионы будут обладать значительно более сильным коагулирующим действием на коллоиды, чем NaCL.

Значение коллоидной защиты для биологии и фармации чрезвычайно велико. Принцип коллоидной защиты используют при получении колларгола, золей серебра, золота и т.д. Частицы колларгола так хорошо защищены, что не коагулируют даже при высушивании. Белки крови защищают капельки жира, холестерин и другие гидрофобные вещества от коагуляции. Ослабление защитных функций белков крови приводит к отложению холестерина на стенках сосудов, образованию камней в почках, печени и т.п

Дата добавления: 2016-11-04 ; просмотров: 9355 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Доктор Куте: вот как мы в Японии за 5 минут разгоняем кровь по всему телуСкачать

Лако-красочные материалы — производство

Видео:Запоминай БЫСТРО и ЛЕГКО - 6 простых способовСкачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Каошики (каушики) танец со спины. Медленный темп. Танцуем вместеСкачать

КИНЕТИКА КОАГУЛЯЦИИ

Прежде чем перейти к обсуждению причин устойчивости и коа­гуляции лиозолей, рассмотрим теорию кинетики коагуляции, кото­рая, кстати говоря, была разработана гораздо раньше теории устойчивости коллоидных систем.

Различают быструю и медленную коагуляцию. Под быстрой коагуляцией подразумевают такую коагуляцию, при которой все сближения частиц, находящихся в броуновском движении, кон­чаются их слипанием. При медленной коагуляции вследствие того, что на поверхности коллоидных частиц частично сохранился двой­ной электрический слой^сольвауная оболочка и т. д., слипание ча — стйцПп^»йсхбдатг»лишь» в результате особо удачных сближений. Таким образом, оба термина являются вполне условными.

Теория кинетики быстрой коагуляции создана польским уче­ным Смолуховским. Основные положения, из которых исходил Смолуховский, сводятся к тому, что между частицами золя дей­ствуют силы притяжения и отталкивания; последние ослабевают при введении электролита и при концентрации электролита, вы­зывающей быструю коагуляцию, исчезают вовсе. Дальнейшее при­бавление электролита не может ускорить коагуляцию. Частицы такого астабилизованного золя при сближении в процессе броу­новского движения на достаточно близкое расстояние слипаются под давлением сил молекулярного притяжения, образуя агрегат, который совершает в дальнейшем броуновское движение как одно целое. Природу сил, действующих между частицами, Смолухов­ский не рассматривал.

Для экспериментального изучения кинетики коагуляции необхо­димо было определить изменение концентрации частиц в золе по мере коагуляции. Это можно было бы осуществить путем счета частиц с помощью ультрамикроскопа. Однако определение числен­ной концентрации таким методом весьма длительно, а коагуляция протекает обычно очень быстро, так что к концу счета концентра­ция частиц в золе оказалась бы совсем иной, чем в его начале. Выход был найден в том, что в золь, в который был уже введен электролит и который таким образом находился в состоянии коа­гуляции, в определенный момент вводился стабилизатор, «обры­вающий» коагуляцию. В таком стабилизованном золе численная
концентрация частиц уже не меняется и его можно исследовать с помощью ультрамикроскопа. В качестве стабилизатора для «об­рыва» коагуляции обычно применялся желатин. В настоящее вре­мя метод, основанный на счете частиц в неподвижном объеме, не — применяется.

Кювременный метод изучения процесса коагуляции основан на счете частиц в потоке. Поточный ультрамикроскоп, разработанный впервые Б. В. Дерягиным и Г. Я. Власенко, описан в гл. II. Этим прибором можно определять численную концентрацию, не преры­вая процесса коагуляции, во много раз быстрее, чем по старому способу. Одновременно новый способ устраняет многие источник»

Ошибок, присущие старому методу изме­рения численной концентрации золя. Не­давно этот метод был усовершенствовав Мак Файденом и А. Смитом.

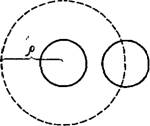
Смолуховский при создании своей теории принимал, что скорость быстро» коагуляции, т. е. изменение численной концентрации частиц в единицу времени, зависит от численной концентрации зо­ля v, от интенсивности броуновского движения, характеризующейся коэффи­циентом броуновской диффузии частиц D, и от критического расстояния р, на которое должны приблизиться друг к другу центры двух частиц, чтобы произошло слипание частиц. Расстояние р может превышать диаметр коллоидных частиц, (рис. IX, 1). Таким образом, если представить се, бе сферу радиу­са р, центр которой совпадает с центром одной из частиц, друга» частица прилипнет к ней только тогда, когда центр второй части­цы коснется поверхности этой сферы, называемой сферой погло­щения. При расстояниях, больших р, действием молекулярных сил притяжения на броуновское движение частиц и на процесс их. сближения Смолуховский полностью пренебрегал.

Рис. IX, 1. Схема, поясняю­щая сферу действия частиц при быстрой коагуляции.

При быстрой коагуляции агрегация, согласно Смолуховскому, идет таким образом, что первоначальные одинарные частицы, стал­киваясь друг с другом, образуют двойные частицы, затем двойные частицы, сталкиваясь с одинарными, образуют тройные и т. Д — Возможны столкновения между собой и сложных частиц. Одно­временное столкновение трех н более простых или сложных частиц возможно, но вследствие малой вероятности такого события Смо­луховский для упрощения теории не принимал в расчет подобные столкновения.

Обозначая через vi, V2r V3 … численные концентрации частиц, состоящих из одной, двух, трех и т. д. первоначальных частиц, можно написать, что в начале, когда время т = О

V, = v0 и va = v3 = … v„ = О

По истечении времени т

V = vt = Vj + v2 + v3 + … где v — конечная численная концентрация.

При этом, очевидно, будет соблюдаться неравенство:

Но Д, = 0 и Ді = 0, так как все направления смещений равновероятны. По­этому Д, Ді = 0 и, следовательно

Таким образом, средние квадраты смещений всех частиц относительно первой удваиваются. Благодаря связи Д2 с коэффициентом диффузии можно сказать, что броуновское движение остальных частиц относительно первой характери­зуется вдвое большим коэффициентом диффузии D‘. В результате этого время от времени частицы будут сближаться с первой до критического расстояния их Центров р. Подсчитаем число таких сближений, не учитывая тех осложнений, которые возникают при изменении броуновского движения вследствие слипания частиц. Для этого примем, что после сближения частиц до расстояния центров р соответствующая частица как бы поглощается центральной. Пусть частицы за­ключены в очень большой объем. Допустим также, что в рассматриваемый мо­мент коагуляции численная концентрация v равна vT. Однако в непосредствен­ной близости от поверхности поглощающей сферы концентрация частиц близка к нулю, так как ввиду беспорядочного характера броуновского блуждания ве­роятность попадания частицы, находившейся вблизи поглощающей сферы, в эту сферу очень велика, а вероятность избежать этого мала. При удалении от сферы р быстро достигаются значения vT. Совокупное перемещение частиц, со­вершающих независимо друг от друга беспорядочные блуждания, описывается уравнением диффузии. Допустим, что концентрация частиц v(R) зависит только От расстояния R от начала координат, к которому направлен поток диффузии, вызванный поглощением частиц сферой радиуса р. В этом случае из законо» диффузии следует:

Где Q — число частиц, проходящих за единицу времени через поверхность сфе­ры s радиуса R по направлению к центральной частице.

Число Q, очевидно, равно числу частиц, поглощенных за единицу времена центральной частицей при сближении с ней, т. е. Q равно искомой частоте актов агрегации с участием центральной частицы.

Учитывая граничное условие

Которое следует из того, что частицы, достигнув сферы р, поглощаются централь­ной частицей, и интегрируя уравнение (IX, 5), получим:

Учитывая другое граничное условие

Общее число сближений всевозможных частиц в единице объема можно опреде­лить, умножая Q на численную концентрацию v и деля полученное произведе­ние на 2, так как иначе каждая пара частиц будет подсчитана дважды. Заменяя D‘ на 2D, получим:

Сравнивая это уравнение с уравнением (IX, 1), мы найдем значение константы к в уравнении Смолуховского (IX, 2):

Следует заметить, что формула Смолуховского предполагает существование на­чального момента коагуляции, до которого слипания частиц не происходило. Поэтому в начальный момент центральная частица окружена частицами, кон­центрация которых всюду равняется Vo. Вследствие этого в начале процесса Коагуляции частота сближения и слипаний несравненно больше, чем величина Q В уравнении (IX, 9). Однако очень скоро именно благодаря высокой начальной частоте сближений концентрация частиц вблизи центральной уменьшается до нуля, и за доли секунды установится распределение частиц, подчиняющееся уравнению (IX, 6). После этого скорость коагуляции будет подчиняться уравне­нию Смолуховского.

Однако через некоторое время начнутся отклонения от закона Смолухов­ского, Основная причина заключается в том, что коэффициент к в формуле (IX, 2), выведенный при рассмотрении процесса сближения двух одинарных ча­стиц, принимает иное значение при сближении с агрегатом слипшихся частиц другого агрегата или даже одиночной частицы.

Придав уравнению (IX, 1) вид:

И проинтегрировав его в пределах от vo до v и от 0 до т, получим:

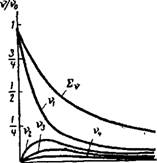
Рнс. IX, 2. Зависимость от­носительного числа частиц различного порядка от т/0 при быстрой коагуляции.

Откуда численная концентрация золя в момент т будет равна:

Вводя время половинной коагуляции 9, можем написать

Тогда основное уравнение (IX, 12) можно представить так:

По уравнению IX, 14, зная vo и v для различных значений т, можно вычислить 0 и к.

Графически зависимость относитель­ных изменений общего числа частиц £ v и числа частиц vi, V2, V3 … в единице объема золя от т/0 показана на рис. IX, 2. Из уравнения (IX, 14) следует, что 1/v есть линейная функция времени т. Это следствие теории неоднократно было подтверждено на опыте.

Теория Смолуховского позволяет так­же вычислить расстояния р, на которые должны приблизиться центры двух ча­стиц для того, чтобы произошло их сли­пание.

Kv0 4itЈ>pv0 И, согласно Эйнштейну,

Где K — константа Больцмаиа; т) — динамическая вязкость дисперсионной среды; Г — радиус частиц,

То, комбинируя два последних уравнения, получим:

Согласно эксперименту, р/г = 2,3, следовательно, расстояние р довольно близко к 2г, т. е. силы аттракции начинают действовать

Лишь тогда, когда частицы приблизятся на весьма малые расстоя­ния, на которых энергия ‘молекулярного притяжения становится намного больше энергии теплового, а следовательно, и броуновско­го движения 3likT.

Представления Смолуховского объясняют коагуляцию монодис­персных золей. Мюллер разработал подобную же теорию для объяснения коагуляции полидисперсных систем. Он показал, что частицы различных размеров агрегируются всегда скорее, чем оди­наковые частицы. При этом большие частицы играют роль как бы «зародышей» коагуляции; такую же роль могут играть и агрега­ты, образующиеся в начальной стадии коагуляций приблизительно монодисперсного золя золота, как об этом свидетельствуют на­блюдения Б. В. Дерягина и Н. М. Кудрявцевой. Впрочем, положе­ния Мюллера полностью верны лишь тогда, когда в золе имеются частицы, существенно превосходящие по размеру малые частицы. Теория Мюллера объясняет автокаталитический характер коагу­ляции, скорость которой может постепенно возрастать со временем. Мюллер также показал, что коагуляция ускоряется, если частицы имеют удлиненную форму, так как на поступательное броуновское движение налагается еще вращательное движение, увеличиваю­щее вероятность столкновения таких частиц.

Теория СМолуХовского, как мы неоднократно подчеркивали,, пригодна «Для быстрой коагуляции. Им было сделано предполо­жение, что разработанная «теория может быть приложима и к мед­ленной коагуляции, когда частицы не полностью астабилизованьи В этом случае в уравнение IX, 12, описывающее процесс коагуля­ции, следует ввести эффективность сближения є:

Однако, как следует из теории коагуляции Н. А. Фукса, приложи — мой к частицам, силы взаимодействия между которыми изменяют­ся с расстоянием по любому закону, параметру є надо придать другой смысл, так как понятие эффективности сближения по Смо — луховскому неприменимо к процессу сближения частиц, совер­шающих броуновское движение.

Теория Смолуховского предполагает, что до сближения частиц на опреде­ленное расстояние р никаких сил взаимодействия между ними нет. Для учета сил дальнодействия частиц, как функции от расстояния их центров R, Н. А. Фукс дополнил формулу (IX, 5) членом, выражающим дрейф частиц по направлению к центральной частице под влиянием сил притяжения F:

Где Р — подвижность частицы в вязкой среде, равная отношению ее скорости к действующей силе; цифра 2 перед р введена потому, что в действительности обе частицы движутся навстречу друг другу.

Согласно Эйнштейну р = D/kT, следовательно, 2|3 = D‘/kT. Далее, заме­няя силу F на dU/dR (где U — потенциальная энергия молекулярного взаимо­действия двух частиц) и интегрируя уравнение (IX, 18), вместо (IX,9) получим:

При £/(/?)= О снова получается формула (IX, 9). Уравнение (IX, 19) было выведено Н. А. Фуксом первоначально для аэрозолей с целью учета ускорения коагуляции под влиянием притяжения разноименно заряженных частиц. В этом случае потенциальная энергия взаимодействия отрицательна и скорость коагуля­ции возрастает.

В общем случае из (IX, 19) вместо (IX, 10) можно получить уравнение

И вместо константы Смолуховского к величину, меньшую в W раз, где

Величину W называют коэффициентом замедления. Легко видеть, что уравнение медленной коагуляции получится путем замены е на 1 /W. Таким образом, теория Фукса дает теоретическое истолкование коэффициента Смолуховского е.

Для коллоидной химии особый интерес представляет случай, когда между частицами преобладают силы отталкивания. При этом U(R)> 0, и если для каких-то значений R величина U<R) Много больше, kT, то значение Q становится крайне малым. Это Значит, Что скорость коагуляции настолько снизится, что можно говорить о практической агрегативной устойчивости системы.

Для исследования кинетики коагуляции Б. В. Дерягиным и Н. М. Кудрявце­вой был применен поточный ультрамикроскоп (по схеме, близкой к поточному ультрамикроскопу для аэрозолей Б. В. Дерягина и Г. Я. Власенко). С помощью поточного ультрамикроскопа можно определять за 2—3 мин численную концен­трацию гидрозолей вплоть до 1010—10″ частиц в 1 см3; другие способы счета частиц не позволяют измерять концентрацию больше 10*— 105 частиц в 1 см3. При применении достаточно концентрированных золей с помощью поточного микроскопа можно наблюдать не только быструю, но и медленную коагуляцию, отвечающую малым значениям коэффициента е, не затрачивая для этого чрез­мерно много времени.

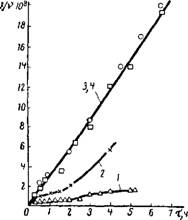
На рис. IX, 3 приведены графики зависимости І/v от времени т, прошедшего от начала коагуляционного процесса для сравнительно низкодисперсного голу­бого гидрозоля золота; отдельные кривые отвечают различным концентрациям коагулирующего электролита. Можно видеть, что при высокой концентрации электролита (кривые 3 и 4), при которой потенциальный барьер * исчезает, кине­тика коагуляции характеризуется линейной зависимостью, вытекающей из теории

Смолуховского. Несколько меньший наклон прямой к оси абсцисс объясняется согласно В. М. Муллеру тем, что на близких расстояниях вязкое сопротивление жидкой прослойки сближению сферических частиц возрастает по сравневию с сопротивлением, рассчитанным по формуле Стокса При малых концентрациях электролита линейная зависимость ^кривые 1, 2) нарушается. Типичной является кривая 2. После начального подъема кривой следует участок, почти параллель­ный оси абсцисс, и в некоторый момент происходит новый подъем кривой, в дальнейшем не прекращающийся. Согласно Б. В. Дерягину и Н. М. Кудрявцевой первоначальный подъем кривой и, следовательно, уменьшение численной концен­трации золя означает образование агрега­тов из двойных частиц. При малых концен­трациях электролита ближняя потенциаль­ная яма сравнительно не глубока, энерге­тические взаимодействия не велики и потому распады образовавшихся двойных частиц происходят с достаточной частотой.

Прн достижении определенной концен­трации двойных частиц их распады урав­новешивает процесс слипания одиночных частиц, вследствие чего численная концен­трация золя становится постоянной. В не­который момент к одной из двойных частиц прилипает третья частица, образуя тройную частицу. Энергия связи каждой из трех частиц образовавшегося агрегата в два раза больше, чем у частицы, входящей в двой­ную частицу. Поэтому такая тройная части­ца имеет мало шансов распасться. Одновре­менно происходит дальнейший рост агрега­тов за счет присоединения новых частиц. И действительно, визуальные наблюдения под микроскопом показали, что в некоторый момент среди сравнительно слабо видимых частиц (по «вспышкам» в поле зрения по­точного ультрамикроскопа) появляются все более яркие и коагуляция все более уско­ряется. Этнм объясняется форма кривых с перегибом. При более высоких концен­трациях электролита вследствие снижения энергетического барьера и углубления по­тенциальной ямы горизонтальные участки графика укорачиваются и, наконец, исчезают, ио S-образная форма кривых сохраняетсяГТаким образов, при изуче­нии коагуляции необходимо учитывать не только процессы агрегации, но и рас­пада агрегатов.

Дальнейшее развитие этих положений принадлежит Г. А. Мартынову и В. М. Муллеру. В определенных условиях может устанавливаться агрегативное равновесие между одинарными и агрегированными частицами. Хотя вероятность распада крупных агрегатов меньше, чем парных, все же уменьшение числа оди­нарных частиц в конечной стадии коагуляции может настолько понизить ско­рость образования новых агрегатов, что коагуляция будет уравновешена ско­ростью распада агрегатов. Следовательно, возможно равновесие между коагу­лятом и оставшимся разбавленным золем. Это явление, однако, не носит общего характера, так как существуют золи, коагулирующие необратимо, и обнаружен­ное поведение золей золота в работе Н. М Кудрявцевой, по-видимому, связано с частичной гидрофилизацией поверхности его частиц за счет адсорбции органи­ческих компонентов, остающихся в золе после его приготовления.

Рис. IX, 3. Кинетика коагуляции голубого гидрозоля золота в при­сутствии хлорида кални. Концентрация коагулирующего электро­лита (в моль/л): 1—5-Ю-3; 2—1 • Ю-2; 3 —5 • Ю-2; 4 — 1 • Ю-1.

Следует отметить, что учет образования и распада агрегатов и его ускоре­ния в градиентном потоке, как было показано уже давно Гудивом, Жнллепси и др., позволяет объяснить реологическое поведение тиксотропных суспензий, о чем будет сказано в гл. X.

От распада агрегатов в процессе коагуляции следует отличать явление пеп­тизации — распада агрегатов в результате изменения ионного состава диспер­сионной среды, о чем уже говорилось в гл. VIII. В этом случае пептизация происходит благодаря усилению электрической слагающей расклинивающего давления и уменьшению глубины потенциальной ямы.

🌟 Видео

Уникальная система умножения на 9!!!Скачать

Оптимизация дыхания. Быстрая коррекция 2Скачать

Соотношение быстрых и медленных мышечных волокон (Предрасположенность к Спорту, Генетика)Скачать

Строение, локализация и общие свойства быстрых и медленных мышечных волокон. 10 класс.Скачать

Операционный метод для задачи КошиСкачать

Кинематика. Из координаты получаем скорость и ускорениеСкачать

Закон Сложения Скоростей - Относительная скорость / Урок Физики 10 класс / КинематикаСкачать

УСТАЛИ ОТ ОТЕКОВ? Узнайте, как быстро ИЗБАВИТЬСЯ ОТ ОТЕКОВ и улучшить кровоток в организме!Скачать

Основы кинематики. Тема 7. Неравномерное движение. Средняя и мгновенная скоростьСкачать

Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать