Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Уравнения по условию задачи::
Решение системы уравнений:
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
$$ <left< begin P = 2(a+b) = 48 \ a = 3b end right.> Rightarrow <left< begin a+b = 24 \ a = 3b end right.> Rightarrow <left< begin 3b+b = 24 \ a = 3b end right.> Rightarrow <left< begin 4b = 24 \ a = 3b end right.> Rightarrow <left< begin a = 18 \ b = 6 end right.> $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
$$ <left< begin 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end right.> (-) Rightarrow <left< begin 7x+10y = 10050 \ x-y=185 | times 10 end right.>$$
$$ Rightarrow (+) <left< begin 7x+10y = 10050 \ 10x-10y = 1850 end right.> Rightarrow <left< begin 17x = 11900 \ y = x-185 end right.> Rightarrow <left< begin x = 700 \ y = 515 end right.> $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
$$ <left< begin 2x+3y = 1540 \ 2y-x = 210 | times 2 end right.> Rightarrow (+) <left< begin 2x+3y = 1540 \ -2x+4y = 420 end right.> Rightarrow <left< begin 7y = 1960 \ x = 2y-210 end right.> Rightarrow <left< begin x = 350 \ y = 280 end right.> $$
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
$$ Rightarrow <left< begin 5v-u = 73 \ v+7u = 29 end right.> Rightarrow <left< begin 5(29-7u)-u = 73 \ v = 29-7u end right.> Rightarrow <left< begin 145-35u-u = 73 \ v = 29-7u end right.> Rightarrow$$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
$$ <left< begin 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end right.> Rightarrow <left< begin 5x+3y = 170 |times frac \ 2,4x+6,5y = 284 end right.> Rightarrow (-) <left< begin 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end right.> $$
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ <left< begin x+ frac y = 44 | times 2 \ frac x+y = 44 end right.> Rightarrow (-) <left< begin 2x+y = 88 \ frac x+y = 44 end right.> Rightarrow (+) <left< begin 1frac x = 44 \ y = 88-2x end right.> Rightarrow $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
Из второго уравнения $ frac = frac = 0,25 $. Подставляем в первое уравнение:
И тогда искомое время:
$$ t = frac = 2cdot1,25 = 2,5 (ч) $$
Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Тренажеры по алгебре на тему «Задачи на составление систем уравнений» (7 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Тренажер Задачи на составление с/у.
1.Сумма двух чисел равна 131, а их разность -41. Найдите эти числа.
2. У Ивана 25 монет по 25 копеек и по 10 копеек, всего на сумму 1 руб. 50 коп.(1руб=100коп). Сколько 5-копеечных и сколько 10-копеечных монет у Ивана?
3. Брат и сестра, работая летом на почте, заработали 230 руб.Брат заработал на 40 руб больше сестры. Сколько заработал каждый?
4. Николай на выполнение домашней работы по математике затратил на 30 мин больше, чем по географии. Всего на эти два предмета у него ушло 1ч.40мин. Сколько времени потребовалось на каждый предмет?
5. Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них?
6. У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и сколько трехместных лодок было у причала?
7. На одно платье и 3 сарафана пошло 9м ткани, а на 3 таких же платья и 5 таких же сарафанов -19м ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
8. Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы – 35 кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?
9. Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 3 часа. Расстояние между поселками 30 км. Найдите скорость каждого пешехода, если у одного она на 2 км/ч меньше, чем у другого.
10.В городской думе заседало 60 депутатов, представляющие две партии. После выборов число депутатов от первой партии увеличилось на 12%, а от второй партии – уменьшилось на 20%. Сколько депутатов от каждой партии оказалось в городской думе после выборов, если всего было выбрано 56 депутатов?
11, Школьная баскетбольная команда в двух играх заработала 95 очков. Если удвоить количество очков, полученных в первой игре, то это на 5 меньше, чем количество очков, полученных во второй игре. Сколько очков заработала каждая команда в каждой игре?
12. Мотоциклист ехал 3 ч. По проселочной дороге и 0,5ч. По шоссе, всего он проехал 110км. Скорость мотоциклиста по шоссе была на 10 км/ч больше, чем по проселочной дороге. С какой скоростью ехал мотоциклист по шоссе, а с какой – по проселочной дороге?
13. В зале расставили одинаковыми рядами 48 стульев. Рядов оказалось на 8 больше, чем стульев в каждом ряду. Сколько стульев в каждом ряду и сколько рядов в зале?
14. Все имеющиеся яблоки можно разложить в 6 пакетов или в 4 коробки. Сколько кг яблок имеется, если в пакет помещается на 1 кг яблок меньше, чем в коробку?
15. Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 5ч, а второй за 4ч, так как изготовлял в час на 12 деталей больше первого. Сколько деталей изготовил каждый рабочий?
16. Во время путешествия Николай проделал путь в 1100 км на самолете и на автобусе. На автобусе он пролетел расстояние в 4,5 раза большее, чем проехал на автобусе. Какое расстояние Николай пролетел на самолете?
Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Урок алгебры «Решение задач с помощью систем уравнений» (7-й класс)
Разделы: Математика
Класс: 7
Цели:
- научить детей решать задачи с помощью составления систем уравнений;
- познакомить и литературным наследием родного края, вспоминая творчество П.П.Бажова;
- использовать при решении задач факты окружающей действительности.
1. Подготовка к восприятию материала (проверка опорных знаний)
Учитель, используя медиапроектор, восстанавливает изученную ранее тему. Детям задаются вопросы их предполагаемые ответы, воспроизводятся на экране.
Вопросы:
- Посмотрите на экран, что вы видите? (Презентация. Слайд 1)
- Что такое система уравнений? (Презентация. Слайд 2)
- Какие способы решения систем уравнений вы знаете? (Презентация. Слайд 3)
- Давайте вспомним суть применения каждого способа (Презентация. Слайды 4, 5, 6).
– Система уравнений не только позволяет установить общие корни уравнений, содержащихся в ней, но и становится хорошим помощником при решении задач. В таких задачах неизвестных компонентов более одного и они связаны друг с другом условием. Сегодня мы рассмотрим задачи, в которых неизвестно два каких либо элемента и будем учиться решать такие задачи с помощью составления системы уравнений.
Дети записывают в тетрадях число, тему урока. (Презентация. Слайд 7)
2. Изучение новой темы
Задача 1
– Рассмотрим для примера такую задачу.
Я знаю, что в классе 20 учеников. Среди них есть девочки и мальчики. А еще я знаю, что девочек больше чем мальчиков на 4 человека. Сколько мальчиков и девочек в этом классе? Ответ можно узнать двумя способами: 1) просто пересчитать; 2) решить такую задачу: (Презентация. Слайд 8)
Пусть х – количество девочек
y – количество мальчиков
Т.к. мальчиков и девочек вместе – 20. Получим уравнение: х + у = 20
С другой стороны девочек больше чем мальчиков на 4
Значит можно получить следующее уравнение х – у = 4
Объединим оба эти уравнения в систему, т.к в каждом уравнении речь идет об одних и те же детях., получим: 
Далее дети самостоятельно решают систему уравнений, на листочках под копирку.
Ответ: В классе 8 мальчиков и 12 девочек.
3. Самостоятельная работа в парах
У вас на партах лежат цветные карточки. На экране появятся условия задач. Вы выбираете для решения ту задачу, которая расположена на таком же цветном фоне, что и цвет вашей карточки. (Слайд 9)
Записывают составленную систему на тех же листочках под копирку.
Задача 2
1) В Зоопарке г. Екатеринбурга, живет много разных животных. Среди них есть медведи – бурые и белые. Известно, что всего в зоопарке живет 9 медведей, а бурых на 5 медведей больше, чем белых. Сколько белых и бурых медведей живет в зоопарке г. Екатеринбурга?
Решение:
Ответ: В зоопарке 2 белых медведя и 7 бурых медведей.
2) В Зоопарке г. Екатеринбурга, живет много разных животных. Среди них есть лисы – черные и рыжие. Известно, что всего в зоопарке живет 7 лис, а черных на 3 лисы меньше, чем рыжих. Сколько черных и рыжих лис живет в зоопарке г. Екатеринбурга?
Решение
Ответ: В зоопарке 5 рыжих лисиц и 2 черные лисицы.
После того как дети самостоятельно составили систему уравнений – листочки сдают, проверка. Решать эти системы они будут дома.
– Вы должны поднять карточку в том случае, если система составлена правильно. (Презентация. Слайд 10)
4. Закрепление материала
– А сейчас, я хочу рассказать вам об очень интересном человеке. Он родился в 28 января 1879 году, в семье мастера Сысертского завода. И отец, и дед его, и прадед всю жизнь провели на медеплавильных заводах Сысертского горного округа. В 1899 году он стал народным учителем и трудовой свой путь начал в глухой уральской деревне Шайдурихе, возле старинного города Невьянска.
С детства он прислушивался к рассказам рабочих об их тяжелой жизни, позже изучил много документов, рассказывающих о горнозаводском Урале. В летние каникулы он пешком или на велосипеде путешествовал по уральским заводам и деревням, по реке Чусовой, изучал труд камнерезов и гранильщиков, сталеваров и литейщиков, беседовал с ними о тайнах их ремесла
Люди говорили, что живет в горах Малахитница (Хозяйка Медной горы), охраняет камни, рядом с ней всегда много ящериц, а иногда и сама ящерицей оборачивается.
А звали этого интересного человека Павел Петрович Бажов. (Презентация. Слайд 11)
Колдун уральский бородатый,
Бажов дарит нам новый сказ.
«Живинка в деле» – сказ богатый
И поучительный для нас.
В нем слово каждое лучится,
Его направленность мудра,
Найдут, чему здесь поучиться,
Любого дела мастера
Важны в работе ум и чувство,
В труде двойное естество
«Живинкой в деле» мастерство
Преображается искусство,
И нет тогда ему границ.
И совершенству нет предела,
Не оторвать тогда от дела
Ни мастеров, ни мастериц.
Их вдохновение безмерно,
Глаза их пламенем горят.
Они работают? Неверно.
Они – творят.
– Вы знаете его сказы или повести?
– Что означает слово «сказ»?
Сказ – это литературное произведение, в котором рассказчиком является не сам писатель, а другой, вымышленный им человек.
– В сказах Бажова живет хранительница недр, покровительница уральских рудокопов. Как ее зовут?
– Хозяйка Медной горы. (Презентация. Слайд 12)
– В каких сказах Бажова встречается Хозяйка Медной горы?
- Малахитовая шкатулка,
- Каменный цветок
- Горный мастер
- Хрупкая веточка
- Таюткино зеркальце
- Две ящерки
- Приказчиковы подошвы
- Сочневы камешки
– В сказах Бажова главными героями выступали и дети (Презентация. Слайд 13), это такие сказы как:
- Тяжелая витушка
- Серебряное копытце
- Хрупкая веточка
- Каменный цветок
- Огневушка-Поскакушка
- Таюткино зеркальце
- Малахитовая шкатулка
- Жабреев ходок
- Голубая змейка
– У меня в руках книга, в которой собраны произведения П.П.Бажова. Она называется «Малахитовая шкатулка». В этой книге разное количество сказов и повестей. Книга большая и в ней много страниц.
Я знаю, что 2 сказа о Хозяйке Медной горы и 3 сказа о героях-детях занимают 94 страницы. А 3 сказа о Хозяйке Медной горы и и 4 сказа о героях детях занимают 133 страниц. Помогите мне узнать, сколько страниц может занимать 1 сказ о Хозяйке Медной горы и 1 сказ о героях-детях?
Х стр. – о Х. М.г. 2х + 3у = 94
У стр. – о Д. 3х + 4у = 133
Получим систему
Ответ: 1 сказ о ХМг занимает 23 страницы; 1 сказ о детях занимает 16 страниц
Старик Кокованя приютил у себя сироту. Девочка Даренка была смышленая и чудная. Встретилась она с волшебным козлом, которого прозвали Серебряное копытце. При каждой встрече с ним можно было собрать много каменьев. При первой встрече Даренка собрала два мешочка гранатов и три мешочка малахита, всего 1300 гр. А при второй встрече один мешочек гранатов и два мешочка малахит, всего 800 грамм. Сколько грамм самоцветов содержится в каждом мешочке с малахитом и в каждом мешочке с гранатом?
Хгр – 1 мешочек малахита 2у + 3х = 1300
Угр – 1 мешочек граната у + 2х = 800
Получим систему
Ответ: В 1 мешочке 300гр малахита и 200гр. граната
– Я предлагаю каждому из вас, вернувшись, домой, прочитать сказы Бажова, ведь он писал их для нас.
5. Подведение итогов урока, выставление оценок.
– Итак, подведем итоги. Какая сегодня у нас была тема урока?
– Что нового вы узнали, чему научились?
– Остались ли у вас вопросы, на которые учитель должен будет ответить на следующем уроке?
6. Домашнее задание
- Решить задачу 1 графическим способом.
- Составить и решить задачу, в которой вы можете узнать возраст своих родителей, с помощью системы уравнений.
💡 Видео
АЛГЕБРА 7 класс. Решение задач с помощью систем уравненийСкачать

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Решение задач с помощью систем уравнений, 7 классСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

Решение задач с помощью уравнений. Алгебра, 7 классСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение задач с помощью систем уравнений | Алгебра 7 класс #48 | ИнфоурокСкачать

Алгебра 7 класс (Урок№49 - Решение задач при помощи систем уравнений первой степени.)Скачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Решение задач с помощью уравнений. Алгебра 7 классСкачать

7 класс, 5 урок, Задачи на составление линейных уравнений с одной переменнойСкачать

Система уравнений. Метод алгебраического сложенияСкачать

№ 10.1. Задачи на составление систем уравнений (7 класс)Скачать
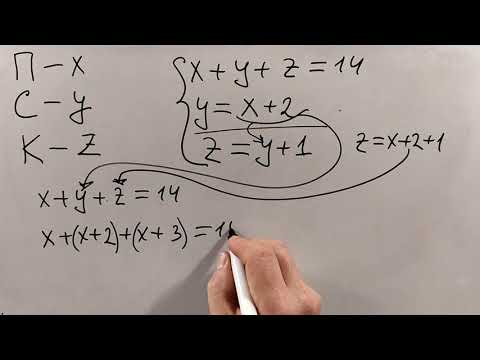
Алгебра 7 класс Составление и решение задач с помощью систем уравненийСкачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

7 класс// АЛГЕБРА // Решение задач с помощью систем уравненийСкачать




