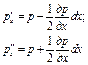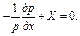Рассмотрим некоторый объем покоящейся жидкости (рис. 1.4). Выделим в ней вокруг рассматриваемой точки А бесконечно малый параллелепипед с ребрами dx, dy, dz. Отбросим мысленно окружающую его жидкость, а ее воздействие на грани заменим силами, действующими со стороны жидкости, — Рх и Р’х, Ру и F, Рг и Р Кроме того, в точке А как в центре массы выделенного элемента приложим равнодействующую массовых сил Q.
Рис. 1.4. Схема к выводу уравнения Эйлера
Запишем условие равновесия на осьх:
Давление рх и р’х можно выразить через давления в точке А:
Тогда уравнение равновесия перепишется
Отсюда +рХ = 0, или — = рХ.
Аналогичные уравнения можно получить, рассматривая проекцию на другие оси.
В результате будем иметь
Это и есть общие уравнения равновесия жидкости, полученные Эйлером.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
ВЫВОД ФОРМУЛЫ ПРИРАЩЕНИЯ ДАВЛЕНИЯ И ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПОВЕРХНОСТИ РАВНЫХ ДАВЛЕНИЙ
Основной задачей гидростатики является получение:
• зависимости гидростатического давления в точке от ее координат
• уравнения поверхности равных давлений
Для получения уравнения изменения давления при смещении от данной точки А на бесконечно малое расстояние dl, проекции которого на оси координат соответственно будут dx, dy, dz, преобразуем уравнения Эйлера. Умножим соответственно каждое уравнение на приращения координатах, dy, dzn, суммировав левые и правые части, получим
Но левая часть этого уравнения есть полный дифференциал dp, выражающий изменение давления р при смещении точки на бесконечно малое расстояние, тогда имеем
То есть получили дифференциальное уравнение изменения давления в функции координат точки. Решение этого уравнения в виде (1.13) может быть выполнено путем интегрирования для данной конкретной задачи.
Перейдем к рассмотрению уравнения поверхности равного давления, определяемого условием р = const.
Из условия постоянства давления следует dp = 0. Подставляя это выражение в (1.15) и учитывая, что р ф 0, получим
Уравнение (1.16) связывает координаты точек равных давлений, т.е. оно является дифференциальным уравнением поверхности равных давлений.
Решение этого уравнения в виде (1.14) должно также проводиться путем интегрирования для конкретных задач. К рассмотрению одной из таких задач и перейдем.
Видео:Определяем тип ДУ 1Скачать
Дифференциальные уравнения равновесия жидкости
Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед с ребрами dx, dy, dz, параллельными осям координат х, у, z (рис. 3.6). Выберем в центре параллелепипеда точку А. Давление в этой точке будет р = f(х, у, z). Так как это давление является непрерывной функцией координат, то, разлагая функцию f(х, у, z) в ряд Тэйлора в окрестности точки А с точностью до бесконечно малых первого порядка, получим следующие соотношения для давлений р1 и р2 в точках 1 и 2 на гранях параллелепипеда, перпендикулярных оси х:
Давления на гранях параллелепипеда можно также записать в виде отношения силы к площади:
(3.9)
Запишем условие равновесия сил, действующих на элементарный параллелепипед, в проекции на ось х:
(3.10)
где Fm – массовая сила, определяемая по формуле
(3.11)
где dm – масса элементарного параллелепипеда.
Рис. 3.6. Схема сил, действующих на элементарный параллелепипед
Подставляя формулы (3.9), (3.11) в соотношение (3.10), получаем
Подставляя формулы для р1 и р2, найдем
Аналогичные уравнения можно получить, если спроецировать действующие на параллелепипед силы на оси у и z. В итоге будем иметь систему трех дифференциальных уравнений вида
(3.12)
где X, Y, Z – проекции ускорений массовых сил, приходящихся на единицу массы.
Эти уравнения впервые были выведены Эйлером в 1755 г. и называются уравнениями равновесия Эйлера. Они показывают, что при равновесии жидкости массовые силы уравновешиваются соответствующими поверхностными силами.
В векторной форме эти уравнения имеют вид
где 
; 
(i, j, k – орты координатных осей, имеющие координаты (1; 0; 0), (0; 1; 0), (0; 0; 1) соответственно).
Видео:Закон БернуллиСкачать
Потенциал массовых сил
Умножая уравнения Эйлера (3.12) соответственно на dx, dy, dz и почленно складывая, получаем
(3.13)
Так как р = f (x, y, z), полный дифференциал этой функции будет
Следовательно, правая часть уравнения (3.13) есть полный дифференциал:
(3.14)
Равенство (3.14) имеет смысл лишь в том случае, если левая его часть есть также полный дифференциал какой-то функции. Обозначим эту функцию через и = и(х, у, z). Тогда полный дифференциал ее будет
(3.15)
Из сопоставления уравнений (3.14), (3.15) получим
Функцию и = и(х, у, z) называют потенциальной функцией, а силы, для которых эта функция существует, – силами, имеющими потенциал.
Отсюда вывод: жидкость может находиться в равновесии только под действием массовых сил, имеющих потенциал, так как только такие силы удовлетворяют уравнениям равновесия Эйлера.
Видео:6. Особые решения ДУ первого порядкаСкачать
Интеграл уравнений Эйлера для несжимаемой жидкости
Проинтегрируем уравнение (3.15) при р = const:
(3.16)
где с – постоянная интегрирования. Полагая, что при р = р0 потенциальная функция и = u0, будем иметь
(3.17)
Подставляя выражение (3.17) в соотношение (3.16), получаем
Последнее соотношение является интегралом уравнений Эйлера для несжимаемой капельной жидкости.
Так как величина ρ(u-u0) не зависит от давления р0 и определяется лишь системой массовых (но не поверхностных) сил, следовательно, на сколько изменится давление p0, на столько же изменится и давление р в любой точке жидкости. Отсюда можно сформулировать закон Паскаля: давление в жидкости, находящейся в равновесии, передается всем ее частицам без изменения сто величины.
Введем понятие поверхности равного давления и выведем ее уравнение.
Поверхностью равного давления называется такая выделенная в жидкости поверхность, гидростатическое давление во всех точках которой одно и то же. Для такой поверхности, очевидно, dp = 0. Так как р = f(x, у, z), уравнение поверхности равного давления р = const будет
Придавая С различные значения, будем переходить от одной поверхности равного давления к другой. Это уравнение является уравнением семейства поверхностей равного давления. Поверхности равного давления и равного потенциала совпадают. Так как —ρdu = dp, при dp = 0 du = 0 и и = const.
Определение поверхности равного давления по заданным массовым силам производится по уравнению
(3.18)
Ввиду отсутствия массовых сил по осям х, у и с учетом того, что массовая сила по оси z Z = -g, уравнение (3.18) примет вид —ρgdz = 0, или dz = 0. Отсюда z = const.
Следовательно, поверхности равного давления, в том числе и свободная поверхность, – горизонтальные плоскости.
Видео:Дифференциальные уравнения. 11 класс.Скачать
Дифференциальные уравнения равновесия жидкости
(уравнения Эйлера)
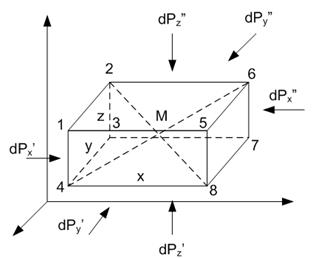
Выделим в покоящейся жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными осям координат и равными соответственно dx, dy, dz (рис. 2.4, стр. 61).
Со стороны окружающей жидкости на выделенный параллелепипед действуют поверхностные силы, определяемые гидростатическим давлением, а также массовые силы, пропорциональные его массе.
Составим уравнение равновесия для этой системы сил в проекциях на координатную ось Ох. При этом будем предполагать, что гидростатическое давление есть непрерывная функция координат пространства и что его значение в центре тяжести параллелепипеда (точка М) равно р. Тогда первое уравнение равновесия в проекциях на ось Ох запишется следующим образом:
(2.2)
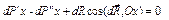
где dP ’ x=P ’ xdydz – сила гидростатического давления на грань 1-2-3-4; dP ” x =P ” x — то же, на грань 5-6-7-8;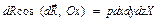 
— проекция элементарной массовой силы на ось Ох;P’x, и P”— среднее гидростатическое давление соответственно на грани 1-2-3-4 и 5-6-7-8.
Рис. 2.4. Расчетная схема для составления уравнений равновесия жидкости
Так как гидростатическое давление является функцией координат, значения давлений P’x и P ” x будут:
Тогда уравнение (1.1) примет вид:
(2.3)
(2.3)
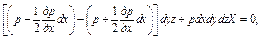
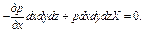
Разделив уравнение (1.16) на массу параллелепипеда, получим:
Проделав аналогичные операции с проекциями внешних сил на оси Оy и Оz, получим систему дифференциальных уравнений равновесия жидкости:
(2.4)
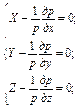
Эта система уравнений была впервые получена в 1755 г. Эйлером.
Умножим каждое уравнение (2.4) соответственно на dx, dy и dz и сложим их:
(2.5)
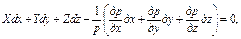
Давление является функцией только трех независимых переменных координат х, у и z, поэтому левая частьуравнения (2.5) представляет собой полный дифференциал функции р=f(х, у, г).
Уравнение (2.6) называется основным дифференциальным уравнением равновесия жидкости. Отметим, что при выводе этого уравнения мы не вводили никаких дополнительных ограничений на массовые силы и на плотность жидкости р, поэтому оно имеет общий характер к может быть использовано и для сжимаемой жидкости.
Левая часть уравнения (2.6) представляет собой полный дифференциал, следовательно, и правая его часть также должна быть полным дифференциалом. Если же принять плотность жидкости или газа постоянной или независимой от х, у и z, то выражение в скобках также будет полным дифференциалом некоторой функции U = f(x,y,z),частные производные которой, взятые по х, у, z,равны проекциям ускорений массовых сил на соответствующие оси:
(2.7)
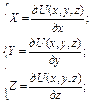
Величины X, У и Z можно рассматривать как проекции массовых сил, отнесенных к единице массы данной жидкости поэтому функцию U=f( х, у,z) называют потенциальной или силовой функцией, а силы, удовлетворяющие условию (2.7), — силами, имеющими потенциал. Таким образом, при рассмотрении уравнения (2.6) с учетом выражения (2.7) можно сделать важный вывод: равновесие жидкости возможно только в том случае, когда массовые силы имеют потенциал.
Заметим далее, что в основном уравнении равновесия жидкости неизвестны только две величины ρ и р (значения же проекций единичных массовых сил X, Y и Z, а также координаты точки предполагаются заданными). Следовательно, для получения однозначного решения уравнения (2.7) нужно воспользоваться так называемым характеристическим уравнением, которое определяло бы связь между физическими свойствами и состоянием рассматриваемой жидкости, например связь между плотностью жидкости, ее температурой и давлением.
Поверхность, в каждой точке которой значение данной функции постоянно, называется поверхностью уровня. Физический смысл функции и ее значения могут быть различными (например, поверхность равной температуры, равного давления и т. п.). В механике жидкости наибольший интерес представляет поверхность равного давления, т. е. такая поверхность, в каждой точке которой давление имеет постоянное значение.
Уравнение поверхности равного давления следует из основного уравнения равновесия жидкости. Так как для поверхности уровня р = const в любой ее точке, dр=0 и, следовательно, правая часть уравнения также равна нулю. Плотность жидкости отлична от нуля, поэтому выражение в скобках должно быть равным нулю, тогда уравнение поверхности уровня:
Поверхность уровня (поверхность равного давления) обладает двумя основными свойствами:
1. Поверхности уровня не пересекаются между собой. Действительно, предположив обратное, мы получим в точках линии пересечения этих поверхностей давление, равное одновременно р1 и р2, что физически невозможно. Следовательно, невозможно и пересечение поверхностей уровня.
2. Внешние массовые силы направлены по внутренней нормали к поверхности уровня.
📽️ Видео
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать
Откуда появляются дифференциальные уравнения и как их решатьСкачать
ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.Скачать
Урок 137. Движение тела в жидкости и газе.Скачать
Задача разделить 17 лошадейСкачать
Включи БОДРОСТЬ на Полную и Проживай Каждую Секунду на МАКСИМУМ!Скачать
Дифференциальные уравнения для самых маленькихСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
УДИВИТЕЛЬНЫЙ способ решения уравнения ★ Вы такого не видели! ★ Уравнение четвертой степениСкачать
Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
Решение физических задач с помощью дифференциальных уравненийСкачать
