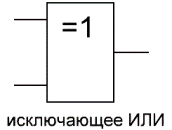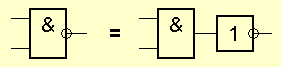Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
Логический элемент «И» — конъюнкция, логическое умножение, AND
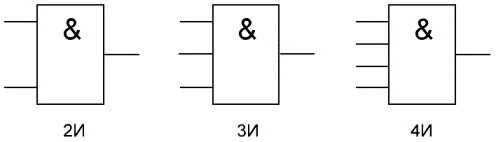
«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
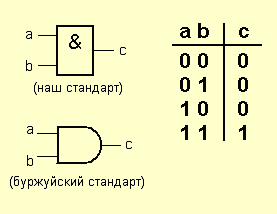
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.
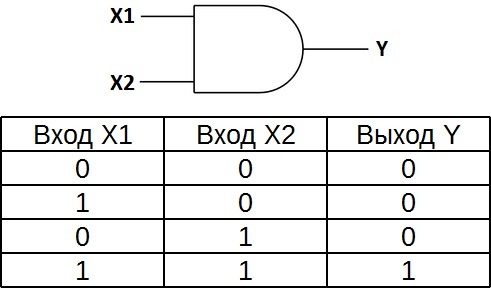
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR
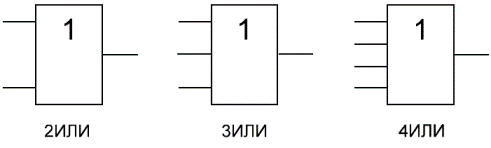
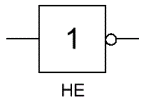
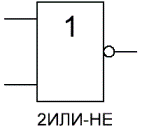
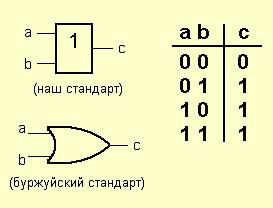
«ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
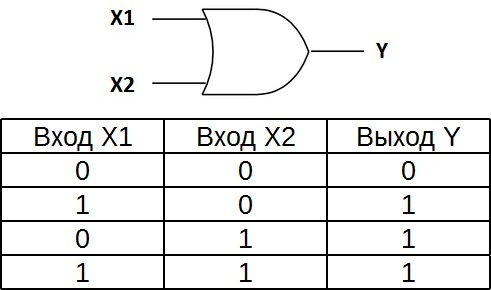
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».
Логический элемент «НЕ» — отрицание, инвертор, NOT
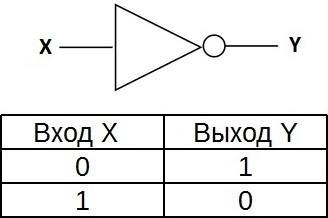
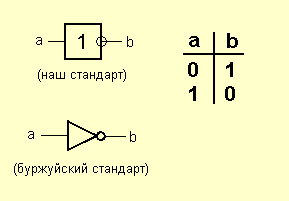
«НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND
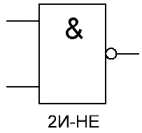
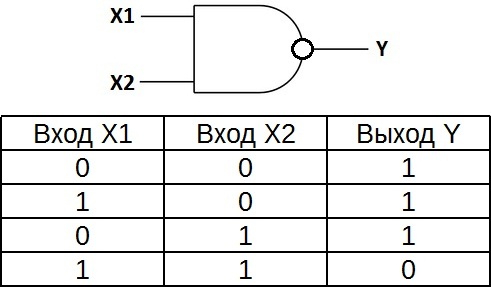
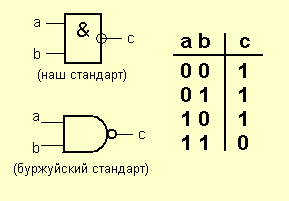
«И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR
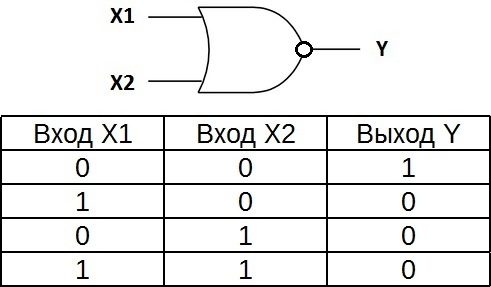
«ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR
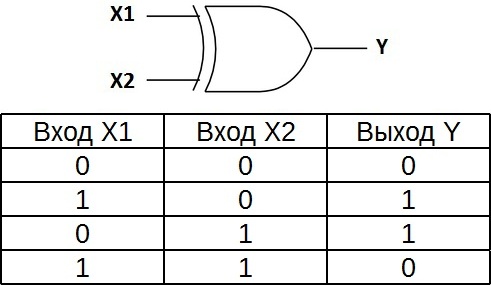
«исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход. Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.
Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Видео:Построение таблиц истинностиСкачать

Логические элементы и таблицы истинности
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.
Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Итак, какие бывают элементы?
Элемент «И» (AND)
Иначе его называют «конъюнктор».
Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.
Вот так выглядит элемент «И» и его таблица истинности:
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.
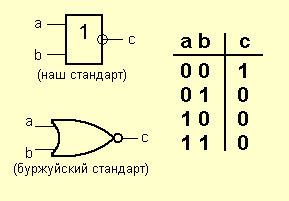
Элемент «ИЛИ» (OR)
По другому, его зовут «дизъюнктор».
Опять же, название говорит само за себя.
На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.
Элемент «НЕ» (NOT)
Чаще, его называют «инвертор».
Надо чего-нибудь говорить по поводу его работы?
Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».
Элемент «И-НЕ» (NAND)
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:
Элемент «ИЛИ-НЕ» (NOR)
Та же история – элемент «ИЛИ» с инвертором на выходе.
Следующий товарищ устроен несколько хитрее:
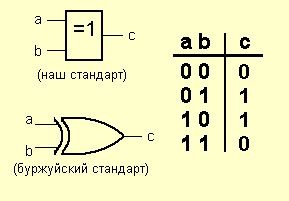
Элемент «Исключающее ИЛИ» (XOR)
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.
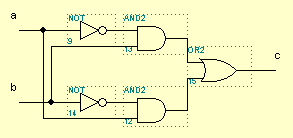
Эквивалентная схема примерно такая:
Ее запоминать не обязательно.
Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.
Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.
Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.
Видео:Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

Основы схемотехнической реализации ЭВМ
Системы логических элементов
Системой логических элементов называется функционально полный набор логических элементов, объединенных общими электрическими, конструктивными и технологическими параметрами и использующих одинаковый тип межэлементных связей [ 1 ] . Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также элементы для усиления, восстановления и формирования сигналов стандартной формы.
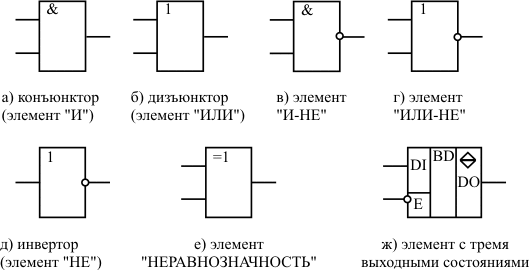
Условно-графические обозначения ( УГО ) некоторых логических элементов представлены на рис.13.1.
УГО элемента представляет собой прямоугольник , к которому слева подходят входные сигналы, а справа выходят выходные. Внутри прямоугольника ставится условное обозначение выполняемой элементом логической функции. Если значение выходного сигнала принимает инверсное значение по отношению к обозначенной внутри элемента функции, то данный выход обозначается на УГО элемента кружком (рис.13.1,в – 13.1,д). Аналогично, если активным уровнем входного сигнала является логический «0» , то данный вход обозначается кружком (вход E элемента 13.1,ж ).
Если элемент выполняет сложную функцию, имеет несколько функционально различных групп входов и выходов, то входы и выходы отделяются от основного поля УГО вертикальными линиями. Внутри каждого из получившихся полей функционально различные группы входов и выходов отделяются друг от друга горизонтальными линиями. На рис.13.1,ж показан элемент, выход которого может находиться в одном из трех состояний: логический «0» , логическая «1» , состояние высокого сопротивления. В состоянии высокого сопротивления выход элемента отключается от входов всех других элементов, с которыми он связан. Вход E ( enable ) этого элемента управляет состоянием его выхода. Так как на условно-графическом обозначении этот вход отмечен кружком, то отсюда следует, что функция разрешения передачи двоичного сигнала с входа на выход элемента выполняется при состоянии логического «0» на входе разрешения E . Если на вход E подан сигнал логической «1» , то выход элемента находится в отключенном (так называемом «третьем» ) состоянии.
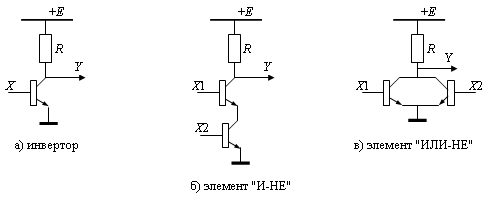
Каждый логический элемент – это электронно-техническое изделие (рис.13.2). В этих схемах все транзисторы работают в ключевом режиме. Это означает, что при подаче сигнала высокого уровня на базу транзистора, его сопротивление становится пренебрежимо малым, то есть транзистор как бы «стягивается в точку». При низком потенциале на базе транзистора сопротивление между коллектором и эмиттером становится чрезвычайно большим, что фактически означает разрыв цепи.
Рассмотрим это на примере работы инвертора (рис.13.2,а). Если сигнал X имеет высокий потенциал , то ключ , реализованный на транзисторе, замкнут, и потенциал точки Y низкий. В противном случае связь между точкой Y и «землей» разорвана, и сигнал Y имеет высокий уровень, что и обеспечивает реализацию логической функции » отрицание «.
Для элемента «И-НЕ» сигнал в точке Y будет иметь низкий уровень ( НУ ) лишь тогда, когда оба сигнала X1 и X2 имеют высокий уровень ( ВУ ). Работа этого элемента описывается таблицей 13.1.
| X 1 | X 2 | Y |
|---|---|---|
| НУ | НУ | ВУ |
| НУ | ВУ | ВУ |
| ВУ | НУ | ВУ |
| ВУ | ВУ | НУ |
Если принять, как это делается в наиболее распространенных сериях логических элементов, высокий уровень сигнала за логическую «1», а низкий уровень — за логический «0», то получим таблицу истинности данного элемента (таблицей 13.2).
| X 1 | X 2 | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Эта таблица соответствует логической функции «И-НЕ» .
В то же время, принимая высокий уровень сигнала за логический «0» , а низкий уровень – за логическую «1» , получим следующую таблицу истинности (табл. 13.3).
| X 1 | X 2 | Y |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Эта таблица соответствует уже функции «ИЛИ-НЕ» .
Таким образом, кодирование сигналов в системе логических элементов может влиять на выполняемую им логическую функцию. В дальнейшем будем полагать кодировку сигналов, принятую для табл. 13.2.
Для элемента «ИЛИ-НЕ» (см. рис.13.2) сигнал в точке Y будет иметь высокий уровень лишь тогда, когда оба сигнала X1 и X2 имеют низкий уровень. Работа этого элемента описывается табл. 13.4, а его таблица истинности при сделанных предположениях о кодировке сигнала – таблицей 13.5. Эта таблица соответствует логической функции «ИЛИ-НЕ» .
| X 1 | X 2 | Y |
|---|---|---|
| НУ | НУ | ВУ |
| НУ | ВУ | НУ |
| ВУ | НУ | НУ |
| ВУ | ВУ | НУ |
| X 1 | X 2 | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Параметры элементов принято делить на статические и динамические [ 1 ] . Статические параметры инвариантны к переходным процессам и измеряются в статическом режиме. Динамические, наоборот, определяют реактивные свойства элемента и измеряются во время переходных процессов.
К статическим параметрам относятся токи, текущие по выводам схемы, и соответствующие напряжения. Отметим среди этих параметров следующие:
- ток потребления;
- напряжение источника питания;
- пороговое напряжение низкого уровня ( U 0 );
- пороговое напряжение высокого уровня ( U 1 );
- потребляемая мощность;
- нагрузочная способность;
- помехоустойчивость.
Среди многочисленных динамических параметров , характеризующих схему, выделим следующие:
- время перехода при включении ( t 10 ) (задний фронт);
- время перехода при выключении ( t 01 ) (передний фронт);
- время задержки распространения при включении ( tзд 01 );
- время задержки распространения при выключении ( tзд 10 );
- среднее время задержки распространения ( tзд ср ) – интервал времени, равный полусумме времен задержки распространения сигнала при включении и при выключении; в дальнейшем это время будем называть временем задержки элемента ( tзд ).
Проиллюстрируем некоторые статические и динамические параметры логических схем на примере работы элемента «НЕ» (см. рис. 13.2,а). Временная диаграмма входного и выходного сигналов этого элемента, на которой отмечены его статические и динамические параметры , приведена на рис. 13.3.
Видео:Таблица истинностиСкачать

Раздел 2. Схемотехника цифровых устройств
Тема 2.1. Интегральные логические элементы
1.Понятие логической функции и логического устройства
2.Основные логические функции
3.УГО и таблицы истинности логических элементов
1. В цифровой технике для обозначения различной информации пользуются кодовыми словами. Для их построения используются символы 0 и 1, которые называют логический ноль (лог. 0) и логическая единица (лог. 1), соответственно.
Информация, которая передается между отдельными узлами сложного устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла поступают одни кодовые слова, а на выходе образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. При этом и функция, и ее аргументы могут принимать только значения лог.0 и лог.1. Такая функция называется логической функцией или функцией алгебры логики. Устройство, предназначенное для формирования функции алгебры логики, называется логическим устройством или цифровым устройством (ЦУ).
Логическую функцию можно задать следующими способами:
— словесно. Например, функция принимает значение лог. 1, если оба аргумента принимают значение лог. 1.
— таблично. Функция задается в виде таблицы, в которой приводятся все возможные наборы аргументов и соответствующие им значения функции. Такая таблица называется таблицей истинности.
— аналитически. Функция задается в виде логического выражения.
2. Существует множество логических функций. Основными из них являются следующие функции:
1. Логическое отрицание; инверсия; операция НЕ

2. Логическое сложение; дизъюнкция; операция ИЛИ
3. Логическое умножение; конъюнкция; операция И
4. Отрицание логического сложения; отрицание дизъюнкции; операция ИЛИ-НЕ;

5. Отрицание логического умножения; отрицание конъюнкции; операция И-НЕ;

6. Функция неравнозначности; сумма по модулю 2; операция исключающее «ИЛИ»

3. Логическое устройство, реализующее работу какой-либо логической функции, называется логическим элементом.
Общее условно-графическое обозначение (УГО) логических элементов:


* — функция, которую выполняет логический элемент.
Характеристики логических элементов:
— напряжение лог.0 и лог.1 (U 0 , U 1 );
— коэффициент объединения по входу – определяет количество входов элемента, по которым реализуется логическая функция;
— коэффициент разветвления по выходу (нагрузочная способность) – определяет количество входов аналогичных элементов, которые можно подключить к выходам данного;
— быстродействие – определяется максимальной задержкой распространения сигнала от входа к выходу tз = 0,5·(tз0,1 +tз1,0);
— помехоустойчивость – определяется максимальной величиной помехи, не вызывающей нарушения работы элемента.
Условно-графическое обозначение и таблицы истинности основных логических элементов:
элемент НЕ элемент ИЛИ элемент И




| х2 | х1 | х2vх1 |
| х2 | х1 | х2·х1 |
| х |  х х |
элемент ИЛИ-НЕ элемент И-НЕ элемент исключающее ИЛИ



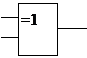


| х2 | х1 |  х2vх1 х2vх1 |
| х2 | х1 |  х2 v х1 х2 v х1 |
| х2 | х1 |  х2·х1 х2·х1 |
Тема 2.2. Комбинационные цифровые устройства
1.Шифратор и дешифратор
2.Мультиплексор и демультиплексор
3.Сумматоры
1. Шифратор – КЦУ, служащее для преобразования десятичного числа в двоичный код.
УГО шифратора Таблица истинности шифратора
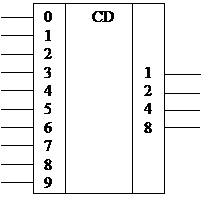 Десятичное число Десятичное число | Двоичный код 8421 | ||
| х8 | х4 | х2 | х1 |
Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша связана с определенным входом шифратора. При нажатии выбранной клавиши подается сигнал на соответствующий вход шифратора, и на его выходе возникает двоичное число, соответствующее выгравированному на клавише символу.
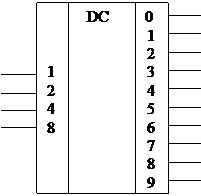
Дешифратор – КЦУ, служащее для преобразования двоичного кода в десятичное число.
УГО дешифратора Таблица истинности дешифратора
| Двоичный код 8421 | Десятичное число | ||
| х8 | х4 | х2 | х1 |
Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа и текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.
2.Мультиплексор – КЦУ, служащее для коммутации одного из информационных входов с выходом в соответствии с адресом.
УГО мультиплексора Таблица истинности мультиплексора
| Входы | Выход | |
| А0 | А1 | Q |
| * | * | |
| D0 | ||
| D1 | ||
| D2 | ||
| D3 |
Назначение выводов мультиплексора: D0 ÷ D3 – информационные входы
Q – информационный выход
При отсутствии стробирующего сигнала (С=0) связи между информационными входами и выходом нет. При С=1 на выход Q подключается вход D2, номер которого 2 соответствует двоичному коду на адресных входах 10.
Демультиплексор – КЦУ, служащее для коммутации информационного входа с одним из информационных выходов в соответствии с адресом.
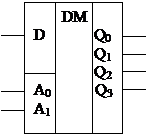
| Входы | Выходы | ||||
| А0 | А1 | Q0 | Q1 | Q2 | Q3 |
| D | |||||
| D | |||||
| D | |||||
| D |
Назначение выводов демультиплексора: D – информационный вход
Q0 ÷ Q3 – информационные выходы
3.Сумматор – КЦУ, служащее для алгебраического сложения двух двоичных чисел.
В зависимости от разрядности складываемых чисел сумматоры бывают одноразрядными и многоразрядными.
В зависимости от способа ввода двоичных слагаемых сумматоры делятся на два типа: последовательного и параллельного действия. В сумматоры первого типа слагаемые вводятся в последовательной форме, т.е. разряд за разрядом (младшим разрядом вперед), в сумматоры второго типа каждое из слагаемых подается в параллельной форме, т.е. одновременно всеми разрядами.
УГО одноразрядного Таблица истинности
двоичного сумматора одноразрядного двоичного сумматора
| Входы | Выходы | |||
| Слагаемые | Перенос | Сумма | Перенос | |
| ai | bi | pi | si | pi+1 |
Назначение выводов сумматора:
pi – вход переноса;
УГО многоразрядного сумматора
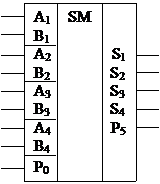
Тема 2.3. Последовательностные цифровые устройства
1. Общие сведения о триггерах
2. УГО, схемы, принцип работы триггеров
3. Общие сведения о регистрах
4. Регистры памяти и сдвига
5. Общие сведения о счетчиках
6. Суммирующий и вычитающий счетчики
1. Триггер – это ПЦУ, служащее для длительного хранения одного разряда двоичного числа.
Общее условно-графическое обозначение (УГО) триггера
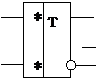
Триггер может находиться в одном из двух состояний: лог. 0 или лог. 1.

Триггеры имеют различные типы входов, которыми определяется наименование триггера. Различают четыре типа триггеров: RS-триггер, JK-триггер, D-триггер, T-триггер.
Интегральные триггеры реализуются на логических элементах И-НЕ, ИЛИ-НЕ.
По характеру реакции на входные сигналы триггеры бывают асинхронными и синхронными.
Асинхронный триггер реагирует на входные сигналы с момента их подачи на входы триггера. Такой триггер не имеет управляющего (синхронизирующего) входа С.
Синхронный триггер имеет управляющий (синхронизирующий) вход С и реагирует на входные сигналы только при подаче синхронизирующего сигнала на этот вход.
2. Асинхронный RS-триггер имеет два информационных входа: R – раздельный вход установки состояния лог. 0, S – раздельный вход установки состояния лог.1, и не имеет синхронизирующего входа.
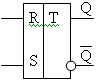
УГО RS-триггера Структура триггера Таблица истинности RS-триггера
на элементах ИЛИ-НЕ (бистабильная ячейка) на элементах ИЛИ-НЕ
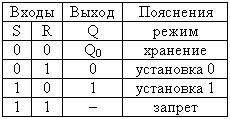
Асинхронный RS-триггер переключается с момента поступления сигналов на его входы. Если на вход R подан сигнал лог.1 (активный уровень для элемента ИЛИ-НЕ), то триггер устанавливается в состояние 0. Если на вход S подан сигнал лог.1 (активный для элемента ИЛИ-НЕ), то триггер устанавливается в состояние 1. Если на оба входа подаются сигналы лог.0 (пассивные уровни для элементов ИЛИ-НЕ), то триггер не изменяет своего состояния, т.е. находится в режиме хранения. Если на оба входа подаются сигналы лог.1 (активные уровни для элементов ИЛИ-НЕ), то на выходах триггера появятся одинаковые сигналы, что противоречит определению триггера (такую комбинацию подавать на входы триггера нельзя).
Синхронный D-триггер имеет два входа: информационный вход D – вход установки триггера в состояние, соответствующее логическому уровню на этом входе и синхронизирующий вход С.
УГО D-триггера Структура D-триггера
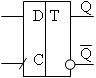 |  |
Таблица истинности Временные диаграммы
 | 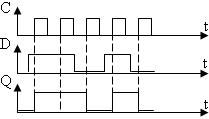 |
При наличии на входе C положительного фронта импульса D-триггер переключается в состояние, соответствующее уровню, действующему на входе D (если D=0, то Q=0; если D=1, то Q=1).
При отсутствии на входе C положительного фронта импульса D-триггер находится в режиме хранения.
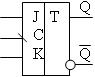
Синхронный Т-триггер имеет один вход Т – счетный вход.
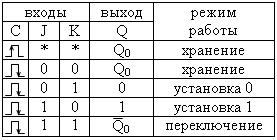
УГО триггера Таблица истинности триггера Временные диаграммы
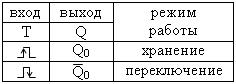 |
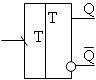 |
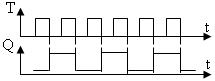 |
Т-триггер переключается в момент действия отрицательного фронта каждого импульса, поступающего на вход Т. Своими переключениями триггер как бы подсчитывает поступающие импульсы. Поэтому он называется счетным.
Синхронный JK-триггер имеет три входа: J – вход установки состояния лог.1, K – вход установки состояния лог.0, С – синхронизирующий вход. универсального триггера
УГО триггера Таблица истинности триггера
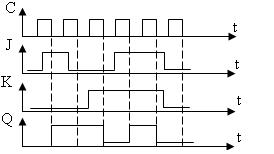
JK-триггер может использоваться в качестве двухступенчатого RS-триггера, D-триггера, Т-триггера, поэтому он называется универсальным.
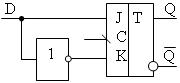
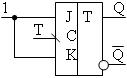
Использование JK-триггера в качестве:
3. Регистр – ПЦУ, служащее для записи, хранения, сдвига и выдачи многоразрядного двоичного числа.
Регистр строится в виде набора триггеров, каждый из которых предназначается для хранения цифр определенного числа. Таким образом, регистр для хранения n-разрядного двоичного числа должен содержать n триггеров. Одновременно регистр может хранить только одно слово.
Регистры строятся на основе RS, JK, D-триггеров.
В зависимости от способа ввода и вывода двоичного числа регистры могут быть:
Параллельные регистры называются также регистрами памяти, остальные регистры являются регистрами сдвига.
УГО универсального регистра

D0 ÷ D7 – информационные входы при
DR, DL – информационные входы при
S0, S1 – входы выбора режима работы
R – вход установки нуля;
Q0 ÷ Q7 – информационные выходы.
4. В параллельных регистрах ввод и вывод двоичного числа осуществляется одновременно всеми разрядами. Такие регистры могут только хранить двоичное число, поэтому называются регистрами памяти.
Схема регистра памяти на D – триггерах
Двоичное число поступает на входы D триггеров регистра одновременно всеми разрядами. В момент действия на входе C положительного фронта импульса число записывается в регистр, а затем он переходит в режим хранения.
Регистры, в которых ввод и/или вывод информации осуществляется последовательно, называются регистрами сдвига.
Суть сдвига заключается в перезаписи двоичного разряда из одного триггера в другой (соседний). Если перезапись разряда происходит из старшего разряда в младший, то осуществляется сдвиг вправо; если перезапись происходит из младшего разряда в старший, то осуществляется сдвиг влево.
Схема четырехразрядного регистра сдвига вправо на D – триггерах
Схема четырехразрядного регистра сдвига влево на D – триггерах
5. Счетчик – ПЦУ, служащее для счета импульсов, поступающих на его вход.
Счетчики строятся на основе JK и Т-триггеров. Если в схему счетчика входит n триггеров, то счетчик является n-разрядным.
— коэффициент счета (Ксч) – число импульсов, после поступления которых на вход счетчика он переключается в исходное состояние. Коэффициент счета зависит от разрядности счетчика n и определяется по формуле Ксч= 2 n ;
— емкость счетчика – максимальное число импульсов, которое может сосчитать счетчик за один полный цикл счета;
— быстродействие – определяется временем переключения триггеров и скоростью передачи переноса между разрядами.
По направлению счета:
— суммирующий (счет идет в возрастающем порядке);
— вычитающий (счет идет в убывающем порядке);
— реверсивный (счет может вестись как в возрастающем, так и в убывающем порядке).
По порядку изменения состояний:
— с естественным порядком счета (соседние состояния счетчика отличаются на единицу);
— с произвольным порядком счета (соседние состояния счетчика отличаются более чем на единицу).
По коэффициенту счета:
— двоичные (Ксч= 2 n );
— 
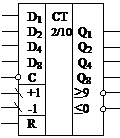
С – вход разрешения предварительной записи;
+1, –1 – счетные входы при работе счетчика в суммирующем и
вычитающем режимах, соответственно;
R – вход установки нуля;
≥9, ≤0 – выходы переноса при работе счетчика в суммирующем и
вычитающем режимах, соответственно.
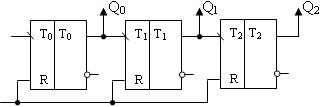
6. Счетчик, в котором счет идет в возрастающем порядке, называется суммирующим. Триггеры в таком счетчике соединяются следующим образом: прямой выход младшего триггера со счетным входом старшего триггера. Информация о состоянии счетчика снимается с прямых выходов триггеров.
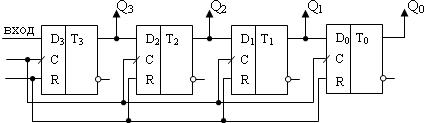
Схема трехразрядного суммирующего счетчика Таблица истинности счетчика

Счетчик, в котором счет идет в убывающем порядке, называется вычитающим. Триггеры в таком счетчике соединяются следующим образом: обратный выход младшего триггера со счетным входом старшего триггера. Информация о состоянии счетчика снимается с прямых выходов триггеров.
Схема трехразрядного вычитающего счетчика Таблица истинности счетчика

📹 Видео
Построение схем по логическим выражениямСкачать

8 класс. Логические элементыСкачать

Конъюнкция, Дизъюнкция, Инверсия, Отрицание, Импликация, Следование. Таблица истинностиСкачать

Логические элементы | Информатика 8 класс #16 | ИнфоурокСкачать

Построение логических схемСкачать

ИНФОРМАТИКА 8 класс: Построение таблиц истинности для логических выраженийСкачать

Логические элементы | Информатика 9 класс #4 | ИнфоурокСкачать

Информатика. Алгебра логики: Таблицы истинности. Центр онлайн-обучения «Фоксфорд»Скачать

Информатика 8 класс (Урок№6 - Таблицы истинности. Контрольная работа.)Скачать

Построение логических схемСкачать

Элементы ИЛИ, И, НЕ в логических схемах РЗАСкачать

Математика это не ИсламСкачать

Логические элементы И, ИЛИ, Исключающее ИЛИ. История, Теория, Применение.Скачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

4 1 9 Составление таблиц истинности для логических схемСкачать

Разбор построение логических схемСкачать
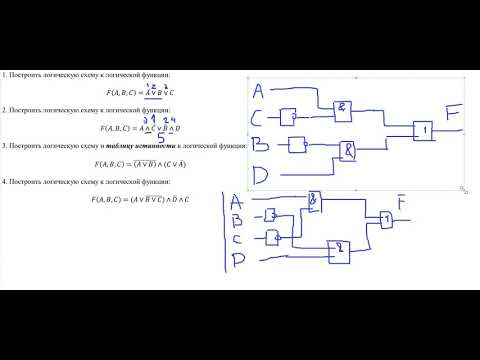
Информатика 8 класс. Логические элементы (УМК Босов Л.Л., Босова А.Ю.)Скачать