- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Анализ временных рядов
- Прогноз, характеристики и параметры прогнозирования
- Уравнение тренда временного ряда
- 9.6. Методика измерения параметров тренда
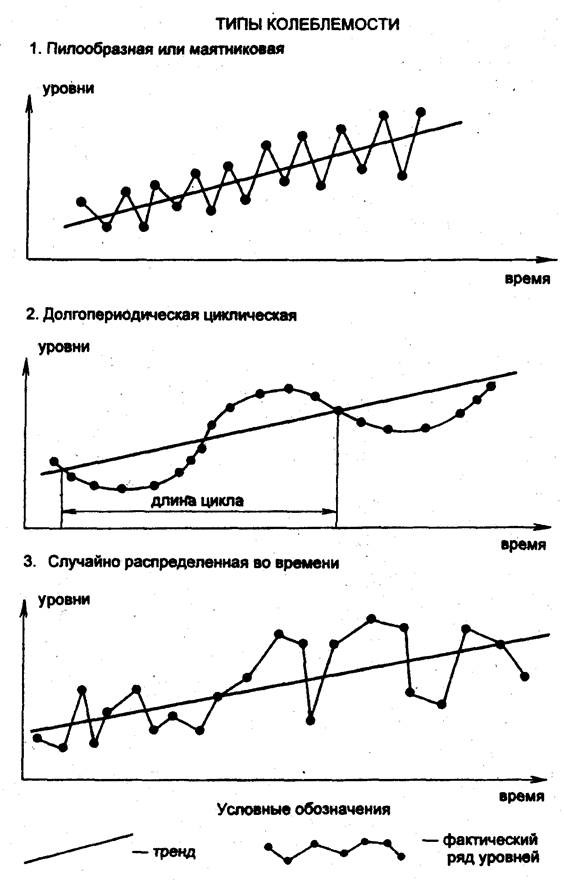
- 9.7. Методика изучения и показатели колеблемости
- 9.8. Измерение устойчивости в динамике
- 5 способов расчета значений линейного тренда в MS Excel
- Добавление трендовой линии на график
- Построение графика
- Создание линии
- Настройка линии
- Прогнозирование
- Базовые понятия
- Определение коэффициентов модели
- Способ расчета значений линейного тренда в Excel с помощью графика
- Способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
- Уравнение линии тренда в Excel
- Линейная аппроксимация
- Экспоненциальная линия тренда
- Логарифмическая линия тренда в Excel
- Общая информация
- Возможности инструмента
- Разновидности
- Разбираемся с трендами в MS Excel
- Зачем нужна линия тренда
- Как построить линию тренда в MS Excel
- 🎬 Видео
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 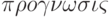
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
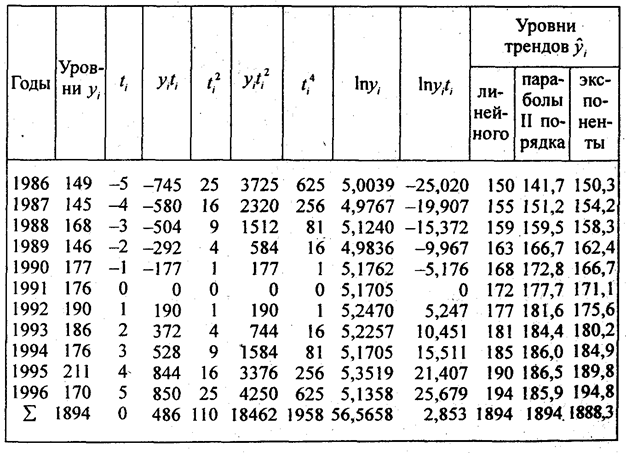
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 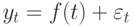

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
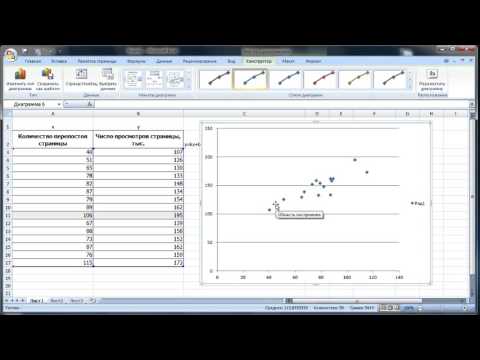
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 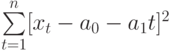
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
 | 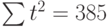 | 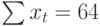 | 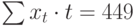 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
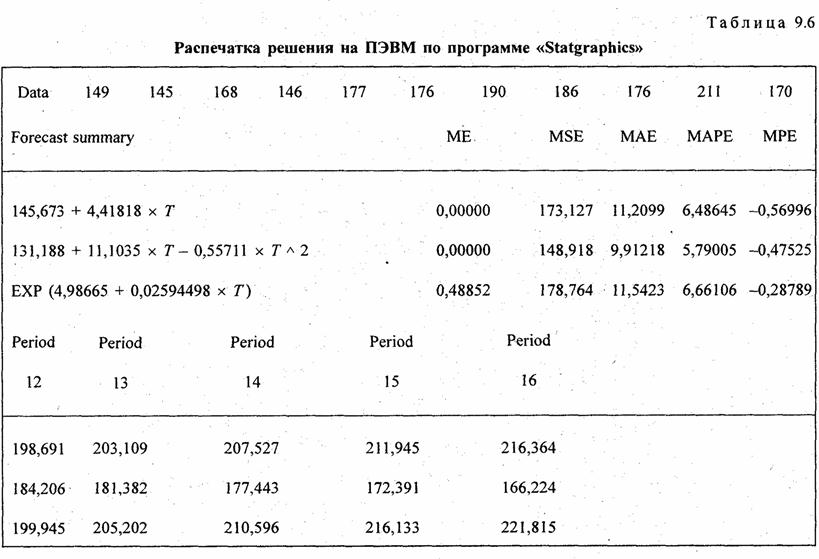
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

| 23.01.2012, 17:50 | |||||||||||||||
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Общая информация
Линия тренда – это инструмент статистического анализа, который позволяет спрогнозировать дальнейшее развитие событий. Чтобы построить кривую, необходимо иметь массив данных, который отображает изменение величины во времени. На основании этой информации строится график, а затем применятся специализированная функция. Рассмотрим изменение цены золота за грамм в долларах с 2015 по 2019 год.
- Составляете небольшую таблицу.
- На основании этих данных строите линейный график. Для этого переходите во вкладку Вставка на Панели инструментов и выбираете нужный тип диаграммы.
- Получается некоторая кривая.
- Необходимо отредактировать график при помощи стандартных инструментов, которые находятся во вкладках Конструктор, Макет и Формат. Переименовываете диаграмму, выставляете пределы по вертикальной оси, чтобы изменения величины были более явными, подписываете оси, добавляете контрольные точки, а также подпись данных. После этого проводите окончательное форматирование.
- Чтобы добавить линию тренда, необходимо во вкладке Макет нажать одноименную кнопку и выбрать нужный тип приближения.
На заметку! Если линия тренда не активна, то используется не тот тип диаграммы. Данная функция работает только с диаграммами типа гистограмма, график, линейчатая и точечная.
6. Так выглядит линия тренда на графике.
На заметку! Построение линии приближения идентично для редакторов 2007, 2010 и 2016 годов выпуска.
Видео:Лекция 3. Экспоненциальное сглаживание.Методы Брауна, Хольта-Винтерса.Оценка параметров сглаживания.Скачать

Возможности инструмента
Рассмотрим подробнее настройки функции. Для перехода в окно параметров из выпадающего списка нужно выбрать последнюю строчку.
Окно содержит четыре настройки, в которые входят цвет, объем и тип линии, а также параметры самого инструмента.
Параметры линии тренда можно условно поделить на четыре блока:
- Тип приближения.
- Название полученной кривой, которое формируется автоматически или может быть задано пользователем.
- Блок прогнозирования, который позволяет продлить линию тренда на заданное количество периодов вперед или назад, на основании имеющихся данных. Что позволяет оценить дальнейшее изменение исследуемой величины.
- Дополнительные опции, которые отражают математическую составляющую кривой. Самой интересной и полезной строчкой здесь является величина достоверности. Если значение коэффициента близко к единице, то ошибка минимальна и дальнейший прогноз будет достаточно точным.
Выведем на исходный график уравнение линии и коэффициент достоверности.
Как видите, значение близко к 0,5, это говорит о низкой достоверности полученной линии тренда, и дальнейший прогноз будет ошибочным.
Видео:Аппроксимация в ExcelСкачать

Разновидности
1 Линейная аппроксимация отлично подойдет для исследования величины, которая стабильно растет или убывает. Тогда кривая будет иметь вид прямой. Формула будет содержать одну переменную. Коэффициент достоверности близок к единице, что говорит о высокой точности совпадения прямой и массива данных. На основании такой линии тренда прогноз будет достаточно точным.
2. Экспоненциальная кривая используется только для массивов с положительными значениями, которые изменяются непрерывно.
3. Логарифмическую линию тренда целесообразнее использовать, если на первоначальном этапе наблюдается резкое увеличение или снижение показателя, а потом наступает период стабильности. Здесь формула содержит логарифм натуральный.
4. Полиномиальная аппроксимация применяется при большом количестве неоднородных данных. В основе лежит степенное уравнение, при этом количество степеней зависит от числа максимумов. Применим этот тип для первоначального примера с золотом.
Уравнение показывает переменные до третьей степени, поскольку график имеет два пика. Также видим, что коэффициент достоверности близок к единице (вместо 0,5 при линейной аппроксимации), значит линия тренда выбрана правильно и дальнейший прогноз будет точным.
Как видите, для статистического анализа данных необходимо правильно выбрать тип математического уравнения, которое максимально точно будет соответствовать характеру изменения величины. На основании полученных кривых можно осуществлять прогноз, подставляя в уравнение необходимое число.
Видео:Аналитическое выравниваниеСкачать

Разбираемся с трендами в MS Excel
Большой ошибкой со стороны владельца сайта будет воспринимать диаграмму как есть. Да, невооруженным взглядом видно, что синий и оранжевый столбики «осени» выросли по сравнению с «весной» и тем более «летом». Однако важны не только цифры и величина столбиков, но и зависимость между ними. То есть в идеале, при общем росте, «оранжевые» столбики просмотров должны расти намного сильнее «синих», что означало бы то, что сайт не только привлекает больше читателей, но и становится больше и интереснее.
Что же мы видим на графике? Оранжевые столбики «осени» как минимум ни чем не больше «весенних», а то и меньше. Это свидетельствует не об успехе, а скорее наоборот — посетители прибывают, но читают в среднем меньше и на сайте не задерживаются!
Самое время бить тревогу и… знакомится с такой штукой как линия тренда .
Видео:Парная и множественная линейная регрессияСкачать
Зачем нужна линия тренда
Линия тренда «по-простому», это непрерывная линия составленная на основе усредненных на основе специальных алгоритмов значений из которых строится наша диаграмма. Иными словами, если наши данные «прыгают» за три отчетных точки с «-5» на «0», а следом на «+5», в итоге мы получим почти ровную линию: «плюсы» ситуации очевидно уравновешивают «минусы».
Исходя из направления линии тренда гораздо проще увидеть реальное положение дел и видеть те самые тенденции, а следовательно — строить прогнозы на будущее. Ну а теперь, за дело!
Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Как построить линию тренда в MS Excel
Щелкните правой кнопкой мыши по одному из «синих» столбцов, и в контекстном меню выберите пункт «Добавить линию тренда» .
На листе диаграммы теперь отображается пунктирная линия тренда. Как видите, она не совпадает на 100% со значениями диаграммы — построенная по средневзвешенным значениям, она лишь в общих чертах повторяет её направление. Однако это не мешает нам видеть устойчивый рост числа посещений сайта — на общем результате не сказывается даже «летняя» просадка.
Линия тренда для столбца «Посетители»
Теперь повторим тот же фокус с «оранжевыми» столбцами и построим вторую линию тренда. Как я и говорил раньше: здесь ситуация не так хороша. Тренд явно показывает, что за расчетный период число просмотров не только не увеличилось, но даже начало падать — медленно, но неуклонно.
Ещё одна линия тренда позволяет прояснить ситуацию
Мысленно продолжив линию тренда на будущие месяцы, мы придем к неутешительному выводу — число заинтересованных посетителей продолжит снижаться. Так как пользователи здесь не задерживаются, падение интереса сайта в ближайшем будущем неизбежно вызовет и падение посещаемости.
Следовательно, владельцу проекта нужно срочно вспоминать чего он такого натворил летом («весной» все было вполне нормально, судя по графику), и срочно принимать меры по исправлению ситуации.
🎬 Видео
Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

Excel для полных чайников Урок 16 Линия трендаСкачать
Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Эконометрика. Моделирование временных рядов. Построение аддитивной модели.Скачать


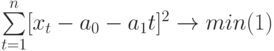
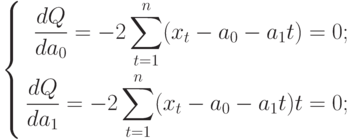
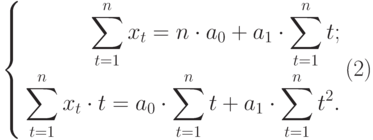
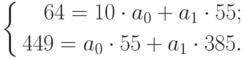




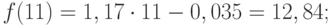
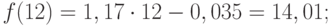
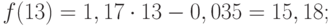
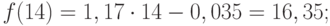
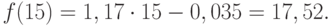


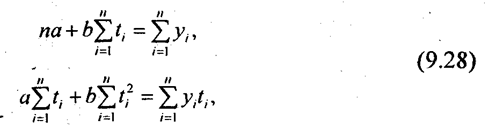



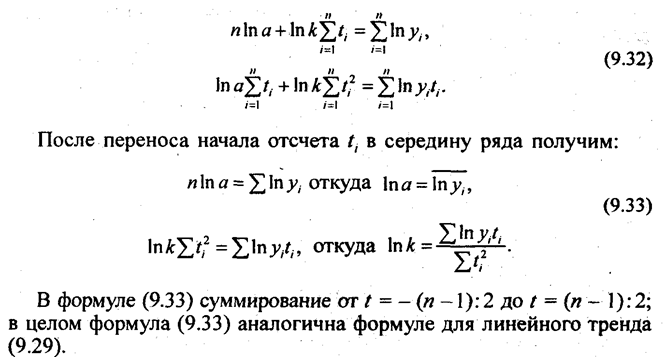
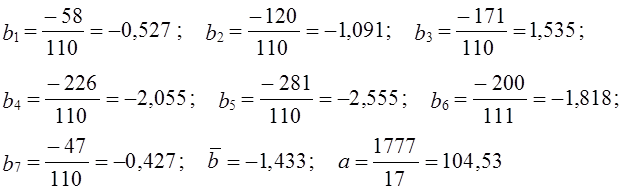

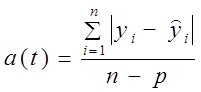 (9.34)
(9.34)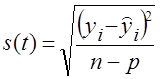 (9.35)
(9.35)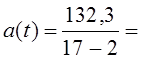 =8,82 пункта.
=8,82 пункта.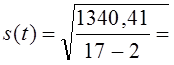 = 9,45 пункта.
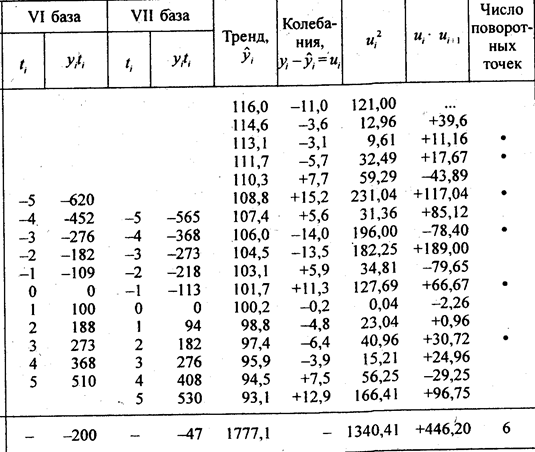
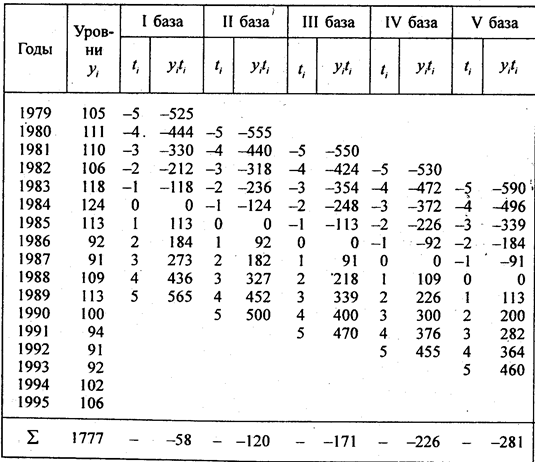
= 9,45 пункта.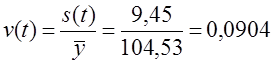 или 9,04%. Колеблемость умеренная, не сильная. Для сравнения приводим показатели (без расчета) по колебаниям урожайности картофеля, данные таблиц 9.1 и 9.5 — отклонение от линейного тренда:
или 9,04%. Колеблемость умеренная, не сильная. Для сравнения приводим показатели (без расчета) по колебаниям урожайности картофеля, данные таблиц 9.1 и 9.5 — отклонение от линейного тренда: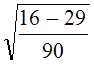 , в нашем случае
, в нашем случае 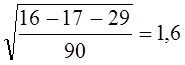 .
.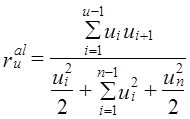 (9.36)
(9.36)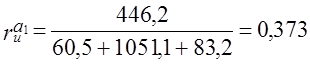

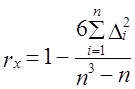



 Чтобы правильно строить трендовые линии, нужно соблюдать функциональную зависимость y=f(x) . Для получения корректного прогноза в столбец А вносится информация о временном периоде, а в столбец В — цена в указанный промежуток.
Чтобы правильно строить трендовые линии, нужно соблюдать функциональную зависимость y=f(x) . Для получения корректного прогноза в столбец А вносится информация о временном периоде, а в столбец В — цена в указанный промежуток. Построение графика выполняется по следующему алгоритму:
Построение графика выполняется по следующему алгоритму:

 Однако важно помнить, что вставить линию нельзя для диаграмм и графиков следующего типа:
Однако важно помнить, что вставить линию нельзя для диаграмм и графиков следующего типа:
 Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.). Для этого выполняем последовательность действий:
Для этого выполняем последовательность действий:




 Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У – объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044
Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У – объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044























