3 как найти все корни квадратного уравнения используя надстройку подбор параметра (2 видео)

Задача: Найти корни уравнения с помощью подбора параметра

Так как мы ищем корни полинома третьей степени, то имеются не более трех вещественных корней.

Для нахождения корней их первоначально нужно локализовать, т.е. найти интервалы, на которых эти корни существуют. Такими интервалами служат промежутки, на которых функция меняет знак. Для нахождения этих интервалов нужно построить график функции или ее протабулировать .

Протабулируем функцию на интервале [-1;1]. В ячейку А 1 вводим: -1, в ячейку А2:-0,8; протягиваем маркер заполнения.

В ячейку B 2 введем значение функции:
Протягиваем маркер заполнения.
Устанавливаем точность, с которой находится корень. Выбрать команду Сервис– Параметры–вкладку Вычисления. Устанавливаем Относительная погрешность –0,00001 и Предельное число итераций – 1000.
Полином меняет знак на интервалах [-1;-0,8],[0,2;0,4] и [0,6;0,8], поэтому на каждом из этих интервалов имеется свой корень. Так как полином третьей степени имеет не более трех корней, то все они и локализированы.
В ячейку С 2 вводим начальное приближение к корню уравнения, после применения подбора параметра в ней будет находиться найденное приближенное значение корня. За начальное приближения к корню можно взять среднюю точку отрезков локализации корня. С 2 =-0,9; С3=0,3; С4=0,7.
В ячейки D 2, D 3, D 4 вводим значение функции, за неизвестное указывается ячейка, отведенная под искомый корень С 2 , С3, С4 соответственно.
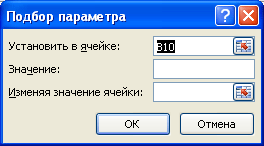
Выбираем команду Сервис– Подбор параметра. В диалоговом окне Подбор параметра в поле У становить в ячейке вводим ссылку на ячейку, в которой введена формула, вычисляющая значение левой части уравнения. Для нахождения корня с помощью подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную.
В поле Значение вводим 0. Здесь указывается значение из правой части уравнения.
В поле И зменяя значения ячейки вводим С2. В этом поле приводится ссылка на ячейку, отведенную под переменную. Нажать OK .
Аналогично находятся два оставшихся корня.

Содержание

Подбор параметра в EXCEL
Простейший пример
Калькуляция, подбираем значение прибыли
Подбор суммы кредита
Уравнения и задачи на подбор параметра в Excel
Подбор параметра и решение уравнений в Excel
Второй пример использования подбора параметра для уравнений
🎬 Видео

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Подбор параметра в EXCEL

history 18 ноября 2012 г.

Другие Стандартные Средства

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .

Видео:Решить простейшее уравнение. MS Excel. Подбор параметраСкачать

Простейший пример

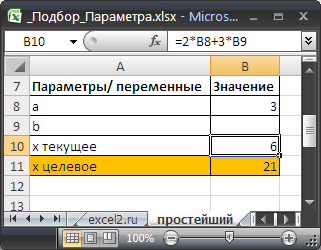
Найдем значение параметра b в уравнении 2*а+3*b=x , при котором x=21 , параметр а= 3 .

Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9 . В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x ). Целевое значение x в ячейке B11 введено для информации.

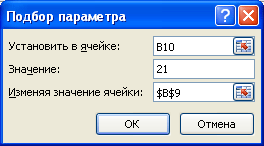
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …) .

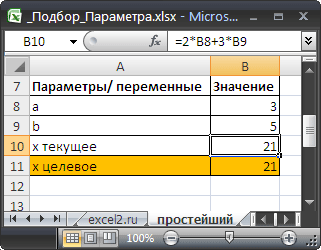
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b ).

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно .

Примечание : Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b , которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший .

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Видео:Excel. Подбор параметра.Скачать

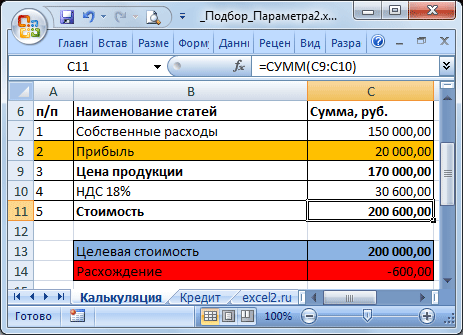
Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13 ). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли ( С8 ), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение ( С14 ) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11 ) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра .

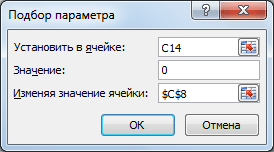
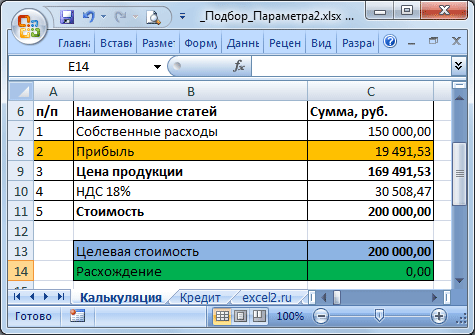
Выделите ячейку С14 , вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Видео:решаем квадратные уравнения в ExcelСкачать

Подбор суммы кредита

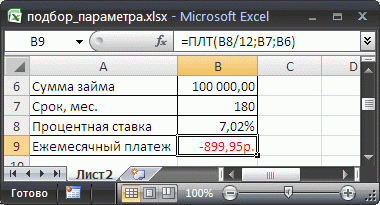
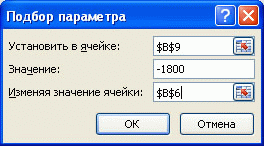
Предположим, что нам необходимо определить максимальную сумму кредита , которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет ). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

Введем в ячейку B 6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B 7 , % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …;
в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9 ;
введите искомый результат в поле Значение . В данном примере он равен -1800 ;
В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6 ;
Нажмите ОК

Что же сделал Подбор параметра ? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения . Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.

Видео:Excel Подбор параметра. Решение математических уравненийСкачать

Уравнения и задачи на подбор параметра в Excel

Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.

Видео:Решение уравнений в Excel используя инструмент Подбор параметраСкачать

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

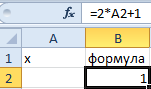
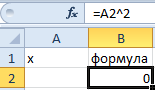
y =7 является функцией x ;
нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

Заполните ячейки листа, так как показано на рисунке:
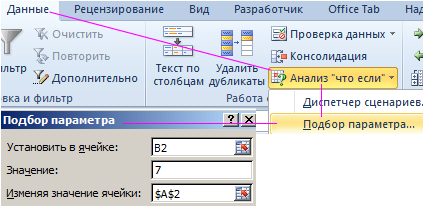
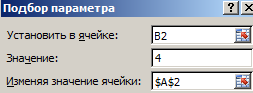
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

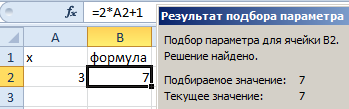
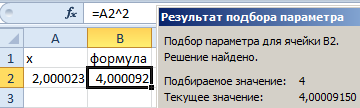
В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Видео:Решение уравнения в Excel. Используется средство "Подбор параметра"Скачать

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

Заполните ячейку B2 формулой как показано на рисунке:
Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
Сравните 2 результата вычисления:

Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.

Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:

Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.

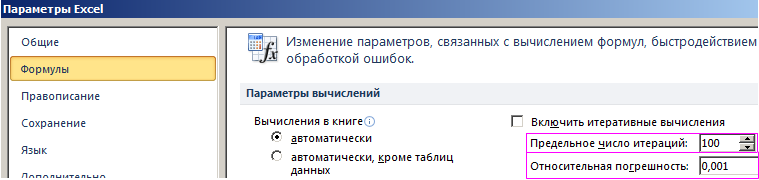
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.