3 из каких предпосылок выводится уравнение ван дер ваальса

Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).

Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)

постоянная b учитывает собственный мольный объем молекул.

При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления (иногда его называют статическим давлением). Изначально величина была учтена в общей форме в уравнении Гирна (1865)

(p + ) (V – nb) = nRT. (1.4)

Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:

(1.5)

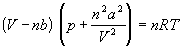
или для одного моля

. (1.6)

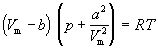
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.

Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов

Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление

(1.7)

(1.8)

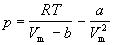
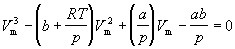
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.

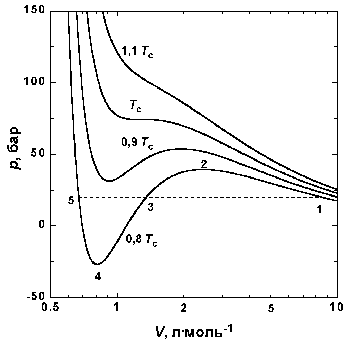Рис.1.4 Изотермы Ван-дер-Ваальса для СО2

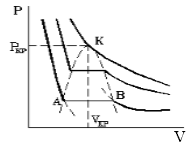
На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы 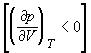. Состояния на участках 12 и 54, которые соответствуют переохлажденному пару и перегретой жидкости, соответственно, являются неустойчивыми (метастабильными) и могут быть лишь частично реализуемы в специальных условиях. Так, осторожно сжимая пар выше точки 1 (рис. 1.4), можно подняться по кривой 12. Для этого необходимо отсутствие в паре центров конденсации, и в первую очередь пыли. В этом случае пар оказывается в пересыщенном, т.е. переохлажденном состоянии. И наоборот, образованию капелек жидкости в таком паре способствуют, например, попадающие в него ионы. Это свойство пересыщенного пара используется в известной камере Вильсона (1912), применяемой для регистрации заряженных частиц. Движущаяся заряженная частица, попадая в камеру, содержащую пересыщенный пар, и соударяясь с молекулами, образует на своем пути ионы, создающие туманный след – трек, который фиксируется фотографически.

Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.

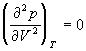
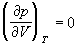
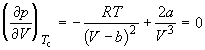
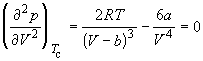
По мере повышения температуры все три корня сближаются, и при критической температуре T_c все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [] с горизонтальной касательной [], то есть

, (1.9)

. (1.10)

Совместное решение этих уравнений дает:

, (1.11)

, (1.12)

, (1.13)

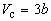
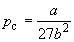
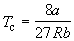
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Z_c для всех газов должен быть равен

(1.14)

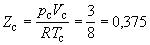
Из таблицы 1.2 видно, что хотя значение Z_c для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.

Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;

2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);

3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).

Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Содержание

1. Уравнение Ван-дер-Ваальса
2. Что такое реальный газ
3. Уравнение Ван-дер-Ваальса
4. Готовые работы на аналогичную тему
5. 2.5. Уравнение Ван-дер-Ваальса
6. 🌟 Видео

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Уравнение Ван-дер-Ваальса

Вы будете перенаправлены на Автор24

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Что такое реальный газ

Реальным газом называют газ, между молекулами которого существуют заметные силы взаимодействия. В неидеальных, газах под высоким давлением, газах с большой плотностью взаимодействие молекул велико и его необходимо учитывать. Силы притяжения играют наиболее существенную роль на больших расстояниях между молекулами. Расстояние уменьшается, силы притяжения растут, но до определенного предела, затем они начинают уменьшаться и переходят в силы отталкивания. Притяжение и отталкивание молекул можно разделить и рассматривать и учитывать отдельно друг от друга.

Видео:Уравнение Ван дер ВаальсаСкачать

Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса, описывающее состояние 1 моля реального газа, имеет вид:

где d- диаметр молекулы,

величина a вычисляется по формуле:

где $W_pleft(rright)$- потенциальная энергия притяжения двух молекул. Необходимо заметить, что газовая постоянная имеет индивидуальное значение для каждого вещества. Она отличается от молярной газовой постоянной, причем она меньше, что говорит об объединении молекул вещества в комплексы около критического состояния. Вдали от критических состояний можно использовать универсальную газовую постоянную.

С увеличением объема роль поправок в уравнении (1) становится менее существенной. И в пределе уравнение (1) переходит в уравнение состояния идеального газа для 1 моля (4):

Уравнение (4) — уравнение Менделеева — Клайперона, где m- масса газа, $R=8,31 frac$- универсальная газовая постоянная.

Это согласуется с тем фактом, что при уменьшении плотности реальные газы по своим свойствам приближаются к идеальным.

Уравнение (1) может быть записано в вириальной форме:

Для анализа изотерм уравнение (1) удобнее представить в виде:

Рассматриваемое уравнение может описывать и свойства жидкости, например плохую ее сжимаемость.

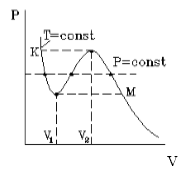
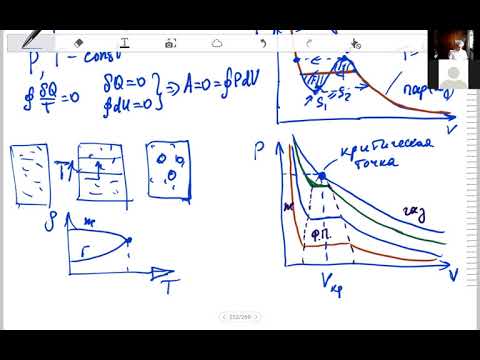
На рис.1 изображена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, построенная из соответствующего уравнения.

Такая зависимость на практике невозможна. Опыт показывает, что график должен иметь вид рис.2 то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V (рис 2). Это область фазового перехода. Жидкость и газ существую одновременно.

По мере увеличения температуры участок, отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V), сужается и превращается в точку (рис. 2). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.

Готовые работы на аналогичную тему

Итак, уравнение Ван-дер-Ваальса описывает поведение газов близких к реальным. Их можно применить к газообразной и жидкой фазам вещества. Эти уравнения отражают существование фазового перехода газ — жидкость. Показывают наличие критической точки перехода. Однако абсолютно точных количественных результатов расчеты, в которых используются вышеназванные уравнения, не дают.

Задание: Газ в количестве 1 моль находится в сосуде объемом V л при температуре $T_1$ давление газа $p_1$, а при $T_2$ давление газа $p_2$. Найти постоянные Ван-дер-Ваальса.

Запишем уравнение Ван-дер-Ваальса для одного моля реального газа для состояний 1 и 2:

Раскроем скобки в (1.1):

Вычтем $left(1.4right). из left(1.3right):$

Выразим a из (1.1):

Задание: Для реального газа, используя уравнение Ван-дер-Ваальса, получите уравнение адиабаты в параметрах V и T.

[delta Q=dU+partial A=0 left( 2.1right)]

Так как процесс адиабатный, то он идет теплообмена. Перепишем уравнение (2.1) для ван-дер-ваальсовского газа, зная, что:

Из уравнения Ван-дер-Ваальса:

Подставим (2.5) в (2.4), разделим переменные:

Ответ: Уравнение адиабаты для заданного случая имеет вид: $^<fracnu >T=const.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15.01.2022

Видео:Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

2.5. Уравнение Ван-дер-Ваальса

Уравнение Клапейрона — Менделеева следует из молекулярно-кинетической теории в предположении идеальности газа. Если мы хотим описывать поведение реальных систем, надо учесть взаимодействие молекул между собой. Точный учет межмолекулярных сил — задача чрезвычайно трудная. Поэтому было предложено несколько модификаций уравнения состояния идеального газа, которые могли бы учесть основные особенности реальных систем. Наиболее удачной попыткой стало уравнение Ван-дер-Ваальса, при получении которого вносились поправки в уравнение состояния идеального газа

В подходе Ван-дер-Ваальса, во-первых, принимается во внимание, что молекулы имеют конечные размеры. Если обозначить собственный объем всех молекул в моле вещества буквой b, то для движения молекул остается свободный объем

и именно он должен фигурировать в уравнении состояния. Во-вторых, учитывается, что молекула, подлетающая к стенке сосуда, «чувствует» притяжение других молекул, которое уравновешивалось, когда молекула была внутри сосуда. Дополнительная сила, направленная внутрь сосуда, эквивалентна дополнительному давлению p_i, (его называют «внутренним» давлением газа). Поэтому вместо давления р газа на стенки сосуда уравнение состояния должно содержать сумму р+р_i.

Как зависит внутреннее давление p_i от параметров системы? Сила, действующая на каждую молекулу, пропорциональна концентрации п молекул в системе. Число подлетающих к стенке молекул также пропорционально п, и потому внутреннее давление пропорционально квадрату концентрации частиц:

Обозначая коэффициент пропорциональности буквой а, приходим к уравнению Ван-дер-Ваальса

Для одного моля вещества это уравнение упрощается:

🌟 Видео

Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Теплофизика Л8. Реальные газы. Уравнение Ван дер Ваальса для приведенных величинСкачать

Урок 195. Изотермы реального газаСкачать

Лекция №7 "Газ Ван-дер-Ваальса. Эффект Джоуля-Томсона" (Овчинкин В.А.)Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

270. Силы Ван-дер-ВаальсаСкачать

Силы Ван-дер-Ваальса (видео 1) | Силы межмолекулярного взаимодействия | ХимияСкачать

Закон БернуллиСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

1 3 Водородная связь Ван дер Ваальсовы силыСкачать

Физическая Химия газ Ван дер Ваальса №3 #physicalchemistryСкачать

Одно уравнение и 3 неизвестныхСкачать

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать