3 е и 4 е уравнения максвелла выражаются формулами

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Видео:3 14 Уравнения МаксвеллаСкачать

Третье и четвертое уравнения Максвелла

Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности:

, (1.40)

где dS = n0dS; n0 – орт внешней нормали к поверхности S.

До Максвелла уравнение (1.40) рассматривалось только в применении к постоянным полям. Максвелл предположил, что оно справедливо и в случае переменных полей.

Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае

, (1.41)

где ρ – объемная плотность зарядов; V—объем, ограниченный поверхностью S. Объемная плотность зарядов

, (1.42)

где ΔQ – заряд, сосредоточенный в объеме ΔV. Размерность ρ – кулон на кубический метр (Кл/м3).

Подставляя (1.41) в (1.40), получаем

. (1.43)

Уравнение (1.43) обычно называют третьим уравнением Максвелла в интегральной форме. Для перехода к диффе­ренциальной форме преобразуем левую часть этого уравнения по теореме Остроградского-Гаусса (П. 19). В результате получим:

.

Это равенство должно выполняться при произвольном объеме V, что возможно только в том случае, если

Соотношение (1.44) принято называть третьим уравнением Максвелла. В декартовой системе координат оно записывается в виде

.

Из равенства (1.44) следует, что дивергенция вектора D отлична от нуля в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора D начинаются на поло­жительных зарядах и заканчиваются – на отрицательных.

В отличие от вектора D истоками (стоками) вектора Е могут быть как свободные, так и связанные заряды. Чтобы показать это, перепишем уравнение (1.44) для вектора Е. Подставляя соотношение (1.4) в (1.44), получаем εоdiv Е = ρ – div P. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов , возникающих в результате неравномерной поляризации среды (такие заряды будем называть поляризационными):

divP = -. (1.45)

Поясним возникновение поляризационных зарядов на следующем примере. Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем ΔV, ограниченный поверхностью ΔS. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8 объем ΔVпоказан пунктиром). Подчеркнем, что поляризационные заряды являются «связанными» и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из определения вектора Р (см. 1.2.1).

Рис. 1.8. Поляризованная среда

Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к соотношению εоdiv Е = ρ + ρp, из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды.

Четвертое уравнение Максвелла в интегральной форме сов­падает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора В через любую замкнутую поверхность S равен нулю, т.е.

. (1.46)

Это означает, что не существует линий вектора В, которые только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S): они всегда пронизывают ее (рис. 1.9).

Рис. 1.9. Линии вектора В, пронизывающие поверхность S

Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме урав­нения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим

Уравнение (1.47) представляет собой четвертое уравнение Макс­велла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.

Видео:Уравнения Максвелла 2021Скачать

Третье и четвёртое уравнения Максвелла

Максвелл обобщил теорему Остроградского — Г аусса, выведенную для электростатического поля. Он предположил, что она справедлива для любого как постоянного, так и переменного электрического поля. В формулу теоремы Остроградского — Г аусса

вместо вектора напряжённости Е электрического поля поставим вектор электрической индукции Д (Е = е₀ • е • Д) при е =1, тогда получим

где р — объёмная плотность свободных электрических зарядов.

В правой части третьего уравнения Максвелла интегрирование проводится по объёму V, ограниченному замкнутой поверхностью S.

Согласно третьему уравнению Максвелла, поток вектора электрической индукции D через произвольную замкнутую неподвижную поверхность S определяется величиной

электрического заряда, находящегося внутри этой поверхности, т. е. в объёме V, ограниченном поверхностью S.

Четвёртое уравнение Максвелла выражает, установленный опытным путём, факт отсутствия магнитных зарядов, которые были бы аналогичны электрическим зарядам. Магнитное поле порояедается только электрическими токами.

Четвёртое уравнение Максвелла, записанное в интегральной форме, имеет вид

где В„ — проекция вектора магнитной индукции В на нормаль п к площадке d S.

Поток вектора магнитной индукции (магнитный поток) через произвольную замкнутую неподвижную поверхность S, мысленно проведённую в электромагнитном поле, согласно уравнению (17.95), равен нулю.

Четыре уравнения Максвелла не образуют полной замкнутой системы, позволяющей описать электромагнитное поле при наличии материальной среды. Поэтому необходимо эти уравнения дополнить соотношениями, связывающими векторы Е, Н, D, В и /. Они не являются не зависимыми величинами.

Связь между векторами определяется физическими свойствами среды и её состоянием. Векторы Д и / выражаются через вектор Е, а вектор В — через вектор Н

где Е₀ и ц₀ — соответственно электрическая и магнитная постоянная,

?, ju- диэлектрическая и магнитная проницаемости среды, а — удельная проводимость вещества, из которого состоит среда.

Уравнения (17.96) описывают электромагнитные свойства среды. Для вакуума эти уравнения имеют вид

Система уравнений Максвелла для электромагнитного поля

Запишем полную систему уравнений электромагнитного поля в интегральной форме

Если электрическое поле и магнитное поле — стационарные 3 Г) дв

(— = — = — = о), т. е. не изменяются со временем, то уравнения dt dt dt Максвелла примут вид

Из системы уравнений Максвелла следует, если электрическое поле и магнитное поле стационарные, то они существуют независимо друг от друга. Это позволяет изучать отдельно постоянное электрическое поле и постоянное магнитное поле. Источником электрического поля являются электрические заряды, а источником магнитного поля — электрические токи проводимости.

Если считать, что векторы Е, В, D, Н являются непрерывными функциями координат, то рассматривая циркуляцию векторов НЕ по бесконечно малым контурам и потоки векторов BuD через поверхности, ограничивающие бесконечно малые объёмы, можно от системы интегральных уравнений Максвелла перейти к системе дифференциальных уравнений, описывающей электромагнитное поле в каждой точке пространства. Для этого перехода используют две теоремы векторного анализа — теорему Остроградского-Гаусса и теорему Стокса.

По теореме Остроградского-Гаусса, поток вектора а, через произвольную замкнутую поверхность S, проведённую в электромагнитном поле, равен интегралу от дивергенции вектора а, взятого по объёму V, ограниченного замкнутой поверхностью S

a_x,a_v,a_- проекции вектора а на оси декартовой прямоугольной системы координат.

По теореме Стокса циркуляция вектора а, вдоль произвольного замкнутого контура L, проведённого в электромагнитном поле, равна потоку вектора ротора a (rota) через поверхность S, натянутую на контур L

где вектор rota выражается в декартовых координатах формулой

Запишем полную систему уравнений Максвелла в дифференциальной форме.

Первое уравнение Максвелла

Второе уравнение Максвелла

Третье уравнение Максвелла

Четвёртое уравнение Максвелла

Уравнения, описывающие электрические и магнитные свойства среды имеют вид

Закон Ома, записанный в дифференциальной форме

Система уравнений Максвелла отражает связь электрических и магнитных полей, взаимно порождающих друг друга. Она позволяет по заданной величине электрических зарядов и электрических токов определить характеристики электромагнитного поля, которое они порождают и наоборот.

Уравнения Максвелла лежат в основе электротехники, радиотехники. Они используются в физике плазмы, ядерной физике, астрофизике и др. Уравнения Максвелла не применимы при больших частотах электромагнитных волн, когда велика роль квантовых эффектов. При рассмотрении волновых процессов в главе 21 ещё раз вернёмся к системе уравнений Максвелла.

🎦 Видео

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

3 Уравнения Максвелла в дифференциальной формеСкачать

Вывод уравнений МаксвеллаСкачать

Теория поля 4. Уравнения МаксвеллаСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Билет №34 "Электромагнитные волны"Скачать

Лекция №14 "Электричество и магнетизм" (Попов П.В.): Уравнения МаксвеллаСкачать

6.1 Решение уравнений Максвелла с заданным сторонним электрическим током методом ЭД потенциаловСкачать

Уравнения Максвелла 1Скачать

Физические ошибки. Уравнения МаксвеллаСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать

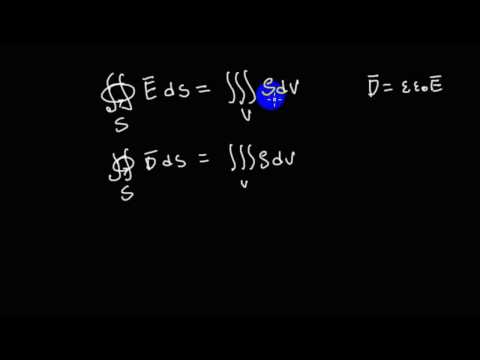
Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

Лекция 233 оператор набла. Уравнения МаксвеллаСкачать

Семинар №7 "Уравнения Максвелла" (Александров Д.А.)Скачать