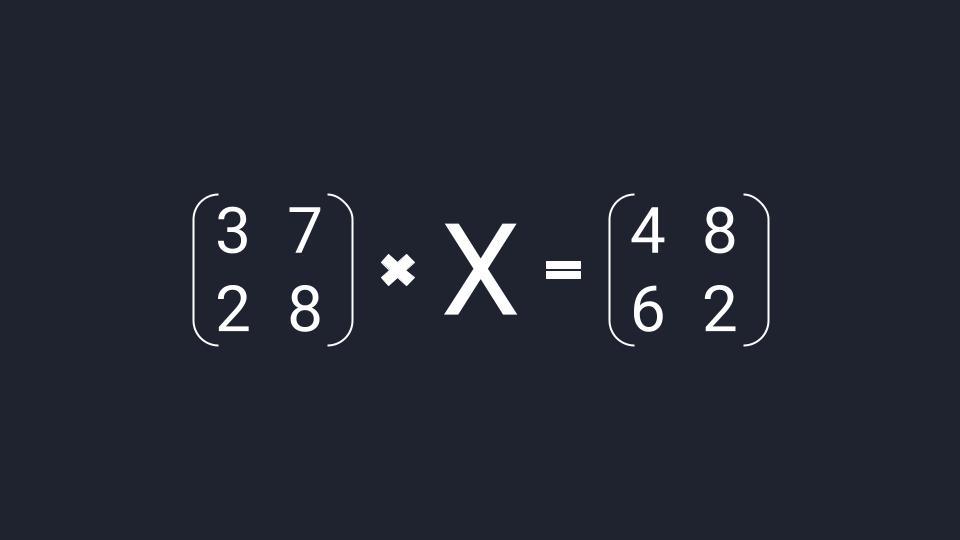- Обратная матрица
- Теорема условия существования обратной матрицы
- Алгоритм нахождения обратной матрицы
- Решение матричных уравнений
- Матричный метод в экономическом анализе
- Решение матричных уравнений: теория и примеры
- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
- 23 решение матричных уравнений ах в ха в ахв с
- Матричные уравнения ах в или ха в
- Матричные уравнения ах в или ха в
- Решение матричных уравнений: теория и примеры
- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
- Решение матричных уравнений
- Что такое матричное уравнение
- Шаг 1. Упрощаем уравнение
- Шаг 2. Вводим единичную матрицу
- Шаг 3. Находим обратную матрицу
- Шаг 4. Вычисляем неизвестную матрицу
- Шаг 5. Проверяем уравнение
- Ну и что
Видео:Лекция 8. Решение матричных уравненийСкачать

Обратная матрица
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2. Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Видео:Решение матричных уравненийСкачать

Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Тогда:
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Решить уравнение АХ = В, если
Решение: Так как обратная матрица равняется (см. пример 1)
Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Матричный метод в экономическом анализе
Наряду с другими экономико-математическими методами в анализе хозяйственной деятельности находят применение также матричные методы. Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2. n), а по вертикальным графам — номера показателей (j = 1,2. m).
На втором этапе по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k. Величина последнего определяется экспертным путем.
Затем определяется рейтинговая оценка по каждой из анализируемых систем по следующей формуле:
На последнем, четвертом этапе найденные величины рейтинговых оценок Rj группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
Видео:Матричное уравнениеСкачать

Решение матричных уравнений: теория и примеры
Видео:Матричный метод решения систем уравненийСкачать

Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:



Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Видео:2 13 Решение матричного уравнения AXB=CСкачать

Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

Видео:§28 Матричные уравненияСкачать

23 решение матричных уравнений ах в ха в ахв с
Чувашский Государственный Университет имени И. Н. Ульянова
Кафедра высшей математики
Курсовая работа на тему:
Решение матричных уравнений
Принял: Доц. Селиверстова Л.В.
Базовые действия над матрицами
Уравнение вида АХ=В
Уравнение вида ХА=В
Уравнение вида АХВ=С
Уравнение вида АХ+ХВ=С
Уравнение вида АХ=ХА
Список использованной литературы
Матричные уравнения — это уравнения, которые в качестве неизвестной содержат матрицу. Матричные уравнения, как и все остальные, бывают разных видов. В данной курсовой работе рассматриваются лишь некоторые виды матричных уравнений, а именно АХ=В, ХА=В, АХВ=С, АХ+ХВ=С, АХ=ХА.
Часто, задачей является не решение матричного уравнения как такового, а системы линейных алгебраических уравнений (сокращенно СЛАУ), которое впоследствии сводится как раз к решению матричного уравнения.
Что касается методов решения матричного уравнении, то их несколько. Простейшие уравнения, такие как АХ=В, ХА=В и АХВ=С, можно решать как с помощью обратной матрицы, так и с помощью элементарных преобразований. Относительно уравнений АХ+ХВ=С и АХ=ХА, то они решаются поэлементно, то есть в качестве неизвестных выступают элементы неизвестной матрицы Х, а не сама матрица.
Перед тем как перейти непосредственно к разбору уравнений. Следует вспомнить базовые действия над матрицами, а также вспомнить понятия обратной матрицы и транспонированной матрицы.
Базовые действия над матрицами
Определение 1 . Две матрица называются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают .
Определение 2. Суммой двух матриц () и () одинаковых порядков называется матрица () того же порядка, элементы которой равны .
На письме это действие может быть записано так: . Операция сложения обладает, очевидно, обычными свойствами: перестановочным ; сочетательным .
Определение 3. Произведением матрицы на число называется матрица , элементы которой равны .
Умножение матрицы на число может быть записано: или .
Эта операция обладает следующими свойствами: сочетательным относительно числового множителя ; распределительным относительно суммы матриц ; распределительным относительно суммы чисел .
После первых двух действий необходимо отметить, что вычитание матриц производится аналогично сложению, а деление матрицы на число может быть определено как умножение на обратное число.
Определение 4. Произведением матрицы (), имеющей порядок , на матрицу (), имеющую порядок , называется матрица (), имеющая порядок , элементы которой равны , где .
Записывается это действие так . Из сказанного выше следует, что для нахождения элемента , в произведении необходимо попарно перемножить все соответствующие элементы -ой строки матрицы на элементы -го столбца матрицы , а затем все это сложить. Из определения также следует, что для умножения двух матриц необходимо, чтобы число столбцов матрицы было равно числу строк матрицы . Отсюда следует, что одновременно произведение и существует только лишь в том случае, когда число столбцов равно числу строк , а число столбцов равно числу строк . В этом случае и будут квадратными матрицами, но разных порядков. Чтобы оба произведения были одинакового порядка, необходимо, чтобы и были квадратными матрицами одинакового порядка.
Произведение матриц имеет свойства:
Перестановочным свойством в общем случае произведение матриц не обладает. Оно выполняется лишь в некоторых случаях.
Среди квадратных матриц необходимо выделить важный класс диагональных матриц.
Определение 5. Диагональной называется квадратная матрица, все элементы которой, расположенные вне главной диагонали, равны 0:
В том случае, если , то для любой квадратной матрицы порядка справедливо . Действительно, для получаем . Для — . Отсюда, .
Среди диагональных матриц с равными друг другу элементами особое место занимают две матрицы: единичная и нулевая. У единичной матрицы , обозначается она — , у нулевой , обозначается она — .
Как было показано , . Перемножив эти матрицы, можно убедиться, что ; .
Таким образом, матрицы и выполняют ту же роль, что и 1 и 0 среди чисел. Вообще нулевой называют любую матрицу, элементы которой равны нулю.
Кроме действий над матрицами как сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу есть также операция делении на матрицу. Она эквивалентна умножению на обратную матрицу. Рассмотрим, что же это такое.
Определение 1. Матрица , удовлетворяющая вместе с матрицей равенствам , где — единичная матрица, называется обратной к и обозначается .
Поскольку и обладают в произведении перестановочным свойством, то обе матрицы должны быть квадратными и одного порядка.
Прежде чем рассматривать вопрос о существовании обратной матрицы, введем некоторые понятия.
Определение 2. Если определитель квадратной матрицы отличен от нуля, то матрица называется невырожденной. В противном случае она называется вырожденной.
Определение 3. Пусть дана квадратная матрица
Матрицей союзной или присоединенной к матрице называется матрица
где алгебраические дополнения элементов данной матрицы.
Необходимо обратить внимание на то, что в матрице алгебраические дополнения к элементам -ой строки расположены в -ом столбце.
Теорема 1. Определитель произведения матриц равен произведению определителей этих матриц, то есть .
Теорема 2. Матрица имеет обратную только в том случае, если она невырожденная.
Доказательство. Пусть для матрицы существует обратная , тогда . Отсюда следует, что
иначе единицы справа быть не может.
Теорема 3. У каждой невырожденной матрицы существует единственная обратная .
Доказательство. Пусть имеет две обратные матрицы и . Тогда
Теорема 4. У каждой невырожденной квадратной матрицы существует обратная, равная .
Докажем эту теорему, вычисляя . Очевидно, что мы должны получить при этом матрицу , элементы которой находятся по формуле
В полученном выражении, если , то . Действительно,
похоже на выражение для вычисления величины определителя. При этом элементы -ой строки умножаются на алгебраические дополнения -го столбца. Но так как эти дополнения содержат в себе -ую строку, то получается, что мы вычисляем определитель с двумя одинаковыми строками. Значит, он равен нулю.
Итак, если , то . Если же , то полученное выражение в точности соответствует формуле для вычисления определителя. Значит,
Но определяет диагональные элементы. Значит, в полученной матрице по главной диагонали стоят единицы, а остальные элементы — нули. Это единичная матрица . Следовательно,
Отсюда следует правило вычисления обратной матрицы:
. находим (он должен быть не равен нулю)
. заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением
. делим каждый полученный элемент на .
Обратную матрицу матрицы 2х2 удобно находить по формуле:
Определение 1. Уравнение, называется матричным, если в качестве неизвестного оно содержит матрицу.
Определение 2. Простейшими матричными уравнениями называются равенства вида
AX=B, XA=B, AXA=B, AX=XB, AX+XB=C
где A,B,C — данные матрицы, X — матрица, которую необходимо найти.
Определение 3. Некоторую матрицу называют решением матричного уравнения, если при её подстановке вместо матричное уравнение превращается в тождество.
матричное уравнение решение
Уравнения вида АХ=В
Рассмотрим уравнение вида AX=B, где A,B — известные матрицы, причём матрица A квадратная и невырожденная, а матрица B имеет тоже количество строк, что и матрица A.
Такое уравнение можно решить двумя способами:
. Вычисляется обратная матрица любым из известных способов. Тогда решение матричного уравнения будет иметь вид:
2. При помощи элементарных преобразований строк блочной матрицы (A|B) к виду , где E — единичная матрица. Тогда матрица будет решением уравнения.
Найдём решение матричного уравнения АХ=В, имеющего вид
. Найдём матрицу, обратную матрице А по правилу нахождения обратной матрицы 2-го порядка:
. Запишем матрицу (A|B) и выполним элементарные преобразования, чтобы получить слева единичную матрицу:
В обоих случаях получили
Уравнение вида ХА=В
Матричное уравнение ХА=В также можно решить двумя способами:
. Вычисляется обратная матрица любым из известных способов. Тогда решение матричного уравнения будет иметь вид:
. Транспонированием левой и правой частей уравнения получим
После введения новой неизвестной матрицы получаем уравнение вида
которое можно решить методом элементарных преобразований, составив блочную матрицу .
Найдём решение матричного уравнения ХА=В, имеющего вид
. Так как обратная матрица была найдена нами в предыдущем примере, то находим
2. Транспонируем обе части уравнения
Составим блочную матрицу и при помощи элементарных преобразований получим слева единичную
что совпадает с решением, полученным первым способом.
Уравнения вида АХВ=С
При решении этого уравнения необходимо обе части уравнения умножить на слева и на справа. Учитывая, что
мы получаем, что указанное уравнение решается по формуле
Решить уравнение вида АХВ=С, где
Уравнение принимает вид
Найдем матрицу по формуле
Далее, применяя формулу получаем:
Уравнение вида АХ+ХВ=С
Для решения уравнений вида АХ=ХВ, АХ+ХВ=С описанные выше методы не подходят. Они не подходят также для решения уравнений, в которых хотя бы один из сомножителей при неизвестной матрице Х является вырожденной матрицей.
В таких случаях матрицу Х выписывают поэлементно (т.е. неизвестными будут элементы матрицы Х, а не матрица в целом), проводят указанные в уравнении действия над матрицами и равенство двух частей уравнения записывают поэлементно. В результате получают систему линейных уравнений, решив которую, находят возможные значения элементов матрицы Х. Если система оказывается несовместной, то исходное матричное уравнение не имеет решений.
Решить матричное уравнение АХ+ХВ=С, где
Запишем матрицу Х поэлементно:
Тогда в подробной записи матричное уравнение примет вид:
Вычислив произведения в левой части уравнения и сложив эти произведения, придем к уравнению
Записывая это матричное уравнение по элементам, получим систему уравнений:
Решив эту систему, найдем х=2, у=3, z=3, v=4.
Следовательно, искомая матрица имеет вид:
Уравнение вида АХ=ХА
Уравнения вида АХ=ХА решаются так же, как и в предыдущем случае, то есть поэлементно. Решение здесь сводится к нахождению перестановочной матрицы. Подробнее рассмотрим на примере.
Найдите все матрицы, перестановочные с данной матрицей А:
Наша цель — найти все матрицы В такие, что
Для того, чтобы существовала левая часть этого равенства нужно, чтобы длина строки матрицы В равнялась двум. Для существования правой части равенства надо, чтобы высота столбца матрицы В равнялась двум. Итак, матрица В должна быть квадратной матрицей второго порядка:
Теперь условие задачи запишется в виде равенства:
Но равенство матриц означает равенство их элементов, занимающих одинаковые места. Значит
Эти равенства дают нам систему четырех уравнений с четырьмя неизвестными:
Получили общее решение системы линейных уравнений. Значит, общий вид матрицы В будет таков:
где х2 и х4 — любые действительные числа.
где х2 и х4 — любые действительные числа.
1. Ф.Р. Гантмахер «Теория матриц».
. Х.Д. Икрамов «Численное решение матричных уравнений».
. Курс лекций Б.М. Верникова, А.Я. Овсянникова.
. Высшая математика (Учеб. пособие). Никулина Л.С., Степанова А.А.
Теги: Решение матричных уравнений Курсовая работа (теория) Математика
Видео:§29 Решение матричного уравненияСкачать

Матричные уравнения ах в или ха в
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Матричные уравнения ах в или ха в
Чувашский Государственный Университет имени И. Н. Ульянова
Кафедра высшей математики
Курсовая работа на тему:
Решение матричных уравнений
Принял: Доц. Селиверстова Л.В.
Базовые действия над матрицами
Уравнение вида АХ=В
Уравнение вида ХА=В
Уравнение вида АХВ=С
Уравнение вида АХ+ХВ=С
Уравнение вида АХ=ХА
Список использованной литературы
Матричные уравнения — это уравнения, которые в качестве неизвестной содержат матрицу. Матричные уравнения, как и все остальные, бывают разных видов. В данной курсовой работе рассматриваются лишь некоторые виды матричных уравнений, а именно АХ=В, ХА=В, АХВ=С, АХ+ХВ=С, АХ=ХА.
Часто, задачей является не решение матричного уравнения как такового, а системы линейных алгебраических уравнений (сокращенно СЛАУ), которое впоследствии сводится как раз к решению матричного уравнения.
Что касается методов решения матричного уравнении, то их несколько. Простейшие уравнения, такие как АХ=В, ХА=В и АХВ=С, можно решать как с помощью обратной матрицы, так и с помощью элементарных преобразований. Относительно уравнений АХ+ХВ=С и АХ=ХА, то они решаются поэлементно, то есть в качестве неизвестных выступают элементы неизвестной матрицы Х, а не сама матрица.
Перед тем как перейти непосредственно к разбору уравнений. Следует вспомнить базовые действия над матрицами, а также вспомнить понятия обратной матрицы и транспонированной матрицы.
Базовые действия над матрицами
Определение 1 . Две матрица называются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают .
Определение 2. Суммой двух матриц () и () одинаковых порядков называется матрица () того же порядка, элементы которой равны .
На письме это действие может быть записано так: . Операция сложения обладает, очевидно, обычными свойствами: перестановочным ; сочетательным .
Определение 3. Произведением матрицы на число называется матрица , элементы которой равны .
Умножение матрицы на число может быть записано: или .
Эта операция обладает следующими свойствами: сочетательным относительно числового множителя ; распределительным относительно суммы матриц ; распределительным относительно суммы чисел .
После первых двух действий необходимо отметить, что вычитание матриц производится аналогично сложению, а деление матрицы на число может быть определено как умножение на обратное число.
Определение 4. Произведением матрицы (), имеющей порядок , на матрицу (), имеющую порядок , называется матрица (), имеющая порядок , элементы которой равны , где .
Записывается это действие так . Из сказанного выше следует, что для нахождения элемента , в произведении необходимо попарно перемножить все соответствующие элементы -ой строки матрицы на элементы -го столбца матрицы , а затем все это сложить. Из определения также следует, что для умножения двух матриц необходимо, чтобы число столбцов матрицы было равно числу строк матрицы . Отсюда следует, что одновременно произведение и существует только лишь в том случае, когда число столбцов равно числу строк , а число столбцов равно числу строк . В этом случае и будут квадратными матрицами, но разных порядков. Чтобы оба произведения были одинакового порядка, необходимо, чтобы и были квадратными матрицами одинакового порядка.
Произведение матриц имеет свойства:
Перестановочным свойством в общем случае произведение матриц не обладает. Оно выполняется лишь в некоторых случаях.
Среди квадратных матриц необходимо выделить важный класс диагональных матриц.
Определение 5. Диагональной называется квадратная матрица, все элементы которой, расположенные вне главной диагонали, равны 0:
В том случае, если , то для любой квадратной матрицы порядка справедливо . Действительно, для получаем . Для — . Отсюда, .
Среди диагональных матриц с равными друг другу элементами особое место занимают две матрицы: единичная и нулевая. У единичной матрицы , обозначается она — , у нулевой , обозначается она — .
Как было показано , . Перемножив эти матрицы, можно убедиться, что ; .
Таким образом, матрицы и выполняют ту же роль, что и 1 и 0 среди чисел. Вообще нулевой называют любую матрицу, элементы которой равны нулю.
Кроме действий над матрицами как сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу есть также операция делении на матрицу. Она эквивалентна умножению на обратную матрицу. Рассмотрим, что же это такое.
Определение 1. Матрица , удовлетворяющая вместе с матрицей равенствам , где — единичная матрица, называется обратной к и обозначается .
Поскольку и обладают в произведении перестановочным свойством, то обе матрицы должны быть квадратными и одного порядка.
Прежде чем рассматривать вопрос о существовании обратной матрицы, введем некоторые понятия.
Определение 2. Если определитель квадратной матрицы отличен от нуля, то матрица называется невырожденной. В противном случае она называется вырожденной.
Определение 3. Пусть дана квадратная матрица
Матрицей союзной или присоединенной к матрице называется матрица
где алгебраические дополнения элементов данной матрицы.
Необходимо обратить внимание на то, что в матрице алгебраические дополнения к элементам -ой строки расположены в -ом столбце.
Теорема 1. Определитель произведения матриц равен произведению определителей этих матриц, то есть .
Теорема 2. Матрица имеет обратную только в том случае, если она невырожденная.
Доказательство. Пусть для матрицы существует обратная , тогда . Отсюда следует, что
иначе единицы справа быть не может.
Теорема 3. У каждой невырожденной матрицы существует единственная обратная .
Доказательство. Пусть имеет две обратные матрицы и . Тогда
Теорема 4. У каждой невырожденной квадратной матрицы существует обратная, равная .
Докажем эту теорему, вычисляя . Очевидно, что мы должны получить при этом матрицу , элементы которой находятся по формуле
В полученном выражении, если , то . Действительно,
похоже на выражение для вычисления величины определителя. При этом элементы -ой строки умножаются на алгебраические дополнения -го столбца. Но так как эти дополнения содержат в себе -ую строку, то получается, что мы вычисляем определитель с двумя одинаковыми строками. Значит, он равен нулю.
Итак, если , то . Если же , то полученное выражение в точности соответствует формуле для вычисления определителя. Значит,
Но определяет диагональные элементы. Значит, в полученной матрице по главной диагонали стоят единицы, а остальные элементы — нули. Это единичная матрица . Следовательно,
Отсюда следует правило вычисления обратной матрицы:
. находим (он должен быть не равен нулю)
. заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением
. делим каждый полученный элемент на .
Обратную матрицу матрицы 2х2 удобно находить по формуле:
Определение 1. Уравнение, называется матричным, если в качестве неизвестного оно содержит матрицу.
Определение 2. Простейшими матричными уравнениями называются равенства вида
AX=B, XA=B, AXA=B, AX=XB, AX+XB=C
где A,B,C — данные матрицы, X — матрица, которую необходимо найти.
Определение 3. Некоторую матрицу называют решением матричного уравнения, если при её подстановке вместо матричное уравнение превращается в тождество.
матричное уравнение решение
Уравнения вида АХ=В
Рассмотрим уравнение вида AX=B, где A,B — известные матрицы, причём матрица A квадратная и невырожденная, а матрица B имеет тоже количество строк, что и матрица A.
Такое уравнение можно решить двумя способами:
. Вычисляется обратная матрица любым из известных способов. Тогда решение матричного уравнения будет иметь вид:
2. При помощи элементарных преобразований строк блочной матрицы (A|B) к виду , где E — единичная матрица. Тогда матрица будет решением уравнения.
Найдём решение матричного уравнения АХ=В, имеющего вид
. Найдём матрицу, обратную матрице А по правилу нахождения обратной матрицы 2-го порядка:
. Запишем матрицу (A|B) и выполним элементарные преобразования, чтобы получить слева единичную матрицу:
В обоих случаях получили
Уравнение вида ХА=В
Матричное уравнение ХА=В также можно решить двумя способами:
. Вычисляется обратная матрица любым из известных способов. Тогда решение матричного уравнения будет иметь вид:
. Транспонированием левой и правой частей уравнения получим
После введения новой неизвестной матрицы получаем уравнение вида
которое можно решить методом элементарных преобразований, составив блочную матрицу .
Найдём решение матричного уравнения ХА=В, имеющего вид
. Так как обратная матрица была найдена нами в предыдущем примере, то находим
2. Транспонируем обе части уравнения
Составим блочную матрицу и при помощи элементарных преобразований получим слева единичную
что совпадает с решением, полученным первым способом.
Уравнения вида АХВ=С
При решении этого уравнения необходимо обе части уравнения умножить на слева и на справа. Учитывая, что
мы получаем, что указанное уравнение решается по формуле
Решить уравнение вида АХВ=С, где
Уравнение принимает вид
Найдем матрицу по формуле
Далее, применяя формулу получаем:
Уравнение вида АХ+ХВ=С
Для решения уравнений вида АХ=ХВ, АХ+ХВ=С описанные выше методы не подходят. Они не подходят также для решения уравнений, в которых хотя бы один из сомножителей при неизвестной матрице Х является вырожденной матрицей.
В таких случаях матрицу Х выписывают поэлементно (т.е. неизвестными будут элементы матрицы Х, а не матрица в целом), проводят указанные в уравнении действия над матрицами и равенство двух частей уравнения записывают поэлементно. В результате получают систему линейных уравнений, решив которую, находят возможные значения элементов матрицы Х. Если система оказывается несовместной, то исходное матричное уравнение не имеет решений.
Решить матричное уравнение АХ+ХВ=С, где
Запишем матрицу Х поэлементно:
Тогда в подробной записи матричное уравнение примет вид:
Вычислив произведения в левой части уравнения и сложив эти произведения, придем к уравнению
Записывая это матричное уравнение по элементам, получим систему уравнений:
Решив эту систему, найдем х=2, у=3, z=3, v=4.
Следовательно, искомая матрица имеет вид:
Уравнение вида АХ=ХА
Уравнения вида АХ=ХА решаются так же, как и в предыдущем случае, то есть поэлементно. Решение здесь сводится к нахождению перестановочной матрицы. Подробнее рассмотрим на примере.
Найдите все матрицы, перестановочные с данной матрицей А:
Наша цель — найти все матрицы В такие, что
Для того, чтобы существовала левая часть этого равенства нужно, чтобы длина строки матрицы В равнялась двум. Для существования правой части равенства надо, чтобы высота столбца матрицы В равнялась двум. Итак, матрица В должна быть квадратной матрицей второго порядка:
Теперь условие задачи запишется в виде равенства:
Но равенство матриц означает равенство их элементов, занимающих одинаковые места. Значит
Эти равенства дают нам систему четырех уравнений с четырьмя неизвестными:
Получили общее решение системы линейных уравнений. Значит, общий вид матрицы В будет таков:
где х2 и х4 — любые действительные числа.
где х2 и х4 — любые действительные числа.
1. Ф.Р. Гантмахер «Теория матриц».
. Х.Д. Икрамов «Численное решение матричных уравнений».
. Курс лекций Б.М. Верникова, А.Я. Овсянникова.
. Высшая математика (Учеб. пособие). Никулина Л.С., Степанова А.А.
Теги: Решение матричных уравнений Курсовая работа (теория) Математика
Видео:Решение матричного уравнения X(6 8; 2 1) = (4 −3; 1 6) Высшая математика. Матрицы.Скачать

Решение матричных уравнений: теория и примеры
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:



Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

Видео:Обратная матрица. Решение матричных уравненийСкачать

Решение матричных уравнений
Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Видео:Решение матричных уравненийСкачать

Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Видео:Решение матричного уравнения (1 3; 1 2)X = (2 −2 6; 1 3 4) Высшая математика. Матрицы.Скачать

Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
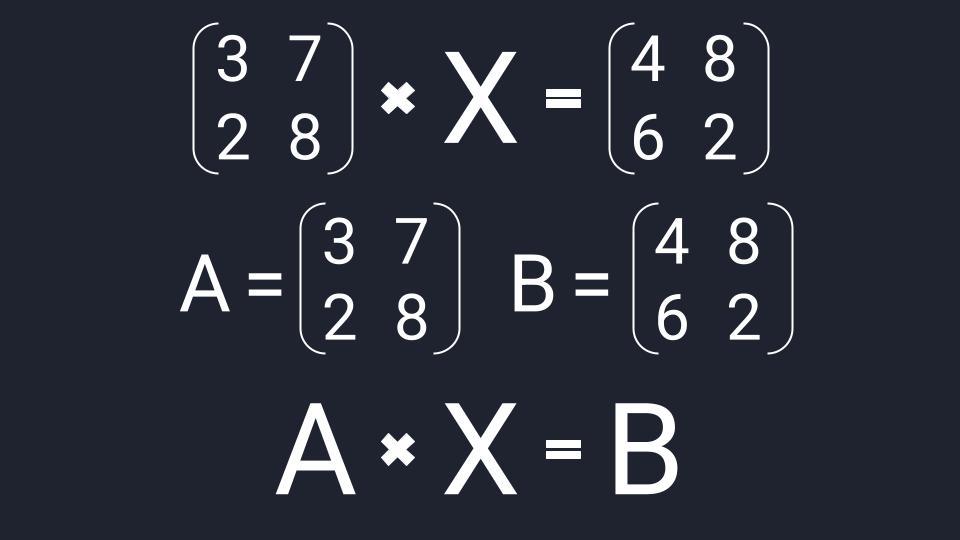
Видео:Решение матричного уравнения (−1 1; 2 −3)X = (−2 3; 1 −4)Скачать

Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Видео:Решение системы уравнений методом ГауссаСкачать

Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Видео:Матричные уравненияСкачать

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Видео:Решение матричного уравнения (−3 2; 5 −3)X = (−2 4; 3 −1) Высшая математика. Матрицы.Скачать

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика: