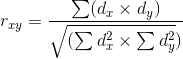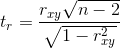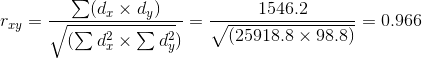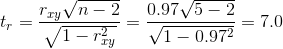- Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
- Критерии и методы
- КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
- 1. История разработки критерия корреляции
- 2. Для чего используется критерий корреляции Пирсона?
- 3. Условия и ограничения применения критерия хи-квадрат Пирсона
- 4. Как рассчитать коэффициента корреляции Пирсона?
- 5. Как интерпретировать значение коэффициента корреляции Пирсона?
- 6. Пример расчета коэффициента корреляции Пирсона
- 7.1 Дисперсионный анализ
- 7.1.1 Однофакторный дисперсионный анализ для несвязанных выборок
- 7.1.2 Дисперсионный анализ для связанных выборок
- 7.2 Корреляционный анализ
- 7.2.1 Понятие корреляционной связи
- Применение корреляционного анализа в психологии 4117
- 🎥 Видео
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Видео:Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Критерии и методы
Видео:КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12Скачать

КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
- Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой — определяются при помощи регрессионного анализа.
- Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
- Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
- Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Значения коэффициента корреляции Пирсона интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение rxy – тем выше теснота связи между двумя величинами. rxy = 0 говорит о полном отсутствии связи. rxy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка.
Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy 0.7 — о сильной связи.
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) |
| 1. | 951 | 83 |
| 2. | 874 | 76 |
| 3. | 957 | 84 |
| 4. | 1084 | 89 |
| 5. | 903 | 79 |
- Вычислим суммы анализируемых значений X и Y:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Найдем средние арифметические для X и Y:
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) |
| 1. | 951 | 83 | -2.8 | 0.8 |
| 2. | 874 | 76 | -79.8 | -6.2 |
| 3. | 957 | 84 | 3.2 | 1.8 |
| 4. | 1084 | 89 | 130.2 | 6.8 |
| 5. | 903 | 79 | -50.8 | -3.2 |
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) | dx 2 | dy 2 |
| 1. | 951 | 83 | -2.8 | 0.8 | 7.84 | 0.64 |
| 2. | 874 | 76 | -79.8 | -6.2 | 6368.04 | 38.44 |
| 3. | 957 | 84 | 3.2 | 1.8 | 10.24 | 3.24 |
| 4. | 1084 | 89 | 130.2 | 6.8 | 16952,04 | 46.24 |
| 5. | 903 | 79 | -50.8 | -3.2 | 2580,64 | 10.24 |
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) | dx 2 | dy 2 | dx x dy |
| 1. | 951 | 83 | -2.8 | 0.8 | 7.84 | 0.64 | -2.24 |
| 2. | 874 | 76 | -79.8 | -6.2 | 6368.04 | 38.44 | 494.76 |
| 3. | 957 | 84 | 3.2 | 1.8 | 10.24 | 3.24 | 5.76 |
| 4. | 1084 | 89 | 130.2 | 6.8 | 16952,04 | 46.24 | 885.36 |
| 5. | 903 | 79 | -50.8 | -3.2 | 2580,64 | 10.24 | 162.56 |
Найдем значение суммы произведений отклонений Σ(dx x dy):
Рассчитаем значение коэффициента корреляции Пирсона rxy по приведенной выше формуле:
Найдем значение t-критерия для оценки статистической значимости корреляционной связи:
Критическое значение t-критерия найдем по таблице, где при числе степеней свободы f = n-2 = 3 и уровне значимости p = 0.01 значение tкрит = 5.84. Рассчитанное значение tr (7.0) больше tкрит (5.84), следовательно связь является статистически значимой.
Сделаем статистический вывод:
Видео:Корреляционный анализ Спирмена. Коэффициент корреляции Спирмена. КОРРЕЛЯЦИЯ. АНАЛИЗ ДАННЫХ.Скачать

7.1 Дисперсионный анализ
Дисперсионный анализ, предложенный Р. Фишером, является статистическим методом, предназначенным для выявления влияния ряда отдельных факторов на результаты экспериментов.
В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные), а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.
Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F — критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.
Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).
Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным. (Суходольский Г.В., 1972; Шеффе Г., 1980).
Видео:Математика #1 | Корреляция и регрессияСкачать

7.1.1 Однофакторный дисперсионный анализ для несвязанных выборок
Изучается действие только одной переменной (фактора) на исследуемый признак. Исследователя интересует вопрос, как изменяется определенный признак в разных условиях действия переменной (фактора). Например, как изменяется время решения задачи при разных условиях мотивации испытуемых (низкой, средней, высокой мотивации) или при разных способах предъявления задачи (устно, письменно или в виде текста с графиками и иллюстрациями), в разных условиях работы с задачей (в одиночестве, в комнате с преподавателем, в классе). В первом случае фактором является мотивация, во втором – степень наглядности, в третьем – фактор публичности. [1]
В данном варианте метода влиянию каждой из градаций подвергаются разные выборки испытуемых. Градаций фактора должно быть не менее трех.
Пример 1. Три различные группы из шести испытуемых получили списки из десяти слов. Первой группе слова предъявлялись с низкой скоростью -1 слово в 5 секунд, второй группе со средней скоростью — 1 слово в 2 секунды, и третьей группе с большой скоростью — 1 слово в секунду. Было предсказано, что показатели воспроизведения будут зависеть от скорости предъявления слов. Результаты представлены в табл. 1.
Таблица 1. Количество воспроизведенных слов (по J . Greene , M D ‘ Olivera , 1989, p . 99)
Группа 1 низкая скорость
Группа 2 средняя скорость
Группа 3 высокая скорость
Дисперсионный однофакторный анализ позволяет проверить гипотезы:
H 0 : различия в объеме воспроизведения слов между группами являются не более выраженными, чем случайные различия внутри каждой группы
H 1 : Различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы.
Последовательность операций в однофакторном дисперсионном анализе для несвязанных выборок:
1. подсчитаем SS факт — вариативность признака, обусловленную действием исследуемого фактора. Часто встречающееся обозначение SS — сокращение от «суммы квадратов» ( sum of squares ). Это сокращение чаще всего используется в переводных источниках (см., например: Гласс Дж., Стенли Дж., 1976).

где Тс – сумма индивидуальных значений по каждому из условий. Для нашего примера 43, 37, 24 (см. табл. 1);
с – количество условий (градаций) фактора (=3);
n – количество испытуемых в каждой группе (=6);
N – общее количество индивидуальных значений (=18);

Отметим разницу между 

По формуле (1) рассчитав фактическую вариативность признака, получаем:
2. подсчитаем SS общ – общую вариативность признака:

3. подсчитаем случайную (остаточную) величину SS сл , обусловленную неучтенными факторами:

4. число степеней свободы равно:


5. «средний квадрат» или математическое ожидание суммы квадратов, усредненная величина соответствующих сумм квадратов SS равна:

6. значение статистики критерия F эмп рассчитаем по формуле:

Для нашего примера имеем: F эмп=15,72/2,11=7,45
7. определим F крит по статистическим таблицам Приложения 3 для df 1= k 1=2 и df 2= k 2=15 табличное значение статистики равно 3,68
8. если F эмп F крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная гипотеза. Для нашего примера F эмп > F крит (7.45>3.68), следовательно п ринимается альтернативная гипотеза.
Вывод: различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы (р
Видео:Ранговая корреляция СпирменаСкачать

7.1.2 Дисперсионный анализ для связанных выборок
Метод дисперсионного анализа для связанных выборок применяется в тех случаях, когда исследуется влияние разных градаций фактора или разных условий на одну и ту же выборку испытуемых. Градаций фактора должно быть не менее трех.
В данном случае различия между испытуемыми — возможный самостоятельный источник различий. Однофакторный дисперсионный анализ для связанных выборок позволит определить, что перевешивает — тенденция, выраженная кривой изменения фактора, или индивидуальные различия между испытуемыми. Фактор индивидуальных различий может оказаться более значимым, чем фактор изменения экспериментальных условий.
Пример 2. Группа из 5 испытуемых была обследована с помощью трех экспериментальных заданий, направленных на изучение интеллектуальной, настойчивости (Сидоренко Е. В., 1984). Каждому испытуемому индивидуально предъявлялись последовательно три одинаковые анаграммы: четырехбуквенная, пятибуквенная и шестибуквенная. Можно ли считать, что фактор длины анаграммы влияет на длительность попыток ее решения?
Таблица 2. Длительность решения анаграмм (сек)
Условие 1. четырехбуквенная анаграмма
Условие 2. Пятибуквенная анаграмма
Условие 3. шестибуквенная анаграмма
Суммы по испытуемым
Сформулируем гипотезы. Наборов гипотез в данном случае два.
Н0(А): Различия в длительности попыток решения анаграмм разной длины являются не более выраженными, чем различия, обусловленные случайными причинами.
Н1(А): Различия в длительности попыток решения анаграмм разной длины являются более выраженными, чем различия, обусловленные случайными причинами.
Но(Б): Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.
Н1(Б): Индивидуальные различия между испытуемыми являются более выраженными, чем различия, обусловленные случайными причинами.
Последовательность операций в однофакторном дисперсионном анализе для связанных выборок:
1. подсчитаем SS факт — вариативность признака, обусловленную действием исследуемого фактора по формуле (1).

где Тс – сумма индивидуальных значений по каждому из условий (столбцов). Для нашего примера 51, 1244, 47 (см. табл. 2); с – количество условий (градаций) фактора (=3); n – количество испытуемых в каждой группе (=5); N – общее количество индивидуальных значений (=15); 
2. подсчитаем SS исп — вариативность признака, обусловленную индивидуальными значения испытуемых.
где Ти – сумма индивидуальных значений по каждому испытуемому. Для нашего примера 247, 631, 100, 181, 183 (см. табл. 2); с – количество условий (градаций) фактора (=3); N – общее количество индивидуальных значений (=15);
3. подсчитаем SS общ – общую вариативность признака по формуле (2):
4. подсчитаем случайную (остаточную) величину SS сл , обусловленную неучтенными факторами по формуле (3):
5. число степеней свободы равно (4):



6. «средний квадрат» или математическое ожидание суммы квадратов, усредненная величина соответствующих сумм квадратов SS равна (5):

7. значение статистики критерия F эмп рассчитаем по формуле (6 ):

8. определим F крит по статистическим таблицам Приложения 3 для df 1= k 1=2 и df 2= k 2=8 табличное значение статистики F крит_факт=4,46, и для df 3= k 3=4 и df 2= k 2=8 F крит_исп=3,84
9. F эмп_факт > F крит_факт (6,872>4,46), следовательно п ринимается альтернативная гипотеза.
10. F эмп_исп F крит_исп (1,054 ринимается нулевая гипотеза.
Вывод: различия в объеме воспроизведения слов в разных условиях являются более выраженными, чем различия, обусловленные случайными причинами (р Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.
Видео:Коэффициент корреляции Пирсона в ExcelСкачать

7.2 Корреляционный анализ
Видео:Коэффициент корреляции ПирсонаСкачать

7.2.1 Понятие корреляционной связи
Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или связана ли продолжительность работы учителя в школе с размером его заработной платы, или с чем больше связан уровень умственного развития учащихся — с их успеваемостью по математике или по литературе и т.п.?
Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.
Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем больше рост, тем больше вес человека. Однако из этого правила имеются исключения, когда относительно низкие люди имеют избыточный вес, и, наоборот, астеники, при высоком росте имеют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д.
Корреляционные связи — это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. «Оба термина, — пишет Е.В. Сидоренко, — корреляционная связь и корреляционная зависимость — часто используются как синонимы. Зависимость подразумевает влияние, связь — любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.
Корреляционная зависимость — это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака (Е.В. Сидоренко, 2000).
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Корреляционные связи различаются по форме, направлению и степени (силе).

Рис.1. Связь между эффективностью решения задачи
и силой мотивационной тенденции (по J. W. A t k in son, 1974, р 200)
По направлению корреляционная связь может быть положительной («прямой») и отрицательной («обратной»). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака — низкие значения другого. При отрицательной корреляции соотношения обратные. При положительной корреляции коэффициент корреляции имеет положительный знак, например r =+0,207 , при отрицательной корреляции — отрицательный знак, например r =—0,207 .
Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.
Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Максимальное возможное абсолютное значение коэффициента корреляции r =1,00 ; минимальное r =0,00 .
Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):
сильная , или тесная при коэффициенте корреляции r >0,70 ;
очень слабая при r Y могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции (см. табл. 3):
Таблица 3. Использование коэффициента корреляции в зависимости от типа переменных
Видео:Корреляционный анализСкачать

Применение корреляционного анализа в психологии 4117
Шишлянникова Л.М.
заведующая учебно-производственной лабораторией математических моделей в психологии и педагогике, ФГБОУ ВО МГППУ, Москва, Россия
e-mail: Sh-lyubov@yandex.ru
Ссылка для цитирования
Применение статистических методов при обработке материалов психологических исследований дает большую возможность извлечь из экспериментальных данных полезную информацию. Одним из самых распространенных методов статистики является корреляционный анализ.
Термин «корреляция» впервые применил французский палеонтолог Ж. Кювье, который вывел «закон корреляции частей и органов животных» (этот закон позволяет восстанавливать по найденным частям тела облик всего животного). В статистику указанный термин ввел английский биолог и статистик Ф. Гальтон (не просто «связь» – relation , а «как бы связь» – corelation ).
Корреляционный анализ – это проверка гипотез о связях между переменными с использованием коэффициентов корреляции, двумерной описательной статистики, количественной меры взаимосвязи (совместной изменчивости) двух переменных. Таким образом, это совокупность методов обнаружения корреляционной зависимости между случайными величинами или признаками.
Корреляционный анализ для двух случайных величин заключает в себе:
- построение корреляционного поля и составление корреляционной таблицы;
- вычисление выборочных коэффициентов корреляции и корреляционных отношений;
- проверку статистической гипотезы значимости связи.
Основное назначение корреляционного анализа – выявление связи между двумя или более изучаемыми переменными, которая рассматривается как совместное согласованное изменение двух исследуемых характеристик. Данная изменчивость обладает тремя основными характериcтиками: формой, направлением и силой.
По форме корреляционная связь может быть линейной или нелинейной. Более удобной для выявления и интерпретации корреляционной связи является линейная форма. Для линейной корреляционной связи можно выделить два основных направления: положительное («прямая связь») и отрицательное («обратная связь»).
Сила связи напрямую указывает, насколько ярко проявляется совместная изменчивость изучаемых переменных. В психологии функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания – график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку.
В качестве числовой характеристики вероятностной связи используют коэффициенты корреляции, значения которых изменяются в диапазоне от –1 до +1. После проведения расчетов исследователь, как правило, отбирает только наиболее сильные корреляции, которые в дальнейшем интерпретируются (табл. 1).
Критерием для отбора «достаточно сильных» корреляций может быть как абсолютное значение самого коэффициента корреляции (от 0,7 до 1), так и относительная величина этого коэффициента, определяемая по уровню статистической значимости (от 0,01 до 0,1), зависящему от размера выборки. В малых выборках для дальнейшей интерпретации корректнее отбирать сильные корреляции на основании уровня статистической значимости. Для исследований, которые проведены на больших выборках, лучше использовать абсолютные значения коэффициентов корреляции.
Таким образом, задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
В настоящее время разработано множество различных коэффициентов корреляции. Наиболее применяемыми являются r -Пирсона, r -Спирмена и τ -Кендалла. Современные компьютерные статистические программы в меню «Корреляции» предлагают именно эти три коэффициента, а для решения других исследовательских задач предлагаются методы сравнения групп.
Выбор метода вычисления коэффициента корреляции зависит от типа шкалы, к которой относятся переменные (табл. 2).
Для переменных с интервальной и с номинальной шкалой используется коэффициент корреляции Пирсона (корреляция моментов произведений). Если, по меньшей мере, одна из двух переменных имеет порядковую шкалу или не является нормально распределенной, используется ранговая корреляция по Спирмену или
t-Кендалла. Если же одна из двух переменных является дихотомической, можно использовать точечную двухрядную корреляцию (в статистической компьютерной программе SPSS эта возможность отсутствует, вместо нее может быть применен расчет ранговой корреляции). В том случае если обе переменные являются дихотомическими, используется четырехполевая корреляция (данный вид корреляции рассчитываются SPSS на основании определения мер расстояния и мер сходства). Расчет коэффициента корреляции между двумя недихотомическими переменными возможен только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U -образная (неоднозначная), коэффициент корреляции не пригоден для использования в качестве меры силы связи: его значение стремится к нулю.
Таким образом, условия применения коэффициентов корреляции будут следующими:
- переменные, измеренные в количественной (ранговой, метрической) шкале на одной и той же выборке объектов;
- связь между переменными является монотонной.
Основная статистическая гипотеза, которая проверяется корреляционным анализом, является ненаправленной и содержит утверждение о равенстве корреляции нулю в генеральной совокупности H 0 : r xy = 0. При ее отклонении принимается альтернативная гипотеза H 1 : r xy ≠ 0 о наличии положительной или отрицательной корреляции – в зависимости от знака вычисленного коэффициента корреляции.
На основании принятия или отклонения гипотез делаются содержательные выводы. Если по результатам статистической проверки H 0 : r xy = 0 не отклоняется на уровне a, то содержательный вывод будет следующим: связь между X и Y не обнаружена. Если же при H 0 r xy = 0 отклоняется на уровне a, значит, обнаружена положительная (отрицательная) связь между X и Y . Однако к интерпретации выявленных корреляционных связей следует подходить осторожно. С научной точки зрения, простое установление связи между двумя переменными не означает существования причинно-следственных отношений. Более того, наличие корреляции не устанавливает отношения последовательности между причиной и следствием. Оно просто указывает, что две переменные взаимосвязаны между собой в большей степени, чем это можно ожидать при случайном совпадении. Тем не менее, при соблюдении осторожности применение корреляционных методов при исследовании причинно-следственных отношений вполне оправдано. Следует избегать категоричных фраз типа «переменная X является причиной увеличения показателя Y ». Подобные утверждения следует формулировать как предположения, которые должны быть строго обоснованы теоретически.
Подробное описание математической процедуры для каждого коэффициента корреляции дано в учебниках по математической статистике [3]; [4]; [8]; [11] и др. Мы же ограничимся описанием возможности применения этих коэффициентов в зависимости от типа шкалы измерения.
Корреляция метрических переменных
Для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке, применяется коэффициент корреляции r -Пирсона . Сам коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y . Коэффициент линейной корреляции является параметрическим методом и его корректное применение возможно только в том случае, если результаты измерений представлены в шкале интервалов, а само распределение значений в анализируемых переменных отличается от нормального в незначительной степени. Существует множество ситуаций, в которых его применение целесообразно. Например: установление связи между интеллектом школьника и его успеваемостью; между настроением и успешностью выхода из проблемной ситуации; между уровнем дохода и темпераментом и т. п.
Коэффициент Пирсона находит широкое применение в психологии и педагогике. Например, в работах И. Я. Каплуновича [6, с. 115] и П. Д. Рабиновича, М. П. Нуждиной [9, с. 112] для подтверждения выдвинутых гипотез был использован расчет коэффициента линейной корреляции Пирсона.
При обработке данных «вручную» необходимо вычислить коэффициент корреляции, а затем определить p -уровень значимости (в целях упрощения проверки данных пользуются таблицами критических значений r xy , которые составлены с помощью этого критерия). Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем –1. Эти два числа +1 и –1 являются границами для коэффициента корреляции. Когда при расчете получается величина, большая +1 или меньшая –1, это свидетельствует, что произошла ошибка в вычислениях.
При вычислениях на компьютере статистическая программа (SPSS, Statistica) сопровождает вычисленный коэффициент корреляции более точным значением p -уровня.
Для статистического решения о принятии или отклонении H 0 обычно устанавливают α = 0,05, а для большого объема наблюдений (100 и более) α = 0,01. Если p ≤ α, H 0 отклоняется и делается содержательный вывод, что обнаружена статистически достоверная (значимая) связь между изучаемыми переменными (положительная или отрицательная – в зависимости от знака корреляции). Когда p > α, H 0 не отклоняется, содержательный вывод ограничен констатацией, что связь (статистически достоверная) не обнаружена.
Если связь не обнаружена, но есть основания полагать, что связь на самом деле есть, следует проверить возможные причины недостоверности связи.
Нелинейность связи – для этого проанализировать график двумерного рассеивания. Если связь нелинейная, но монотонная, перейти к ранговым корреляциям. Если связь не монотонная, то делить выборку на части, в которых связь монотонная, и вычислить корреляции отдельно для каждой части выборки, или делить выборку на контрастные группы и далее сравнивать их по уровню выраженности признака.
Наличие выбросов и выраженная асимметрия распределения одного или обоих признаков. Для этого необходимо посмотреть гистограммы распределения частот обоих признаков. При наличии выбросов или асимметрии исключить выбросы или перейти к ранговым корреляциям.
Неоднородность выборки (проанализировать график двумерного рассеивания). Попытаться разделить выборку на части, в которых связь может иметь разные направления.
Если же связь статистически достоверна, то прежде чем делать содержательный вывод, необходимо исключить возможность ложной корреляции:
- связь обусловлена выбросами . При наличии выбросов перейти к ранговым корреляциям или исключить выбросы;
- связь обусловлена влиянием третьей переменной . Если есть подобное явление, необходимо вычислить корреляцию не только для всей выборки, но и для каждой группы в отдельности. Если «третья» переменная метрическая – вычислить частную корреляцию.
Коэффициент частной корреляции r xy -z вычисляется в том случае, если необходимо проверить предположение, что связь между двумя переменными X и Y не зависит от влияния третьей переменной Z . Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием третьей переменной. Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи под влиянием общей причины. Например, общей причиной изменчивости двух переменных может являться возраст при изучении взаимосвязи различных психологических особенностей в разновозрастной группе. При интерпретации частной корреляции с позиции причинности следует быть осторожным, так как если Z коррелирует и с X и с Y , а частная корреляция r xy -z близка к нулю, из этого не обязательно следует, что именно Z является общей причиной для X и Y .
Корреляция ранговых переменных
Если к количественным данным неприемлем коэффициент корреляции r -Пирсона , то для проверки гипотезы о связи двух переменных после предварительного ранжирования могут быть применены корреляции r -Спирмена или τ -Кендалла . Например, в исследовании психофизических особенностей музыкально одаренных подростков И. А. Лавочкина [7, с. 149] был использован критерий Спирмена.
Для корректного вычисления обоих коэффициентов (Спирмена и Кендалла) результаты измерений должны быть представлены в шкале рангов или интервалов. Принципиальных отличий между этими критериями не существует, но принято считать, что коэффициент Кендалла является более «содержательным», так как он более полно и детально анализирует связи между переменными, перебирая все возможные соответствия между парами значений. Коэффициент Спирмена более точно учитывает именно количественную степень связи между переменными.
Коэффициент ранговой корреляции Спирмена является непараметрическим аналогом классического коэффициента корреляции Пирсона, но при его расчете учитываются не связанные с распределением показатели сравниваемых переменных (среднее арифметическое и дисперсия), а ранги. Например, необходимо определить связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном».
Коэффициент Спирмена широко используется в психологических исследованиях. Например, в работе Ю. В. Бушова и Н. Н. Несмеловой [1]: для изучения зависимости точности оценки и воспроизведения длительности звуковых сигналов от индивидуальных особенностей человека был использован именно он.
Так как этот коэффициент – аналог r -Пирсона, то и применение его для проверки гипотез аналогично применению коэффициента r -Пирсона. То есть проверяемая статистическая гипотеза, порядок принятия статистического решения и формулировка содержательного вывода – те же. В компьютерных программах (SPSS, Statistica) уровни значимости для одинаковых коэффициентов r -Пирсона и r -Спирмена всегда совпадают.
Преимущество коэффициента r -Спирмена по сравнению с коэффициентом r -Пирсона – в большей чувствительности к связи. Мы используем его в следующих случаях:
- наличие существенного отклонения распределения хотя бы одной переменной от нормального вида (асимметрия, выбросы);
- появление криволинейной (монотонной) связи.
Ограничением для применения коэффициента r -Спирмена являются:
- по каждой переменной не менее 5 наблюдений;
- коэффициент при большом количестве одинаковых рангов по одной или обеим переменным дает огрубленное значение.
Коэффициент ранговой корреляции τ -Кендалла является самостоятельным оригинальным методом, опирающимся на вычисление соотношения пар значений двух выборок, имеющих одинаковые или отличающиеся тенденции (возрастание или убывание значений). Этот коэффициент называют еще коэффициентом конкордации . Таким образом, основной идеей данного метода является то, что о направлении связи можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по X совпадает по направлению с изменением по Y , это свидетельствует о положительной связи, если не совпадает – об отрицательной связи, например, при исследовании личностных качеств, имеющих определяющее значение для семейного благополучия. В этом методе одна переменная представляется в виде монотонной последовательности (например, данные мужа) в порядке возрастания величин; другой переменной (например, данные жены) присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов.
При подсчете τ- Кендалла «вручную» данные сначала упорядочиваются по переменной X . Затем для каждого испытуемого подсчитывается, сколько раз его ранг по Y оказывается меньше, чем ранг испытуемых, находящихся ниже. Результат записывается в столбец «Совпадения». Сумма всех значений столбца «Совпадение» и есть P – общее число совпадений, подставляется в формулу для вычисления коэффициента Кендалла, который более прост в вычислительном отношении, но при возрастании выборки, в отличие от r -Спирмена, объем вычислений возрастает не пропорционально, а в геометрической прогрессии. Так, например, при N = 12 необходимо перебрать 66 пар испытуемых, а при N = 489 – уже 1128 пар, т. е. объем вычислений возрастает более чем в 17 раз. При вычислениях на компьютере в статистической программе (SPSS, Statistica) коэффициент Кендалла обсчитывается аналогично коэффициентам r -Спирмена и r -Пирсона. Вычисленный коэффициент корреляции τ -Кендалла характеризуется более точным значением p -уровня.
Применение коэффициента Кендалла является предпочтительным, если в исходных данных имеются выбросы.
Особенностью ранговых коэффициентов корреляции является то, что максимальным по модулю ранговым корреляциям (+1, –1) не обязательно соответствуют строгие прямо или обратно пропорциональные связи между исходными переменными X и Y : достаточна лишь монотонная функциональная связь между ними. Ранговые корреляции достигают своего максимального по модулю значения, если большему значению одной переменной всегда соответствует большее значение другой переменной (+1), или большему значению одной переменной всегда соответствует меньшее значение другой переменной и наоборот (–1).
Проверяемая статистическая гипотеза, порядок принятия статистического решения и формулировка содержательного вывода те же, что и для случая r -Спирмена или r -Пирсона.
Если статистически достоверная связь не обнаружена, но есть основания полагать, что связь на самом деле есть, следует сначала перейти от коэффициента
r -Спирмена к коэффициенту τ -Кендалла (или наоборот), а затем проверить возможные причины недостоверности связи:
- нелинейность связи : для этого посмотреть график двумерного рассеивания. Если связь не монотонная, то делить выборку на части, в которых связь монотонная, или делить выборку на контрастные группы и далее сравнивать их по уровню выраженности признака;
- неоднородность выборки : посмотреть график двумерного рассеивания, попытаться разделить выборку на части, в которых связь может иметь разные направления.
Если же связь статистически достоверна, то прежде чем делать содержательный вывод, необходимо исключить возможность ложной корреляции (по аналогии с метрическими коэффициентами корреляции).
Корреляция дихотомических переменных
При сравнении двух переменных, измеренных в дихотомической шкале, мерой корреляционной связи служит так называемый коэффициент j, который представляет собой коэффициент корреляции для дихотомических данных.
Величина коэффициента φ лежит в интервале между +1 и –1. Он может быть как положительным, так и отрицательным, характеризуя направление связи двух дихотомически измеренных признаков. Однако интерпретация φ может выдвигать специфические проблемы. Дихотомические данные, входящие в схему вычисления коэффициента φ, не похожи на двумерную нормальную поверхность, следовательно, неправильно считать, что интерпретируемые значения r xy =0,60 и φ = 0,60 одинаковы. Коэффициент φ можно вычислить методом кодирования, а также используя так называемую четырехпольную таблицу или таблицу сопряженности.
Для применения коэффициента корреляции φ необходимо соблюдать следующие условия:
- сравниваемые признаки должны быть измерены в дихотомической шкале;
- число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
Данный вид корреляции рассчитывают в компьютерной программе SPSS на основании определения мер расстояния и мер сходства. Некоторые статистические процедуры, такие как факторный анализ, кластерный анализ, многомерное масштабирование, построены на применении этих мер, а иногда сами представляют добавочные возможности для вычисления мер подобия.
В тех случаях когда одна переменная измеряется в дихотомической шкале (переменная X ), а другая в шкале интервалов или отношений (переменная Y ), используется бисериальный коэффициент корреляции , например, при проверке гипотез о влиянии пола ребенка на показатель роста и веса. Этот коэффициент изменяется в диапазоне от –1 до +1, но его знак для интерпретации результатов не имеет значения. Для его применения необходимо соблюдать следующие условия:
- сравниваемые признаки должны быть измерены в разных шкалах: одна X – в дихотомической шкале; другая Y – в шкале интервалов или отношений;
- переменная Y имеет нормальный закон распределения;
- число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
Если же переменная X измерена в дихотомической шкале, а переменная Y в ранговой шкале (переменная Y ), можно использовать рангово-бисериальный коэффициент корреляции , который тесно связан с τ-Кендалла и использует в своем определении понятия совпадения и инверсии. Интерпретация результатов та же.
Проведение корреляционного анализа с помощью компьютерных программ SPSS и Statistica – простая и удобная операция. Для этого после вызова диалогового окна Bivariate Correlations (Analyze>Correlate> Bivariate…) необходимо переместить исследуемые переменные в поле Variables и выбрать метод, с помощью которого будет выявляться корреляционная связь между переменными. В файле вывода результатов для каждого рассчитываемого критерия содержится квадратная таблица (Correlations). В каждой ячейке таблицы приведены: само значение коэффициента корреляции (Correlation Coefficient), статистическая значимость рассчитанного коэффициента Sig, количество испытуемых.
В шапке и боковой графе полученной корреляционной таблицы содержатся названия переменных. Диагональ (левый верхний – правый нижний угол) таблицы состоит из единиц, так как корреляция любой переменной с самой собой является максимальной. Таблица симметрична относительно этой диагонали. Если в программе установлен флажок «Отмечать значимые корреляции», то в итоговой корреляционной таблице будут отмечены статистически значимые коэффициенты: на уровне 0,05 и меньше – одной звездочкой (*), а на уровне 0,01 – двумя звездочками (**).
Итак, подведем итоги: основное назначение корреляционного анализа – это выявление связи между переменными. Мерой связи являются коэффициенты корреляции, выбор которых напрямую зависит от типа шкалы, в которой измерены переменные, числа варьирующих признаков в сравниваемых переменных и распределения переменных. Наличие корреляции двух переменных еще не означает, что между ними существует причинная связь. Хотя корреляция прямо не указывает на причинную связь, она может быть ключом к разгадке причин. На ее основе можно сформировать гипотезы. В некоторых случаях отсутствие корреляции имеет более глубокое воздействие на гипотезу о причинной связи. Нулевая корреляция двух переменных может свидетельствовать, что никакого влияния одной переменной на другую не существует.
🎥 Видео
Коэффициент ранговой корреляции Спирмена в MS Excel. Функция РАНГ.СРСкачать

Расчет коэффициента корреляции в ExcelСкачать

КОРРЕЛЯЦИЯ Спирмена Пирсона STATISTICA #08Скачать

Ранговая корреляция СпирменаСкачать

Коэффициент корреляции Пирсона, 2 способа вычисленияСкачать

Расчет корреляции Спирмена в SPSSСкачать

Коэффициент корреляции ПирсонаСкачать

Критерий корреляции СпирменаСкачать

Расчет корреляции Пирсона в SPSSСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Как посчитать коэффициенты корреляции в SPSSСкачать

Коэффициенты корреляции в ExcelСкачать