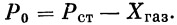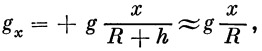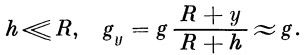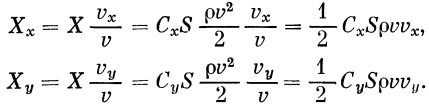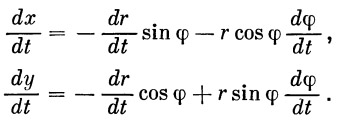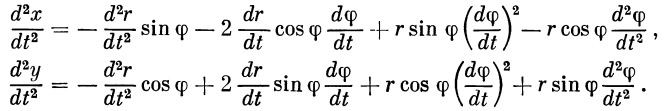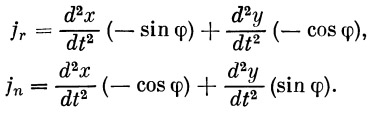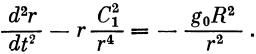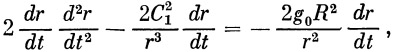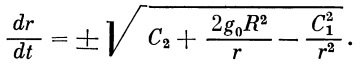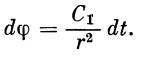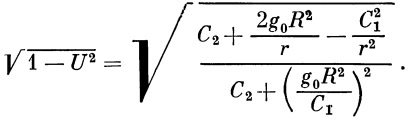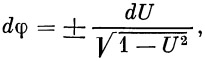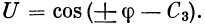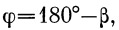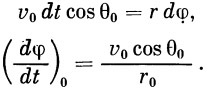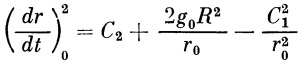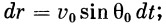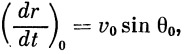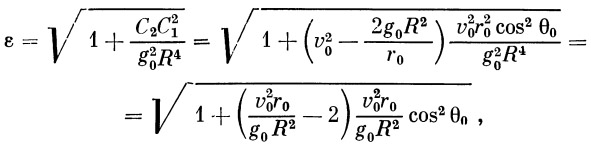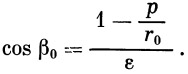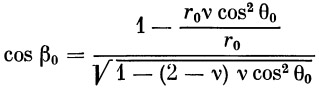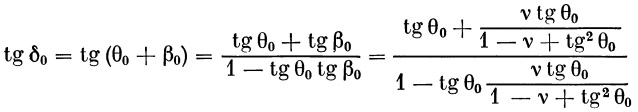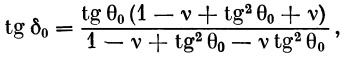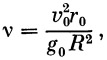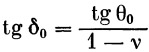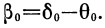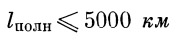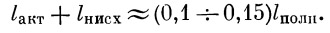Если угол бросания отличается от оптимального, то можно указать совокупность значений щ и во, обеспечивающих заданную дальность пассивного участка Lf. На рис. 3.6 и 3.7 приведены начальные условия стрельбы при ?о = 1 (когда радиусы начальной и конечной точек совпадают) и /’о = 1.06 (перепад высот между начальной и конечной точками порядка 350 км). Видно, что при /’о = 1 -Г 1.06 и 0о = 20° 40°
различие в потребных величинах начального параметра уо невелико (А//о уо при углах бросания во — 20° -г 40°, то для дальностей Lf уо. Значения Уо > 1 не рассматривались.
Одной из наиболее важных характеристик движения является самая высокая над Землей точка полета ГЧ (апогей). Радиус апогея га вместе с дальностью пассивного участка определяет основные геометрические соотношения траектории. Найдем угловую дальность Фа от начальной точки до апогея, а затем вычислим радиус апогея га (рис. 3.2).
Рис. 3.7. Параметры траектории стрельбы при го = 1.06 Угловая дальность Ф„ определяется из условия
где F(r, Ф) = 0 —уравнение (3.1.19). Последнее равенство выполняется при dF/dФ = 0. Дифференцируя (3.1.19) по Ф, получим после сокращений
Подставим (3.2.12) в уравнение (3.1.19) и в результате несложных преобразований придем к квадратному уравнению относительно г:
Решая его, найдем
Перед радикалом выбран знак минус, который обеспечивает минимальное значение г = го/ги и тем самым максимальное значение относительного радиуса
так как го = const.
Построенные на рис. 3.6 и 3.7 зависимости относительного радиуса апогея га соответственно для ?о = 1.0 и 1.06 показывают, что величина /’о слабо влияет на га. Действительно, различие А (Я = Яе)
Угол наклона траектории в точке падения 0/ определим с помощью интеграла площадей согласно условию
Отсюда следует, что
(знак минус взят с учетом падения ГЧ на нисходящей траектории). При п;> = 1 из соотношений (3.2.13) и (3.2.14) имеем
Этот результат легко объясняется с учетом симметрии эллиптической траектории полета ГЧ на пассивном участке.
Необходимо сделать одно замечание. Хотя неучет атмосферы мало сказывается на дальности полета ГЧ но сравнению с траекторией в реальных условиях, однако величины гу- и в/-, вычисленные по формулам (3.2.13), (3.2.14), могут существенно отличаться от действительных значений из-за сильного торможения ГЧ в нижних плотных слоях атмосферы, начиная с высот 30 -г 40 км.
Вычислим время полета ГЧ но эллиптической траектории от начальной точки до точки падения (или любой другой точки, радиус которой задан). Из дифференциального уравнения (3.1.9) имеем
Проинтегрируем левую и правую части (3.2.15), причем время будет меняться от О до //•, а угловая дальность —от 0 до Фу:
Выразим г из уравнения траектории (3.1.19) 
Введем следующие обозначения:
Тогда получим
Уравнение (3.2.19) эквивалентно (3.1.19) и определяет коническое сечение, один из фокусов которого совпадает с центром Земли. При выводе уравнения (3.2.19) не делалось никакого предположения относительно класса движения, поэтому оно справедливо для любой траектории (эллиптической, параболической, гиперболической), хотя, как уже отмечалось, полет ГЧ происходит по эллиптической траектории.
После подстановки (3.2.19) в (3.2.16) имеем
Для вычисления интеграла (3.2.20) перейдем к новой переменной х, которая связана с Ф условием
Дифференцируя левую и правую части (3.2.21), найдем
С помощью (3.2.21) получим
и для установления однозначной связи между Ф и х выберем знак минус. Тогда 
Подставим полученные соотношения (3.2.23) и (3.2.24) в (3.2.20) и вычислим интеграл:
Прежде чем подставить пределы, проведем некоторые вспомогательные выкладки. Сначала найдем
где
Далее, из соотношений (3.2.22) с учетом выбранного знака минус и (3.2.24) имеем
или, используя (3.2.26),
Теперь запишем интеграл энергии (3.1.4) в виде
а затем с помощью параметра (3.2.17) и эксцентриситета (3.2.18) вычислим
Сравнивая это соотношение с (3.2.28), получим
или
Учитывая уравнение (3.2.19), запишем окончательно
Из сравнения формул (3.2.24) и (3.2.29) имеем 
Следовательно, с учетом знака в формуле (3.2.27):
Подставим теперь соотношение (3.2.27) в (3.2.25), тогда получим
Постоянный множитель в (3.2.31) можно выразить через начальные параметры движения, используя формулы (3.1.8), (3.2.17), (3.2.18):
Итак, окончательная формула для вычисления времени полета ГЧ по эллиптической траектории от начальной точки до точки падения (на нисходящей ветви) имеет следующий вид [3.1]:
Входящие сюда величины иу и 0/ вычисляются но формулам (3.2.13) и (3.2.14). В частном случае, когда ?о = го/Я = 1, имеем и/ = щ и ву = — во, поэтому
Видео:Лекция 2 | Динамика полетаСкачать

13 уравнения движения ла большой дальности активный участок пассивный участок
С.П. Королёв
Основы проектирования
баллистических ракет дальнего действия
(курс лекций)
МВТУ ИМ. БАУМАНА 1949
ЛЕКЦИЯ ПЕРВАЯ
Вторая, основная, часть курса лекций, прочитанного С. П. Королевым в 1949 г. на Высших инженерных курсах, организованных при Московском высшем техническом училище им. Н. Э. Баумана для переподготовки инженеров различных специальностей для работы в ракетостроительной промышленности. Этот курс, в котором был использован и обобщен опыт работы ОКБ по созданию ракет, сразу же изданный в МВТУ в качестве учебного пособия, явился первым в мире систематизированным, достаточно подробным и завершенным курсом основ проектирования жидкостных БРДД, и поэтому он лег в основу преподавания этой дисциплины в институтах, готовящих специалистов по ракетостроению. В настоящем сборнике* работа печатается по изданию МВТУ, 1949 г.
[* Имеется ввиду сборник «Творческое наследие академика Сергея Павловича Королева. Избранные труды и документы» / Под общей редакцией академика М. В. Келдыша — Издательство «Наука», 1980 г.]
1. Баллистический анализ
Обычно основной задачей, которая ставится перед проектантом ракеты дальнего действия, является переброска требуемого боевого груза на заданное расстояние.
В зависимости от метода конструктивного решения поставленной задачи можно указать три основных класса таких ракетных аппаратов:
1-й класс — ракеты так называемой нормальной баллистической схемы, например по типу ракеты с двумя подвесными баками (ракета 2ПБ).
2-й класс — составные ракеты. В этом случае система состоит из ракеты несущей и ракеты несомой, которая отделяется от первой на некоторой высоте. Число ступеней отделения, вообще говоря, может быть сколь угодно велико.
Схемы таких ракет были разработаны К. Э. Циолковским.
3-й класс — крылатые ракеты, использующие подъемную силу крыльев для увеличения дальности полета за счет планирования на пассивном участке полета. В некоторых случаях полет с крыльями может происходить и с работающим двигателем.
В дальнейшем изложении в основном будут рассматриваться главнейшие вопросы проектирования ракет 1-го класса Нормальной баллистической схемы.
В первую очередь рассмотрим инженерную методику расчета траектории и определения основных летных характеристик ракеты.
Вывод уравнений движения ракеты в самом общем виде, с учетом всех факторов, достаточно сложен. Практика работы наших конструкторских бюро показала, что принятая упрощенная инженерная методика расчета траектории вполне оправдывает себя с допустимой степенью точности. Произведенные сравнительные расчеты, а также обработка результатов пусков ракет показывают, что сумма неточностей лежит в пределах порядка 2—3%. Необходимо учитывать также, что в процессе проектирования ряд величин и параметров выбирается с возможными отклонениями в значительно более широких пределах, чем приведенные выше цифры.
1.1. Расчет активного участка
Уравнения движения центра тяжести ракеты в декартовых осях, неподвижно связанных с Землей, мы пишем при следующих основных допущениях.
1. Предполагается, что ось ракеты совпадает с касательной к траектории центра тяжести, т. е. векторы скорости полета ракеты V и реактивной силы P совпадают. Это допущение означает, что мы будем полагать угол атаки а ракеты равным нулю, а следовательно, пренебрегать влиянием на траекторию аэродинамической подъемной силы.
Сравнение приближенных расчетов при указанном допущении с расчетами по точной методике, а также с результатами экспериментов показывает, что ошибка в значении скорости в приближенном расчете не выше 1—1,5%. Ошибка в величине координат, хотя и несколько больше (вследствие изменения формы траектории), однако ею также вполне можно пренебречь при практическом проектировании.
2. Далее, коэффициент силы лобового сопротивления ракеты Сх принимается постоянным, не зависящим от угла атаки.
3. Пренебрегаем изменением силы сопротивления газовых рулей при их отклонении. Ошибки, получающиеся из-за указанного допущения, невелики и при подсчете скорости не превосходят
Следует отметить, что абсолютное значение сопротивления рулей необходимо брать с учетом обгорания их.
Для ракеты 2ПБ потери тяги в этом случае составят порядка 1,4-1,8 т .
4. Пренебрегаем влиянием вращения Земли, что вызывает ошибки, меньшие 1% для рассматриваемой нами ракеты.
5. Полагаем секундный расход топлива неизменным в течение всего времени работы двигателя.
G — вес ракеты ( кг ),
m — масса ракеты ( кг • сек 2 / м ),
g — ускорение силы тяжести ( м / сек 2 ),
v — скорость полета ( м / сек ),
X — сила лобового сопротивления ( кг ),
θ — угол касательной к траектории с осью х .
Проектируя действующие силы на направление касательной к траектории и относя их к массе m , получаем следующее уравнение движения (рис. 1):
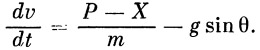 | (1) |
К уравнению (1) мы добавляем два уравнения:
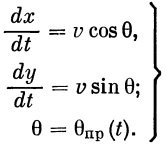 | (2) |
Уравнения (1) и (2) необходимо дополнить уравнением программы, обеспечивающей заданную форму траектории и нужный угол θ в конце активного участка.
Зависимость θ = θ пр( t ) задается графически или в виде таблицы.
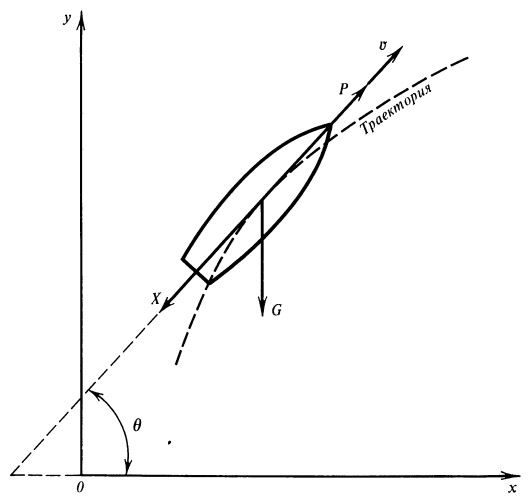 Рис. 1. К выводу уравнений движения |
Расчеты по упрощенной схеме, представленной уравнениями (1) и (2), достаточны для проверки основных проектных характеристик.
В уравнение (1) входят величины Р , X и m , о которых кратко можно сказать следующее.
Тяга Р при полете ракеты может определяться по формуле
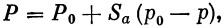 | (3) |
где Р 0 — тяга, замеренная на стенде Р ст, с учетом силы сопротивления неотклоненных газовых рулей Х газ:
Сопротивление неотклоненных газовых рулей ракеты 2ПБ составляет в среднем 1400—1800 кг .
В случае отклонения газовых рулей их сопротивление может резко увеличиваться. Однако при этом необходимо иметь в виду также и то обстоятельство, что геометрия газовых рулей по мере работы двигателя сильно изменяется вследствие их постепенного обгорания.
Поэтому вопрос о величине дополнительного сопротивления пока не может быть решен достаточно точно, и во всех расчетах можно ориентироваться на приведенные цифры.
Sa означает площадь выходного сечения сопла, р 0 — атмосферное давление у поверхности Земли, р — давление в атмосфере на данной высоте.
Масса ракеты может определяться по формуле
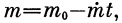 | (4) |
где m — масса ракеты в момент t , m 0 — масса ракеты в момент t =0, ṁ — секундный массовый расход топлива, t — время в секундах.
Сила лобового сопротивления ракеты определяется по формуле
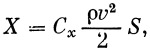 | (5) |
где С х — коэффициент силы лобового сопротивления, ρ — плотность воздуха на высоте полета (( кг / м 4 )• сек 2 ), v — скорость полета ( м / сек ), S — площадь миделя ракеты ( м 2 ).
Все численные значения основных величин, а также интегрирование системы уравнений (1) и (2) нами здесь не рассматриваются, так как вопросу численного интегрирования указанных уравнений будет посвящено специальное практическое занятие.
1.2. Пассивный участок полета
Пассивный, или свободный, участок полета ракеты, т. е. движение ее после окончания работы двигателя, является движением по инерции. Живая сила, приобретенная ракетой на активном участке, расходуется на преодоление сопротивления воздуха и силы тяготения.
Мы разбиваем расчет свободного участка на две части. В первой части учитываем действие сопротивления воздуха и поля тяготения, а во второй — ограничиваемся учетом лишь поля тяготения. Система координат и обозначения, принимаемые нами при расчете первого участка свободного полета, поясняются на рис.
2. Если обозначить индексами х и у проекции соответствующих векторов на оси координат, то уравнения движения центра тяжести ракеты примут вид
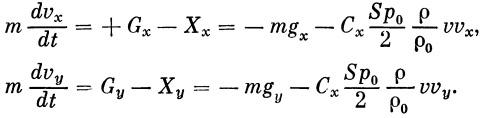 | (6) |
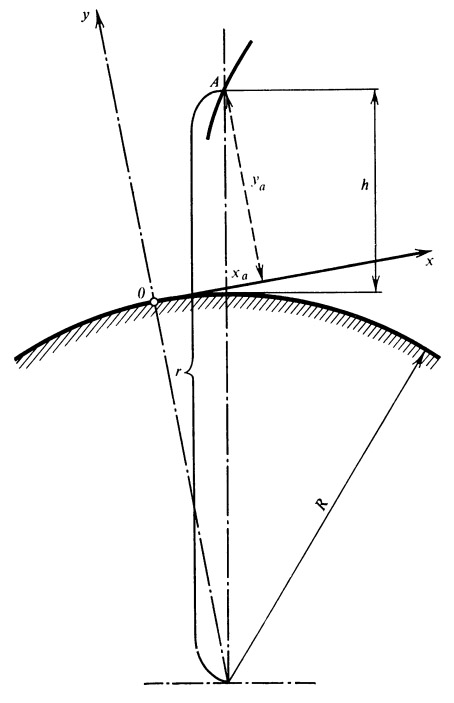 Рис. 2. Система координат и основные обозначения для первого участка свободного полета |
Значения Х х и Х у получаются [в виде]
Разделив уравнения (6) на m и добавляя два кинематических уравнения, получим систему уравнений (7), достаточную для проведения численного интегрирования и определения параметров интересующего нас участка:
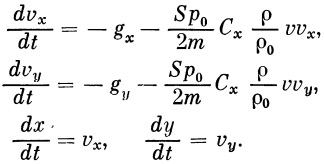 | (7) |
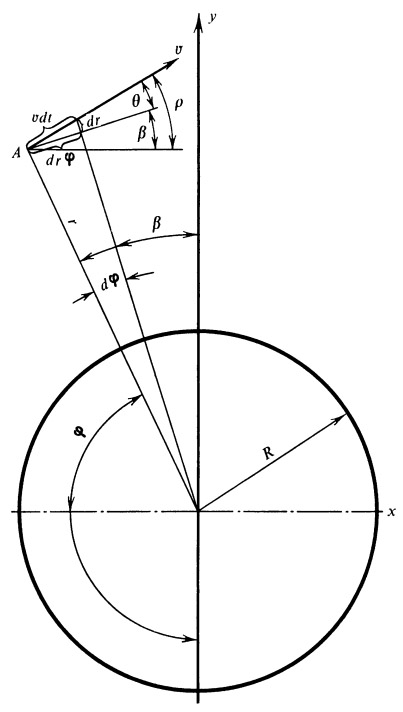 Рис. 8. Система координат и основные обозначения для второго участка свободного полета |
Высота h в случае необходимости может быть определена по формуле
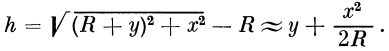 | (8) |
В результате численного интегрирования системы уравнений (7) мы получаем координаты центра тяжести ракеты, ее скорость, а также угол наклона касательной к траектории для момента времени, после которого силой сопротивления воздуха можно пренебречь.
Эти параметры будут начальными условиями для расчета второй части свободного участка, где учитываем только силы тяготения. К расчету этого участка мы и перейдем. Принятые обозначения поясняются рис. 3.
Для движущейся точки А могут быть написаны следующие соотношения:
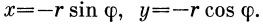 | (9) |
Дифференцируя еще один раз, имеем
Обозначим: j r — ускорение ракеты по направлению радиус-вектора; j n — ускорение ракеты по нормали к радиус-вектору. Очевидно, что
После подстановки в эти уравнения значений d 2 x / dt 2 и d 2 y / dt 2 и соответствующих преобразований, получим
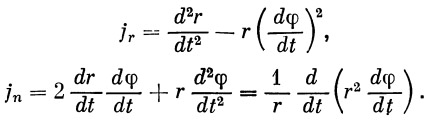 | (10) |
Напишем уравнение движения нашей ракеты в полярной системе координат ( r , φ ). Учитывая, что
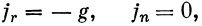 | (11) |
где g — ускорение на высоте полета ракеты, и подставляя в уравнения (10) значения j r и j n из уравнений (10), получим
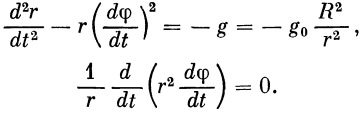 | (12) |
Из последнего уравнения следует известный закон Кеплера
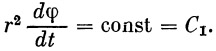 | (13) |
Из уравнения (13) мы найдем dφ / dt и, подставляя его в первое уравнение системы (12), получим
Умножим обе части последнего уравнения на 2 ( dφ / dt ):
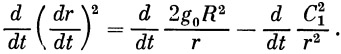 | (14) |
Интегрируем уравнение (14):
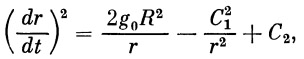 | (15) |
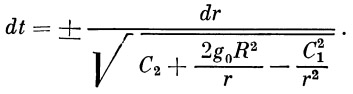 | (16) |
Из уравнения (13) имеем
Подставляем сюда выражение для dt из (16):
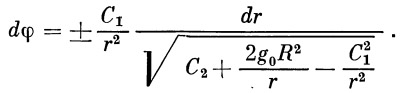 | (17) |
Для интегрирования уравнения (17) введем подстановку
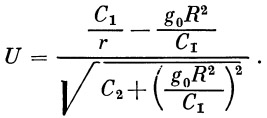 | (18) |
(18)
Теперь вместо дифференциального уравнения (17) мы можем написать следующее:
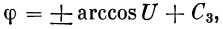 | (19) |
Из выражения (18) находим значение радиуса r :
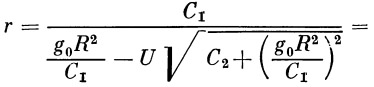 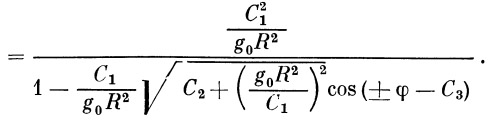 | (20) |
Выбирая соответствующим образом начало отсчета угла φ , из последней формулы можно получить
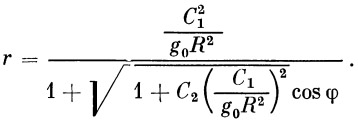 | (21) |
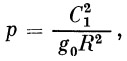 | (22) |
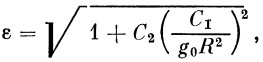 | (23) |
то из (21) следует
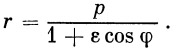 | (24) |
Это уравнение представляет собой уравнение эллипса. Так как ось у проходит через вершину траектории, то введем в качестве координатного (полярного) угла угол β вместо угла φ :
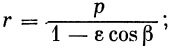 | (25) |
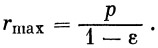 | (25′) |
Определим постоянные величины, введенные в процессе интегрирования.
У нас имеются две произвольные постоянные C 1 и С 2 и два сокращенных обозначения р и ε .
Если момент начала свободного участка ракеты в поле тяготения (без учета сил сопротивления воздуха) совместить с моментом конца сгорания топлива, то тогда параметры точки конца горения будут одновременно начальными условиями для свободного участка.
Пусть ракета в начале свободного участка находилась в точке А (см. рис. 3). Всем величинам, характеризующим положение и скорость ракеты в этот момент, мы присваиваем индекс «нуль». Тогда из рис. 3 легко устанавливаем, что
Сопоставляя с уравнением (13), получим
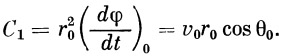 | (26) |
Далее, из уравнения (15) имеем
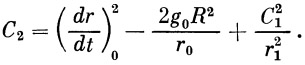 | (27) |
Величина ( dr / dt )0 определяется из рис. 3:
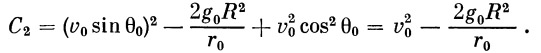 | (28) |
Константа С 3 нами исключена из рассмотрения надлежащим выбором начала координат, что учитывается формулой (21).
Прежде чем выразить оставшиеся константы через известные величины, введем обозначение, чрезвычайно важное в дальнейших расчетах:
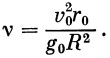 | (29) |
Здесь, как и выше, g 0 означает ускорение на поверхности Земли, v 0 и r 0 — скорость ракеты и ее радиус-вектор в конце активного участка.
Согласно обозначению (22), находим
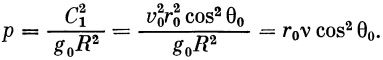 | (30) |
В соответствии с (23) получим
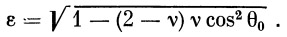 | (31) |
Далее, из выражения (25), решенного относительно β 0,
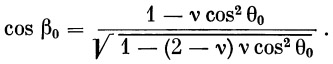 | (32) |
Переходя от cos β 0 к tg β 0 по формуле
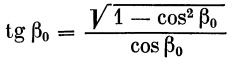 | (33) |
и подставляя в формулу (33) выражение для cos β 0 из (32), получим
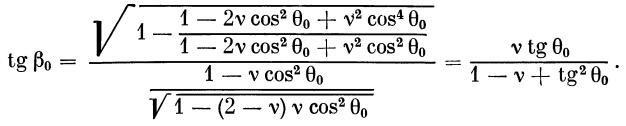 | (34) |
Если равенством δ 0= θ 0+ β 0 ввести угол δ 0, то формулы можно значительно упростить:
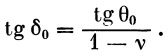 | (35) |
Полученные формулы позволяют сразу решить все интересующие нас вопросы, связанные с расчетом свободного участка.
По известным начальным условиям (конец активного участка) вычисляется параметр v по формуле B9)
далее по формуле
находим угол δ 0 и вычисляем β 0:
По известному углу B 0 определяем «эллиптическую» дальность l эл. Параметры движения в конце эллиптического участка (точка В ) принимаются за исходные для расчета дальности нисходящего участка траектории l нисх. Обозначения поясняются рис. 4.
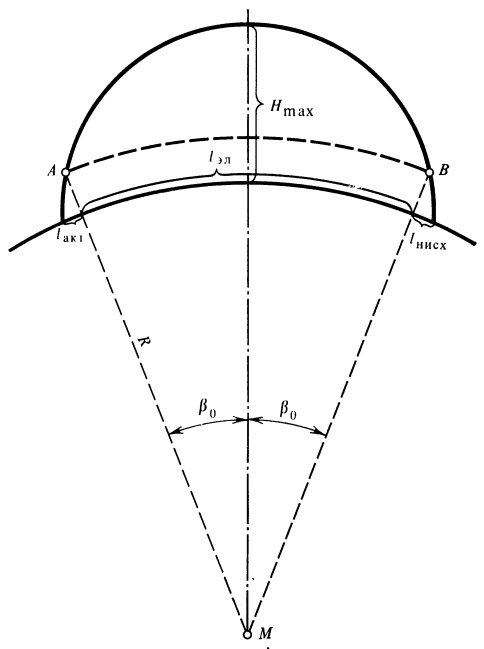 Рис. 4. К расчету дальности полета |
«Эллиптическая» дальность вычисляется по следующей формуле:
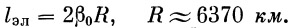 | (36) |
Полная дальность ракеты вычисляется по формуле
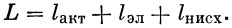 | (37) |
Максимальная высота подъема, т. е. вершина траектории, определится выражением
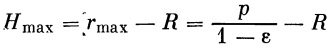 | (38) |
(на основании формулы (25′))
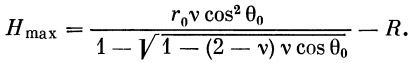 | (39) |
На начальной стадии проектирования необходимость проведения серии подсчетов даже по таким сравнительно простым формулам все-таки связана с затратой значительного времени.
Поэтому для прикидочных расчетов может быть рекомендована простая номограмма, позволяющая с достаточным приближением и быстро производить такие расчеты.
Номограмма приведена на рис. 5.
При пользовании предложенной номограммой необходимо сделать следующее замечание.
Сравнение величин l акт+ l нисх с величиной l полн показывает, что до дальностей
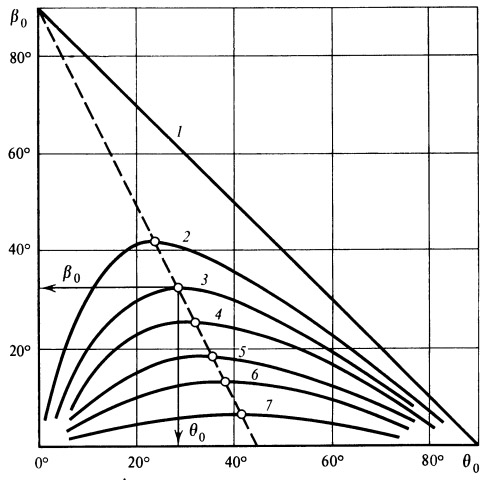 Рис. 5. Номограмма для расчета дальности 1 — v = l; 2 — 0,8; 3 — 0,7; 4 — 0,6; 5 — 0,5; 6 — 0,4; 7 — 0,2 |
Поэтому с достаточным приближением можем считать
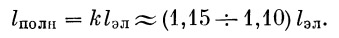 | (40) |
Учитывая последнее обстоятельство, при определении основных проектных параметров мы можем пользоваться номограммой, построенной только для дальности эллиптического участка.
Рассмотрим некоторые задачи, решаемые с помощью номограммы.
1. Пусть нам задана величина v . Требуется определить возможную максимальную дальность. По номограмме при заданном v из условия оптимума находим β 0 и θ 0, затем по формуле (36) определяем l эл, по формуле (40) находим l полн.
2. Пусть задано l полн. Требуется определить оптимальные параметры. Зная l полн, по формуле (40) находим l эл, а по формуле (36) определяем β 0
Далее используем номограмму: задаваясь найденным углом β 0 определяем v min и соответственно оптимальный угол θ 0. По величине v min находим минимально необходимую начальную скорость v 0.
3. Задано θ 0. Требуется определить v 0, при которой этот угол имеет оптимальное значение.
Требование определения v 0, удовлетворяющей поставленной задаче, аналогично отысканию такого v , при котором заданный угол дает максимальное значение дальности.
По номограмме легко видеть, что оптимальные условия можно найти не для любого угла θ , а только для θ 0≤45°.
Следует подчеркнуть, что ценность номограммы заключается в получении первого ориентировочного подсчета основных величин лишь в начальной стадии проектирования.
Видео:3-2 Численное моделирование полёта ракетыСкачать

Пассивный участок траектории ЛА
Расчёт траекторных параметров на конце пассивного участка полёта ЛА произведён с помощью программы, созданной в ОПП «Matlab». Шаг интегрирования равен 0,01. Результаты представлены в табл. 5. Входными данными являются параметры движения в конце активного участка.
Видео:Выполнялка 133. Разрыв снаряда, выпущенного из пушки вертикально вверх...Скачать

Формирование случайных процессов на ЭВМ
При исследовании динамики систем методом моделирования возникает задача воспроизведения случайных процессов с заданными статистическими свойствами. Эту задачу можно решить путем пропускания белого шума через формирующий фильтр.
В общем случае случайную функцию можно считать заданной, если известны все многомерные законы распределения для любых значений из области аргумента t. В рамках корреляционной теории случайную функцию характеризуют математическим ожиданием:
и корреляционной функцией:
где — центрированная случайная функция, f(x/t), -одномерный и двумерный дифференциальные законы распределения.
Корреляционная функция при значении представляет собой дисперсию случайного процесса:
Если случайная функция x(t) является стационарной, то справедливы соотношения:
Случайная функция x(t) обладает эргодическим свойством, если ее характеристики m(x), могут быть определены осреднением по времени одной реализации достаточной длительности. Достаточным условием эргодичности стационарной случайности функция является стремлением к нулю ее корреляционной функции:
Наряду с корреляционной функцией стационарную, случайную функцию можно характеризовать спектральной плотностью .
Спектральная плотность и корреляционная функция однозначно получаются друг из друга как прямое и обратное преобразования Фурье:
Спектральная плотность характеризует распределение дисперсии случайного процесса по частотам его гармонических составляющих:
При исследовании двух x(t), y(t) или более случайных процессов в рассмотрении вводятся взаимные корреляционные функции и взаимные спектральные плотности :
Стационарный, случайный процесс, обладающий постоянной спектральной плотностью:
принято называть белым шумом. Его корреляционная функция согласно (6)
Дисперсия такого случайного процесса, как следует из (7), равна бесконечности, поэтому определенный выше белый шум является математической абстракцией и физически не реализуем.
В практических задачах под белым шумом понимает случайный процесс, спектральная плотность которого постоянно в широком диапазоне частот перекрывают полосу пропускания исследуемой системы. В лабораторных исследованиях случайные процессы такого вида получаются с помощью специальных приборов-генераторов белого шума.
В основу метода получения из белого шума случайных процессов с различными спектральными плоскостями положено свойство динамической системы изменять спектральный состав входных воздействий. Для систем, динамические свойства которые описывают передаточной функцией Ф(p), формула, связывающая спектральные плотности входного x(t) и выходного y(t) сигналов, имеет вид:
Если входным сигналом является нормированный белый шум со спектральной плотностью , то спектральная плотность выходного сигнала:
Эта формула позволяет способ определения передаточной функции формирующего фильтра, преобразующего белый шум в случайный процесс с заданной спектральной плотностью. Для этого надо спектральную плотность представить в виде произведения двух комплексно сопряженных сомножителей:
Тогда передаточная функция формирующего фильтра находится по формуле:
Разложение (15) возможно, если спектральная плотность является дробно-рациональной функцией.
Горизонтальная (продольная) турбулентность атмосферы
Продольная турбулентность, действующая на ЛА, описывается стационарным случайным процессом с ковариационной функцией:
Для определения передаточной функции соответствующего формирующего фильтра найдем спектральную плотность:
Полученное выраженье запишем в формуле (15):
Отсюда, на основании (16), передаточная функция формирующего фильтра:
Таким образом, для получения случайного процесса с корреляционной функцией (17) надо пропустить белый шум через фильтр с передаточной функцией (19). Соответствующее дифференциальное уравнение имеет вид:
Вертикальная (поперечная) турбулентность атмосферы
Из экспериментальных данных следует, что вертикальные порывы ветра, действующие на ЛА, движущийся со скоростью V, описываются случайной функцией, корреляционная функция и спектральная плотность которой имеет вид:
где L- масштаб турбулентности,- среднеквадратическое отклонение, характеризующее интенсивность турбулентности.
Для получения из белого шума такого случайного процесса необходимо определить передаточную функцию формирующего фильтра. Для этого выражение (2) преобразуется к виду :

Отсюда находим передаточную функцию:
Дифференциальное уравнение, описывающее динамику фильтра, может быть записано в виде:
Для моделирования на компьютере приведем уравнение второго порядка (26) к системе двух уравнений первого порядка:


Определение характеристик стационарных процессов по реализациям
При работе динамической системы на ее входы действуют случайные сигналы, вероятные характеристики которые обычно известны. Во многих прикладных задачах вероятные характеристики случайных процессов определяются экспериментально путем обработки реализации этих процессов.
В работе считается, что заданы реализации случайного процессаx(t) в дискретном ряде точек:
Оценка математического ожидания рассчитывается по формуле:
Оценка дисперсии рассчитывается по формуле:
За оценку среднеквадратического отклонения можно принять:
Итоговая система дифференциальных уравнений движения БПЛА в турбулентной атмосфере


Где =N(0,1), — шаг интегрирования,

Графики распределения параметров турбулентной атмосферы:
Графики распределения основных параметров движения БПЛА:


Отклонение дальности от номинальной:
L(W = 0 м/с)= 6613.51 м
Исследование разброса дальности для различного числа пусков.
 Гистограммы распределения dL(N)
Выводы по проделанной работе В ходе выполнения курсовой работы была построена математическая модель неуправляемого реактивного снаряда с учетом следующих допущений:
По построенной математической модели была создана компьютерная модель полета снаряда, которая заключалась в написании программ реализующих методы численного интегрирования (Рунге — Кутта). В ходе вычислений были получены N — испытаний с учетом влияния турбулентности атмосферы, распределенные по нормальному закону. По этим данным была определена чувствительность дальности к действию ветра, а так же определены оценки математического ожидания, дисперсии и среднеквадратического отклонения, отклонения дальности от номинальной. Как видно из значений математического ожидания и графика распределения отклонения дальности распределение отклонения дальности близко к нормальному. 📺 ВидеоМатематическое моделирование - Лекция 1 (09.02.07)Скачать  Построение 13 угольника приближенное, tridecagon constructionСкачать  АУПО. Силы и моменты, действующие на летательный аппарат. Математическая модель.Скачать  Урок 106. Реактивное движениеСкачать  Лекция 1 | Динамика полетаСкачать  Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать  Семинар. Уравнение баланса напоров для участка магистрального нефтепроводаСкачать  Инерция | Физика 7 класс #13 | ИнфоурокСкачать  Центр тяжести. СамолетСкачать  Лекция по радиолокации. Инженер Степанов Ф.М.Скачать  Теоретическая механика. Лекция №1: Уравнения ЛагранжаСкачать  Введение в авиационную и ракетно-космическую технику от 23.11.20Скачать  Задание 34 вариант 13 (14, 15). Группа геометрических телСкачать  Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать  Подъёмная сила крыла ● 1Скачать  |