Потенциал действия (ПД), возникнув в одном участке нервной клетки быстро распространяется по всей поверхности. Распространение ПД обусловлено возникновением локальных токов, циркулирующих между возбужденным и невозбужденным участками клетки. Локальными называются токи, возникающие между невозбужденным и возбужденным участками нервного волокна, вследствие возникновения разности потенциалов между ними. На поверхности клетки локальный ток течет от невозбужденного участка к возбужденному; внутри клетки он течет в обратном направлении. Нервное волокно можно рассматривать как кабель, который характеризуется:
- электрической емкостью,
- сопротивлением мембраны,
- сопротивлением аксоплазмы и окружающей среды.
Распространение потенциала по нервному волокну описывается так называемым телеграфным уравнением, которое имеет вид:
Е = Е0·e –x/l; где: l — константа длины нервного волокна.
Так как, при х = l, Е = Е0 / e, то l — это расстояние, на котором потенциал Е уменьшается в e раз по сравнению с Е0.
Распространение потенциала действия имеет особенности, зависящие от типа нервных волокон. По безмякотному волокну, которое не имеет миэлиновой оболочки, распространение возбуждения будет затухающим и осуществляется за счет локальных токов.
Распространение потенциала действия по мякотным (покрытым миэлиновой оболочкой) осуществляется скачкообразно (сальтаторно) от одного перехвата Ранвье к другому.
Диапазон возможных значений скорости проведения в миелинизированных волокнах широк: от нескольких метров в секунду до 100 м/с. Мировой рекорд принадлежит миелинизированным аксонам креветки, которые проводят возбуждение быстрее 200 м/с. В нервной системе позвоночных нервы разделяются на группы по скорости проведения или по функции. В соответствии с теоретическими расчетами, скорость проведения в волокне должна быть пропорциональна его диаметру. Бойд и коллеги показали, что у млекопитающих скорость проведения (в м/с) для толстых миелинизированных волокон приблизительно равняется их внешнему диаметру (в м), помноженному на 6. Для более тонких волокон коэффициент пропорциональности приблизительно равен 4,5.
При функционировании тканей и органов, как и отдельных клеток, сопровождающемся электрической активностью, в организме создается электрическое поле. Так как организм является проводником, то два электрода, приложенные к разным участкам тела, регистрируют разность потенциалов. Зависимость от времени разности потенциалов, возникающей при функционировании данного органа или ткани, называется электрограммой. Названия электрограмм указывают на органы (ткани), функционирование которых приводит к появлению, регистрируемой разности потенциалов: электрокардиограмма (ЭКГ), электроэнцефалограмма (ЭЭГ), электромиограмма (ЭМГ) и т.д. Можно сформулировать две основные задачи изучения электрограмм:
- первая (прямая) заключается в выяснении механизма возникновения электрограмм,
- вторая (обратная, или диагностическая) — в выявлении состояния организма по характеру его электрограмм.
При изучении механизма возникновения электрограмм ткани и органы как источники электрического поля представляют в виде эквивалентного электрического генератора. Под ним подразумевается модельная физическая система, которая должна удовлетворять двум условиям:
- потенциалы, создаваемые генератором в различных точках должны соответствовать реальным величинам;
- при изменении параметров эквивалентного генератора должны происходить такие же изменения электрического поля как и в реальных электрограммах при соответствующем изменении в функционировании органа.
Видео:Уравнение движенияСкачать

Телеграфные уравнения
Получим соотношения между напряжением U и током I в линии передачи с ТЕМ-волной, которые позволят анализировать распространение электромагнитной волны в линии, не решая уравнения Максвелла. С этой целью рассмотрим небольшой отрезок коаксиальной линии длиной Дх (рис. 2.8).
Рис. 2.8. Отрезок коаксиальной линии.
Пунктир — линия интегрирования
Полагаем, что напряжение в сечении плоскости А равно Uv а в сечении плоскости Б — Ur Линию считаем не имеющей потерь, обладающей погонной индуктивностью L, и погонной емкостью С] (Lt, С, — это соответственно индуктивность и емкость линии длиной 1 м).
Воспользуемся интегральной записью второго уравнения Максвелла
где магнитный поток представим в виде
Здесь L — индуктивность отрезка линии, определяемая погонной индуктивностью Ь] и длиной Ах:
Контур интегрирования 1-2-3-4 изображен на рис. 2.8. Итак, с учетом (2.19)
Поскольку скалярное произведение векторов Edl = Edl х xcosa, где a — угол между векторами Ё и с1/, то
Учитывая связь напряженности электрического поля Е с потенциалом ср = -| Edx, запишем
Принимая во внимание (2.20), получаем 
В пределе при Ах—>• 0 окончательно запишем
Воспользуемся определением силы тока
где заряд Q = CU, С — емкость линии, определяемая погонной емкостью С, и длиной Ах, т.е. С = СДт.
Связь силы тока I с плотностью тока ] определяется следующим соотношением:
Выберем в качестве поверхности интегрирования цилиндрическую поверхность, охватывающую внутренний проводник коаксиальной линии (рис. 2.9).
Тогда Jy dS = J j d5 + Jy dS = /2 = А/ (интеграл по боко-
вой поверхности равен нулю) и
Окончательно при переходе к пределу при Ах —» 0 имеем
Уравнения (2.21) и (2.22) называют телеграфными. Их решение дает возможность найти ток / и напряжение U как функции времени и координаты х.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Решение телеграфных уравнений
Продифференцировав уравнение (2.21) по координате х, а уравнение (2.22) по времени t и исключив ток /, получим волновое уравнение для напряжения U:
Будем полагать для простоты, что к линии подводятся колебания одной частоты со. Тогда решение уравнения (2.23) может быть записано в виде монохроматических волн
где первое слагаемое в правой части уравнения описывает падающую волну, бегущую по линии в положительном направлении оси х, а второе слагаемое — отраженную волну, распространяющуюся в отрицательном направлении оси х.
В решении (2.24) С/пад, U — амплитуды падающей и отраженной волн (начальные фазы при t = 0 и х = 0 считаем равными нулю); р — постоянная распространения
v — скорость волны в линии
Волновое уравнение может быть записано и для тока 
Как было отмечено в параграфе 1.7, монохроматические волны удобно представлять в виде комплексных амплитуд
Связь между С/пад и 7пад можно получить, подставив в первое телеграфное уравнение (2.21) мгновенные значения напряжения и тока в линии передачи.
В результате будем иметь

где р = — — волновое сопротивление линии,
Аналогично можно найти связь U с 1‘.
Видео:7. Телеграфные уравненияСкачать

Распростанение ПД по нервному волокну
До середины XIX в. полагали, что электрические импульсы распространяются подобно электричеству по проводам, однако после того как Г. Гельмгольц в середине XIX в. получил для скорости распространения импульса по нервам величину 50 м/с, а впоследствии было установлено, что наибольшая скорость импульса по нервному волокну не превосходит 140 м/с, упрошенные аналогии пришлось пересмотреть. Электрический механизм генерации нервного импульса еще не означает, что его распространение осуществляется подобно проведению электрических сигналов по кабелю.

Рис. 43. Потенциалы действия на мембранах различных тканей, а — волокно гигантского аксона кальмара; б — мышечное волокно кролика; в — волокно электрического ската; г — волокно типического кардиомиоцита кролика [11]
Мы уже привыкли не удивляться тому, что природа сконструировала ряд устройств, которые достигли физического предела совершенства. Так, например, адаптированный к темноте глаз человека различает единичные кванты, а наш порог слышимости соответствует механическим смещениям барабанной перепонки всего на 10 радиусов атома водорода. Более чувствительный прибор физически невозможен — мы бы «слышали» молекулярные флуктуации воздуха вследствие теплового движения молекул при температуре 37 °C. Обоняние некоторых животных таково, что они «чувствуют» 1-2 молекулы в см 3 воздуха и т. д.
Тем не менее нервные проводники — исключительно плохие кабели. Технический кабель тем лучше, чем меньше у него сопротивление жилы и больше сопротивление изоляции. В распоряжении инженеров, например, для жилы могут использоваться металлы с удельным сопротивлением порядка 10’ 7 Ом-м и диэлектрики Ю 17 Ом-м -для изоляции. У природы выбор беднее: для жилы можно применить только цитоплазму, а для изоляции — фосфолипидную мембрану, причем тот и другой природные материалы на несколько порядков хуже технических. Вследствие «плохих» изоляционных свойств нервных проводников у них присутствуют огромные токи утечки через мембранную поверхность [11].
А. Ходжкин дал интересную иллюстрацию этих свойств распространения электрического сигнала: если специалист по электричеству посмотрит на нервную систему, то сразу увидит, что передача сигнала по нервным волокнам является огромной проблемой. Диаметр аксона в нерве варьирует от 0,1 до 20 мкм. Внутреннее содержимое содержит ионы и является неплохим проводником электричества. Однако волокно невелико и его продольное сопротивление очень высоко. Простой расчет показывает, что в волокне диаметром 1 мкм и сопротивлением 100 Ом/см удельное сопротивление составит около 10 ю Ом/см. Это означает, что электрическое сопротивление маленького нервного волокна длиной в 1 метр равно сопротивлению 1О 10 миль 0,2 мм медной проволоки, то есть проволоки длиной в десять раз больше, чем от Земли до Сатурна [17].
Рассмотрим процессы, которые происходят при распространении электрического импульса. Потенциал действия, возникнув в одном участке нервной клетки, быстро распространяется по всей ее поверхности. Распространением потенциала обусловлено возникновение так называемых локальных токов, циркулирующих между возбужденным и невозбужденными участками мембраны. В состоянии покоя внешняя поверхность клеточной мембраны имеет положительный потенциал, а внутренняя — отрицательный. В момент возбуждения полярность мембраны изменяется на обратную: ее внешняя поверхность заряжена отрицательно по отношению к внутренней. В результате этого между возбужденными и не возбужденными участками мембраны имеется разность потенциалов. Наличие разности потенциалов приводит к появлению между этим участками электрических токов, названным локальными токами или токами действия.
На поверхности клетки локальный ток течет от невозбужденного участка к возбужденному; внутри клетки он течет в обратном направлении. Локальный ток, как и любой электрический ток, оказывает раздражающее действие на соседние невозбужденные участки и вызывает увеличение проницаемости их мембран. Это приводит к снижению в них потенциала покоя. Когда деполяризация достигает критического значения, в этих участках возникают потенциалы действия, а в том участке, который ранее был возбужденным, в это время уже происходят восстановительные процессы реполяризации. Вновь возбужденный участок в свою очередь становится электроотрицательным и возникающий локальный ток раз
дражает следующий за ним участок. Этот процесс многократно повторяется и обуславливает распространение импульсов возбужде
ния по всей длине клетки в обоих направлениях (рис. 43) [12].
распространение нервного импульса
Рис. 44. Распространение нервного импульса вдоль нервного волокна [8]
Под влиянием локальных токов волна возбуждения распространяется вдоль волокна без затухания (бездекрементое проведение). Это обусловлено тем, что локальные токи только деполяризуют мембрану до критического уровня, а потенциалы действия в каждом участке мембраны поддерживаются независимыми ионными токами перпендикулярными к направлению распространения возбуждения [12].
Живые существа жизненно заинтересованы в высокой скорости проведения нервного импульса [6]. Скорость проведения возрастает с увеличением диаметра волокна. Это объясняется тем что, с увеличением диаметра уменьшается сопротивление, приходящееся на единицу длины волокна [12]. Головоногие моллюски пошли по пути увеличения радиуса нервного волокна, создав гигантские аксоны. Позвоночные “изобрели” миелиновое волокно (рис. 44) [6].
Ядро шванновской клетки
Рис. 45. Структура миелинизированного нервного волокна [15]
Миелин содержит много холестерина и мало белка; его удельное сопротивление выше удельного сопротивления других биологических мембран [6]. В электрическом отношении миелин является изолятором; его удельное сопротивление в 10 6 раз превышает удельное сопротивление раствора Рингера. В результате этого локальные токи через миелиновые оболочки протекать не могут; они циркулируют между перехватами Ранвье. При возбуждении одного перехвата Ранвье между ним и следующим перехватом возникают локальные токи, и импульс как бы перескакивает на второй перехват, со второго на третий и так далее. Такой способ передачи проведения нервного импульса называется сальтаторным. В результате сальтаторного способа передачи нервного импульса скорость распространения нервного импульса в миелинизированном волокне в 10 раз выше, чем не миелинизированных волокнах. Помимо этого, сальтаторный способ передачи возбуждения является более экономичным, поскольку в этом случае ионные потоки проходят не через всю поверхность мембраны клетки, как при непрерывном распространении, а только через поверхность мембраны в области перехватов Ранвье [12].
Рис. 46. Схема сальтаторного проведения импульса [14]
Высокая скорость распространения импульса — не единственное существенное требование к качеству нервных проводников. Отметим, что скорость динамики потенциала во времени определяет длительность рефрактерного периода: чем медленнее изменяется потенциал, тем больше продолжительность одного импульса и тем ниже максимальная частота следования импульсов по волокну.
В межперехватном промежутке, покрытом миелиновой оболочкой, удельное сопротивление мембраны в сотни и тысячи раз больше, чем в зоне перехвата Ранвье, поэтому постоянная времени должна быть большой и соответственно должна быть большой рефрактерность. Тем не менее благодаря тому, что миелиновая оболочка представляет собой дупликатуру мембраны, многократно «обматывающую» нервное волокно, емкости каждого витка мембраны соединяются последовательно, и общая емкость в «п» раз меньше емкости одного слоя мембраны. Большое удельное сопротивление и малая емкость компенсируют друг друга, и в итоге постоянная времени миелинизированных волокон составляет 1 мс.
Важно заметить, что огромное значение имеет не только материал оболочки (высокое сопротивление), но и его пространственная организация. Именно «геометрия» миелизированной оболочки обеспечивает максимальное значение постоянной длины при минимальной постоянной времени из всех возможных соотношений емкости и проводимости. В результате по миелиновым волокнам обеспечивается как высокая скорость проведения импульсов, так и высокая плотность передачи информации, тогда как по немиелинизированным волокнам потенциал распространяется со значительным затуханием и с малой скоростью [11].
При генерации нервного импульса в нерве происходят тепловые явления — сначала он нагревается, потом охлаждается. Было установлено, что этот эффект определяется тремя слагаемыми. Во-первых, во время генерации потенциала действия происходит диссипация энергии, вызванная потоками ионов. Во-вторых, в то же время происходит диссипация вследствие изменения разделенных зарядов на двух сторонах мембраны — понижение трансмембранного потенциала отвечает выделению тепла. Это вклад, однако, на порядок меньше ионного. Наконец, переход ионного канала из закрытого состояния в открытое состояние сопровождается выделением тепла, далее поглощаемого. Теория в общем согласуется с опытом, который дает для вагуса кролика выделение тепла, равное 100 мкДж/г, и последующее поглощение — 93 мкДж/г на импульс [14].
Передача возбуждения с одной нервной клетки на другую и с нервной клетки на эффекторный элемент осуществляется специальными образованиями — синапсами, которые являются функциональными контактами между двумя клетками. Нервное окончание входящее в состав синапса, утолщено и обычно имеет вид бляшки. Мембрана на конце волокна, с которого передается возбуждение называется пресинаптической. Мембрана другой клетки, на которую передается возбуждение, называется постсинаптической. Пространство между пресинаптической и постсинаптической мембранами, называют синаптической щелью, имеет ширину 20-30 нм. Оно заполнено межклеточной жидкостью [12].
Передача возбуждения в синапсах может происходить двумя способами: электрическим и химическим. Электрическая передача возбуждения заключается в том, что потенциал действия на пресинаптической мембране служит раздражителем для постсинаптической мембраны. Чтобы эта передача могла осуществляться, синапсы должны иметь сравнительно большую площадь контакта. Кроме того, при таком способе передачи пресинаптическая и постсинаптическая мембраны обычно сближены и даже могут соприкасаться. Передача возбуждения электрическим путем встречается редко и в основном у низших животных: кишечнополостных, червей, ракообразных. Электрическая передача возбуждения наблюдается в гладких мышцах и мышце сердца [12].
Химическая передача возбуждения осуществляется с помощью особых биологически активных веществ — медиаторов, из которых наиболее известны ацетилхолин и норадреналин. Медиаторы содержатся в синаптических пузырьках, локализованных в пресина-тическом окончании. Когда на пресинаптическом волокне возникает потенциал действия, медиатор выходит в синаптическую щель и диффундирует к постсинаптической мембране, обладающей высокой чувствительностью к нему. Под влиянием медиатора изменяется проницаемость мембраны для ионов натрия и калия. Это изменение мембранного потенциала называют возбуждающим постсинаптическим потенциалом [12].
Постсинаптические потенциалы имеют сравнительно небольшую продолжительность, поскольку медиатор быстро расщепляется соответствующим ферментом, и не распространяются по клетке.
Катцем было установлено два важных отличия свойств постсинаптической мембраны и других участков клетки. Во-первых, постсинаптическая мембрана под действием медиатора становится одинаково проницаема для натрия и калия. Поэтому постсинаптический потенциал не превышает потенциал покоя. Во-вторых, проницаемость постсинаптической мембраны не является функцией мембранного потенциала и, следовательно, постсинаптический потенциал не подчиняется закону «все или ничего». Величина постсинаптического потенциала пропорциональна количеству поступившего медиатора. Когда постсинаптический потенциал достигает определенной величины, то в соседних с синапсом участках мембраны генерируются потенциалы действия, передающие возбуждение по клетке [12].
Частота появления потенциалов действия пропорциональна величине постсинаптического (генераторного) потенциала [12].
Существование стадии постсинаптических потенциалов является одним из условий трансформации ритма в синапсах [12].
Кроме возбуждающих синапсов, вызывающих деполяризацию мембраны, в нервной системе существуют тормозные синапсы, которые при активации вызывают гиперполяризацию мембраны и понижение активности клетки. Эта гиперполризация обычно обозначается как тормозной постсинаптический потенциал [12].
Дж. Экклс в 1964 году показал, что в тормозных синапсах медиатор открывает в постсинаптичекой мембране поры, проницаемые для ионов К + и СГ. Диффузия этих ионов приводит к гиперполяризации мембраны и к торможению клеток [12].
Выделение небольших порций ацетилхолина происходит и в покое, независимо от нервного импульса. Импульс очень сильно повышает эту активность за время порядка 1 мс. Спонтанная нейросекреция не обусловлена утечкой ацетилхолина из окончаний путем случайной диффузии. Спонтанная нейросекреция есть квантовое освобождение ацетилхолина, при котором порции ацетилхолина выделятся в случайные моменты времени по типу “все или ничего” из дискретных точек концевой мембраны аксона. Величина кванта ацетилхолина не зависит от изменений мембраны, связанных с нервным импульсом. Импульс изменяет в сотни тысяч раз вероятность выделения кванта. Потенциал постсинаптической мембраны, возникающий под влиянием нервного импульса, слагается из большого числа “миниатюрных потенциалов”, создаваемых отдельными порциями кванта ацетилхолина. Число “квантов”, участвующих в реакции в одном мионевральном соединении, зависит от присутствия ионов Са 2+ и Mg 2+ : Са 2+ стимулирует секрецию ацетилхолина, Mg 2+ ее ингибирует [14].
💡 Видео
Урок 269. Задачи на тепловое действие токаСкачать

Физика - уравнения равноускоренного движенияСкачать

Уравнение равномерного движения. Решение задач по теме.Скачать

3 14 Уравнения МаксвеллаСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Видеоурок "Общие уравнения прямой"Скачать

#70. НЕОЖИДАННОЕ уравнение в №13 ЕГЭ по математикеСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Эллиптические уравнения. ТеорияСкачать

Билет №34 "Электромагнитные волны"Скачать

§9 Уравнение прямой в отрезкахСкачать
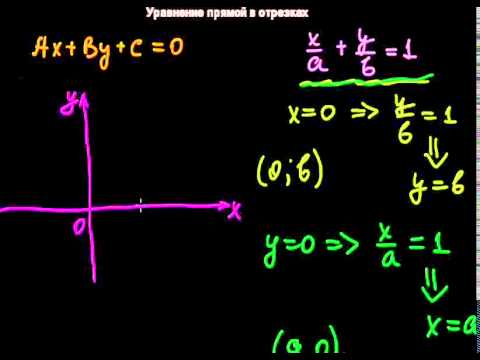
Уравнение прямой.Скачать

10. Волновое уравнение на отрезке. Сложные задачиСкачать




























